ベクトル（数学）とは何ですか? -マソリティ

このページでは、ベクトルとは何か、その特徴、計算方法、ベクトルを使った演算の方法、存在するさまざまなタイプなど、ベクトルに関するすべてを説明します。

ベクトルとは何ですか?

ベクトルの数学的定義は次のとおりです。

数学では、ベクトルは、ある点 (原点と呼ばれる) から別の点 (終点と呼ばれる) に向かう有向線分です。

たとえば、以下のグラフでは、ベクトルが

$\vv{AB}$

始点として点 A があり、終点として点 B があります。

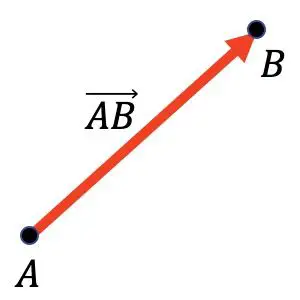
ベクトルは主に数学、特に幾何学や物理学でベクトル力をグラフィックで表すために使用されます。

ベクトルの特徴

ベクトルの数学的意味が何であるかを理解したら、次にその特性が何であるかを見てみましょう。

各ベクトルには次の幾何学的特徴があります。

方向: ベクトルの方向は、ベクトルを含む線、またはそれに平行な線の方向です。言い換えれば、ベクトルの方向は、そのベクトルが乗っている直線になります。
方向: ベクトルの方向は、矢印で示される当該ベクトルの方向です。
モジュール(または大きさ): ベクトルのモジュールはその長さであり、ベクトルの数値に対応します。したがって、ベクトルが大きいほど、それが表すベクトル量も大きくなります。
適用点: ベクトルの適用点は、そのベクトルの原点です。

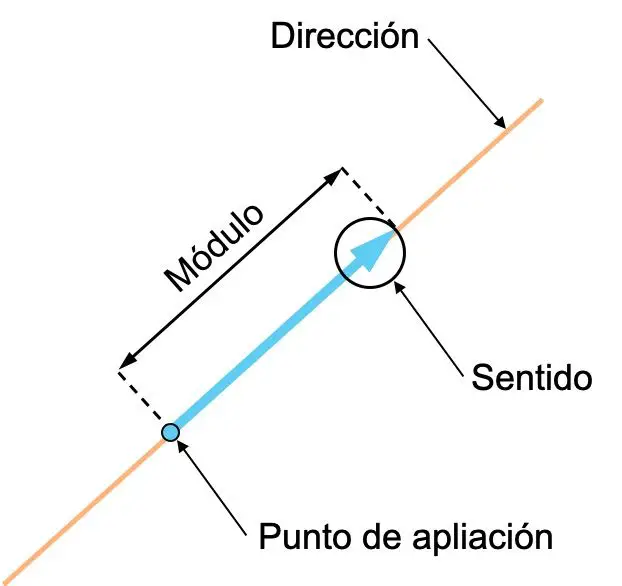
方向とベクトルの方向の概念は混同されやすいため、両者の違いを区別することが重要です。 2 つのベクトルを含む次の例を見てください。どちらも方向は同じですが、意味が異なります。

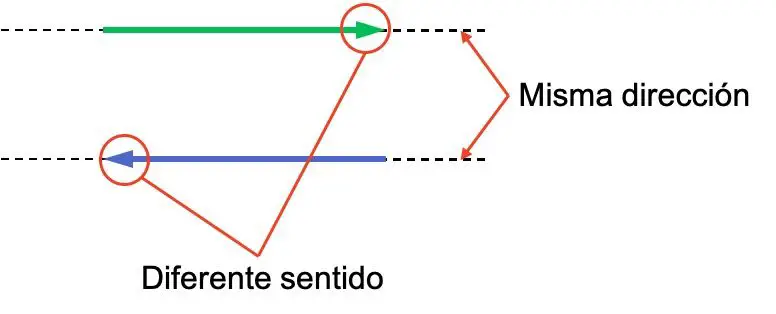
2 つのベクトルは平行であるため、同じ方向になります。代わりに、それらは後ろを向いているため、方向が逆になります。

ベクトルの構成要素

ベクトルが矢印によってグラフィカルに表現されることを見てきましたが、ベクトルはベクトルの成分 (または座標) によって数値的に表現することもできます。

たとえば、次のベクトルがグラフで表されているとします。

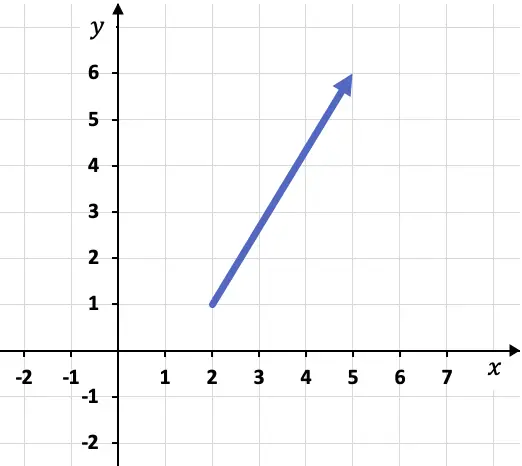
ベクトルの成分を計算するには、まずベクトルの始点と終点の座標、つまり始点と終点の座標を特定する必要があります。この場合、ベクトルの始点と終点は次のとおりです。

ベクトルの原点: A(2,1)

ベクトルの終点: B(5,6)

したがって、ベクトルの座標または成分を見つけるには、終点から原点を引くだけです。

$\begin{aligned} \vv{AB} & = B- A \\[2ex] & = (5,6)- (2,1) \\[2ex] &= (5-2 \ , \ 6-1) \\[2ex] &= (3,5) \end{aligned}$

したがって、グラフで表されるベクトルの成分は次のようになります。

$\vv{\bm{AB}}\bm{=(3,5)}$

ベクトル演算

ベクトルの追加

2 つのベクトルを数値的に加算するには、それぞれのコンポーネントを加算する必要があります。言い換えると、2 つのベクトルの X 座標は加算され、Y 座標と同じになります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y) \end{array} \end{empheq}$

これがどのように行われるかを確認できるように、次の 2 つのベクトルを追加します。

$\vv{\text{u}} = (2,3) \qquad \vv{\text{v}}=(4, -1)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(2,3) +(4,-1) \\[2ex] & = (2+4,3+(-1)) \\[2ex] & = \bm{(6,2)} \end{aligned}$

2 つのベクトルをグラフィック表示から追加することもできます。これには通常、平行四辺形の法則が使用されますが、さまざまな方法があります。ここでは、 2 つのベクトルをグラフィカルに追加する方法の例と解決された演習を参照できます。

ベクトル減算

2 つのベクトルを解析的に減算するには、それぞれの成分を減算する必要があります。つまり、2 つのベクトルの X 座標は互いに減算され、Y 座標と同じになります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c} \vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)\\[4ex]\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y) \end{array} \end{empheq}$

例として、次の 2 つのベクトルを減算します。

$\vv{\text{u}} = (3,1) \qquad \vv{\text{v}}=(2, -4)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(3,1) -(2,-4) \\[2ex] & = (3-2,1-(-4)) \\[2ex]& = (3-2,1+4) \\[2ex] & = \bm{(1,5)} \end{aligned}$

加算と同様に、2 つのベクトルの表現を使用して減算することもできます。このためには、通常は三角定規が使用されますが、いくつかの方法があります。これらすべてを例と、 2 つのベクトルをグラフィカルに減算する方法に関する解決済み演習で確認できます。

ベクトルのモジュール

このページの最初で見たように、ベクトルの大きさはそのベクトルの長さに対応します。ベクトルの長さ (または大きさ) は、その成分から決定できます。

任意のベクトルを考えてみましょう。

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

平面内のベクトルの大きさを求めるには、次の公式を適用する必要があります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2} \end{empheq}$

たとえば、次の式を使用して次のベクトルの大きさを計算します。

$\vv{\text{u}} = (3,-4)$

$\lvert \vv{\text{u}} \rvert =\sqrt{3^2+(-4)^2} = \sqrt{9+16}=\sqrt{25} = \bm{5}$

非常に単純そうに見えますが、ベクトルの大きさの決定は複雑になる場合があります。さらに多くの例を確認し、ベクトルのモジュールの解決された演習で練習したい場合は、このリンクされたページにアクセスすることをお勧めします。

ベクトルとスカラーの乗算

ベクトルと数値 (またはスカラー) の積を数値的に計算するには、ベクトルの各成分にその数値を乗算する必要があります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}\vv{\text{u}} = (\text{u}_x,\text{u}_y)\\[4ex]k\cdot \vv{\text{u}} =(k\cdot \text{u}_x \ , \ k\cdot \text{u}_y) \end{array} \end{empheq}$

次の一般的な例では、スカラーの符号に関係なくベクトルの方向がどのように維持されるかを確認できます。一方、ベクトルの方向は、ベクトルに乗算する数値の符号に依存します。

以下に、ベクトルと数値の積を求める方法の数値例を示します。

$\vv{\text{u}} =(3,-2)$

$4\cdot \vv{\text{u}} =(4 \cdot 3 \ , \ 4 \cdot (-2)) = \bm{(12,-8)}$

スカラー積

解析幾何学におけるドット積は、2 つのベクトルを乗算して実数に変換するベクトル演算です。

したがって、2 つのベクトルの内積の式は次のようになります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \cdot \vv{\text{v}} = \text{u}_x\cdot \text{v}_x + \text{u}_y\cdot \text{v}_y \end{empheq}$

以下に、2 つのベクトル間の内積の結果を計算する例を示します。

$\vv{\text{u}} = (4,2) \qquad \vv{\text{v}} = (-1,3)$

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(4,2)\cdot (-1,3) \\[1.5ex]&=4\cdot (-1) + 2 \cdot 3 \\[1.5ex] & = -4+6 \\[1.5ex] & =\bm{10} \end{aligned}$

このリンクでは、ドット積の他の例を参照できます。さらに、2 つのベクトル間の内積を求める別の方法、ベクトルを使用したこのタイプの演算の特性、および段階的に解決される演習も見つかります。

ベクトル積

名前はよく似ていますが、内積と外積はまったく異なります。

外積(外積とも呼ばれる) は、空間 (R3) 内の 2 つのベクトル、つまり 3 座標ベクトル間の演算です。

したがって、2 つの 3 次元ベクトルがあるとします。

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

2 つのベクトルの外積は、次の 3×3 行列式の結果と等しくなります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix} \end{empheq}$

ここでベクトルは

$\vv{i}, \vv{j},\vv{k}$

は、それぞれ X、Y、Z 軸方向の単位ベクトルです。

さらに、結果のベクトルの方向は、乗算された 2 つのベクトルに対して垂直になります。

ご想像のとおり、このタイプの演算を解決するのはこれまでの演算よりも難しいため、2 つのベクトル間の外積がどのように計算されるかについての詳細な説明を 1 ページ全体に用意しました。したがって、興味がある場合は、アクセスして、解決されたベクトル積演習で練習することをお勧めします。

混合製品

3 つのベクトルの混合積(トリプルドット積とも呼ばれます) は、ドット積とベクトル積という 2 つの異なるタイプの演算を含む 3 つのベクトル間の連続乗算です。したがって、2 つのベクトル演算を組み合わせるとスカラー (実数) が得られます。

具体的には、混合積は 2 つのベクトルのベクトル積を計算し、その後、得られた結果に 3 番目のベクトルをベクトル乗算することで構成されます。式を見てください。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.3pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white,shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}}) \end{empheq}$

ベクトル積と同様に、ベクトル間の混合積を解くのは簡単ではありません。このため、 3 つのベクトルの混合積に関するこの説明を参照することをお勧めします。この説明には、例、解決済みの演習、およびこのベクトル演算の幾何学的意味が含まれています。

ベクトル型

ベクトルにはさまざまな種類がありますが、知っておくべき最も重要な定義は次のとおりです。

単位ベクトル: モジュールが 1 に等しいベクトル。
固定ベクトル: ベクトルの原点を固定点に適用すると、ベクトルは固定されます。
自由ベクトル: ベクトルは、適用点が定義されていない場合は自由ですが、自由点です。
同一直線上にあるベクトル: 2 つ以上のベクトルが同じ作用線 (ベクトルが位置する直線) を共有する場合、それらのベクトルは同一直線上にあります。
等価ベクトル: 2 つのベクトルが同じサイズ、同じ意味、同じ方向を持っている場合、それらのベクトルは等花粉です (ただし、適用点が異なる場合があります)。
連結ベクトル: 連結ベクトルは、同じ線上で作用する等花粉ベクトルです。
反対のベクトル: 2 つのベクトルは、大きさと方向が同じで方向が異なる場合、反対になります。
位置ベクトル: 位置ベクトルは、点 (0,0) (座標の原点) を原点とするベクトルです。
競合するベクトル: 2 つ以上のベクトルは、その作用線が同じ点を通過する、つまり交差するときに同時に存在します。
平行ベクトル: 2 つ以上のベクトルは、その方向に関係なく、同じ方向であれば平行です。
垂直ベクトル: 2 つのベクトルの方向が 90 度の角度を形成する場合、2 つのベクトルは垂直 (または直交) になります。
正規直交ベクトル: 2 つ以上のベクトルが互いに垂直であり、さらにユニタリである (大きさが 1 に等しい) 場合、それらのベクトルは正規直交です。
同一平面上にあるベクトル: 2 つ以上のベクトルが同じ平面内に含まれる場合、同一平面上にあります。

2 つのベクトル間の角度

指定された 2 つのベクトルの間の角度を見つけるには、次の公式を適用する必要があります。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.4pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cos(\alpha) =\cfrac{\vv{\text{u}} \cdot \vv{\text{v}}}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert} \end{empheq}$

金

$\lvert \vv{\text{u}} \rvert$

そして

$\lvert \vv{\text{v}} \rvert$

ベクトルのモジュールです

$\vv{\text{u}}$

そして

$\vv{\text{v}}$

それぞれ。