このページでは、平面とは何か、平面の計算方法、およびそのすべてのプロパティについて説明します。さらに、平面の例、2 つの平面間の相対位置、2 つの平面間の角度を決定する方法、そして最後に、平面方程式を使用して任意の平面を数値で表現する方法を確認できます。
計画とは何ですか?
解析幾何学における平面の定義は次のとおりです。
平面は、2 つの次元 (長さと幅) を持つ幾何学的オブジェクトです。
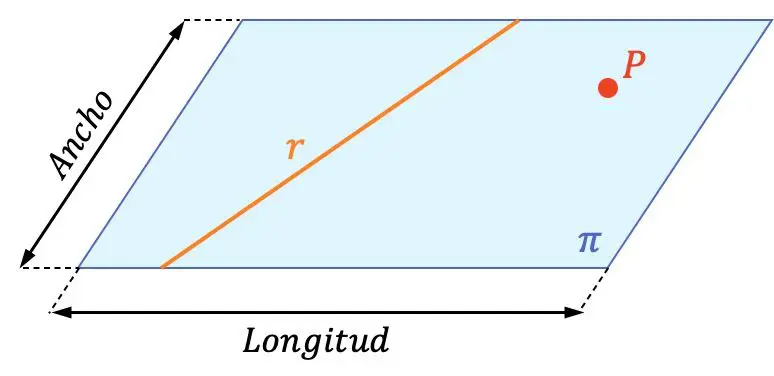
したがって、平面には無限の線と無限の点が含まれます。上のグラフ表示では、平面、線、点の違いがわかります。次の行を確認することもできます。
![]()
そして先端
![]()
飛行機の中に含まれている
![]()
グラフ化された計画からわかるように、計画には通常ギリシャ文字で名前が付けられます。
![]()
数学でよく使用される平面の例は、デカルト平面です。デカルト平面は、横軸 (X 軸) と縦軸 (Y 軸) によって定義される平面です。デカルト平面の用途の 1 つは、基準系内のオブジェクトの位置を記述するために使用されることです。
計画を立てる
平面の意味を理解したので、3 次元空間 (R3) 内の任意の平面をどのように決定できるかを見てみましょう。
計画は、次の幾何学的要素によって完全に決定されます。
- 3つの点が揃っていません。
- 直線と外側の点。
- 2 本の平行な線、または 2 本の交差する線。
最後の点については、2 本の線が平行であることが何を意味するかはおそらくすでにご存知でしょう。ただし、割線の意味はあまり知られていないため、質問がある場合は、 「割線とは」を参照してください。
したがって、上記の 3 つの条件のいずれかが満たされていれば、計画を立てることができます。
プランのプロパティ
この計画は次の特性を満たしています。
- 平面には無数の点が含まれます。
- 平面には無限の線が含まれています。
- 平面は無限です。つまり、それは空間に無制限に広がる面です。
- 2 つの交差する平面によって線が決まります。
- 平面内に点を持つ線は、必ずしもそこに含まれるとは限りません。線が平面の一部であるためには、その平面内に少なくとも 2 つの点がなければなりません。
- 無限の平面が直線を横切ります。
- 半平面とは、平面を線の 1 つで切断したときに分割される 2 つの部分のそれぞれです。
平面方程式
解析幾何学において、平面の方程式は、任意の平面を数学的に表現できる方程式です。したがって、平面の方程式を見つけるには、1 つの点と、その平面に属する 2 つの線形に独立したベクトルのみが必要です。

ただし、上記の計画の概念の説明で見たように、計画を決定するにはいくつかの方法があります。まあ、同じように、計画を分析的に表現するにもさまざまな方法があります。
したがって、平面のすべてのタイプの方程式は、平面のベクトル方程式、パラメトリック方程式、陰的 (または一般) 方程式、および平面の正準 (または部分) 方程式です。
次に、計画のすべての方程式の説明と公式を詳しく見ていきます。
平面のベクトル方程式
点と平面の 2 つの方向ベクトルを考えてみましょう。
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面のベクトル方程式の公式は次のとおりです。
![]()
または同等のもの:
![]()
金
![]()
そして
![]()
は 2 つのスカラー、つまり 2 つの実数です。
平面のパラメトリック方程式
平面のパラメトリック方程式の公式は次のとおりです。
![]()
金:
-
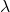
そして
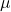
は 2 つのスカラー、つまり 2 つの実数です。
-
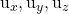
計画の 2 つの誘導ベクトルのうちの 1 つのコンポーネントです
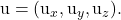
-
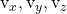
計画の他の方向ベクトルの構成要素です
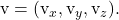
平面の暗黙的または一般方程式
点と平面の 2 つの方向ベクトルを考えてみましょう。
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面の陰的な一般方程式またはデカルト方程式は、次の行列式を解き、結果を 0 に設定することによって取得されます。
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
したがって、結果として得られる計画の暗黙的な方程式または一般方程式は次のようになります。
![]()
このタイプの平面方程式は、デカルト平面方程式とも呼ばれます。
平面の正準方程式または部分方程式
平面の正準方程式または部分方程式の式は次のとおりです。
![]()
金:
-

は平面と X 軸の交点です。
-

は平面と Y 軸の交点です。
-

これは、平面が Z 軸と交差する場所です。
平面の正準方程式 (または部分方程式) は、その一般方程式から取得することもできます。
![]()
まず、次の方程式から係数 D を解きます。
![]()
次に、計画の方程式全体をパラメーター D の値で除算し、符号を変更します。
![]()
![]()
そして、分数の性質を利用すると、次の式が得られます。
![]()
したがって、この式から、平面の正準方程式または部分方程式の項を直接計算できる式を導き出します。
![]()
したがって、計画の方程式のこの変形を形成できるようにするには、係数 A、B、および C がゼロ以外でなければならず、これにより分数の不確定性が回避されます。
2 つの平面の相対位置
解析幾何学では、2 つの平面間に可能な相対位置は、割線平面、平行平面、一致平面の 3 つだけです。
- 交差する平面: 2 つの平面が 1 つの線上でのみ交差する場合、2 つの平面は交差しています。
- 平行平面: 2 つの平面は、どの点でも交差しなければ平行です。
- 一致する平面: 2 つの平面がすべて共通点を持つ場合、それらの平面は一致します。
交差する平面

平行面

一致する平面

さらに、2 つの交差する平面が 90 度の角度で交差する場合、それらは 2 つの相互に垂直な平面になります。
2 つの平面間の角度
2つの平面間の角度は、前記平面の法線ベクトルによって形成される角度に等しい。したがって、 2 つの平面間の角度を求めるには、それらの法線ベクトルが等しいため、それらの法線ベクトルによって形成される角度が計算されます。
したがって、2 つの平面間の角度がどのようなものであるかを正確に理解したら、空間内の 2 つの平面間の角度を計算する公式を見てみましょう。これは、2 つのベクトル間の角度の公式から推定されます。
2 つの異なる平面の一般 (または暗黙の) 方程式を考えると、次のようになります。
![]()
![]()
各平面の法線ベクトルは次のとおりです。
![]()
![]()
これら 2 つの平面によって形成される角度は、次の式を使用して法線ベクトルによって形成される角度を計算することによって決定されます。
![]()
明らかに、公式から 2 つの平面によって形成される角度の余弦を計算したら、その角度の値を見つけるために余弦を反転する必要があります。
一方、2 つの平面が垂直または平行である場合は、2 つの平面間の角度を直接決定できるため、次の式を適用する必要はありません。
- 2 つの平行な平面間の角度は、それらの法線ベクトルが同じ方向を持っているため 0° です。
- 2 つの垂直な平面間の角度は 90 度です。これは、それらの法線ベクトルも互いに垂直 (または直交) しており、したがって直角を形成するためです。