ここでは、対称方程式とも呼ばれる、直線の正準 (または部分) 方程式の公式が何であるかについて説明します。さらに、例題を見て、解決された演習で練習することができます。さらに、直線の一般 (または暗黙の) 方程式から正準方程式がどのように計算されるかもわかります。
直線の正準方程式または部分方程式は何ですか?
線の数学的定義は、曲線や角度を持たずに同じ方向に表現される一連の連続する点であることに注意してください。
したがって、線 の正準方程式は、線 の部分方程式とも呼ばれ、任意の線を数学的に表現する方法です。これを行うには、前記線の座標軸との交点を知るだけで十分です。
一方、解析幾何学では、直線の正準方程式(または部分方程式)は、直線の対称方程式とも呼ばれます。
直線の正準方程式または部分方程式の式
直線の正準方程式または部分方程式は、直線が x 軸および y 軸と交差する位置の値を知ることで決定できる直線の代数式です。
線が次の点でデカルト軸と交差する場合:
X 軸との交点:
![]()
Y 軸との交点:
![]()
直線の正準 (または部分) 方程式の式は次のとおりです。
![]()

次の 3 つの場合のいずれにおいても、直線の正準 (または部分) 方程式が存在しないことに注意してください。
- 線が垂直、つまり OY 軸に平行の場合。なぜなら、垂直線の方程式は

- 線が水平、つまり OX 軸に平行の場合。なぜなら水平線の方程式は

- 直線が座標原点(点)を通過するとき
)、直線の方程式には 2 つの不確定要素が存在することになるためです。
直線の正準方程式または部分方程式を見つける方法の例
概念をよりよく理解するために、直線の部分 (または正準) 方程式の問題を解きます。
- 次の 2 点を通過する直線の正準方程式または部分方程式を求めます。
![]()
この場合、宣言では 2 点が与えられるのではなく、軸との 2 つの交点が与えられます。
線と X 軸の交点:
![]()
線と Y 軸の交点:
![]()
したがって、軸との 2 つの交点はすでにわかっているので、直線の正準方程式または部分方程式の公式を適用するだけです。
![]()
最後に、パラメータの値を代入します。
![]()
そして
![]()
式の中で:
![]()
これで、直線の正準 (または部分) 方程式が何であるかがわかりました。ただし、線を表現する方法は他にもあり、その中でも明示的な方程式が際立っていることを知っておく必要があります。この種の直線方程式は完全に理解するのが難しいため、リンク先のページで詳しく説明しています。
一般方程式から直線の正準方程式または部分方程式を計算します。
直線の正準方程式または部分方程式を決定する方法を説明しましたが、他の方法もあります。
直線の正準方程式または部分方程式は、この同じ直線の一般 (または陰的) 方程式から取得できます。
![]()
まず、係数 C でサイドを変更します。
![]()
次に、方程式全体を符号を変更したパラメーター C の値で除算します。
![]()
![]()
そして、分数の性質を通じて、直線の正準方程式または部分方程式の公式に到達します。
![]()
したがって、この式から次のことがわかります。
![]()
そして
![]()
直線の正準方程式の は次の式と等価です。
![]()
直線の正準方程式または部分方程式の問題を解決しました
演習 1
次の直線の座標軸との交点は何でしょうか?
![]()
練習問題の直線は、直線の正準方程式または部分方程式の形式で表されます。その式は次のとおりです。
![]()
したがって、線が座標軸と交差する点は次のようになります。
X 軸との交点:
![]()
Y 軸との交点:
![]()
演習 2
グラフの線の正準方程式または部分方程式は何ですか?
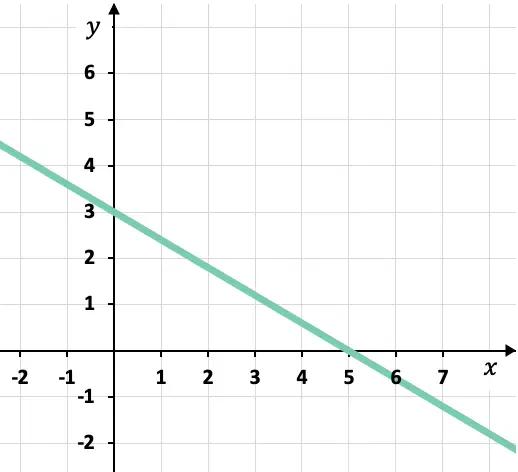
グラフから、線が座標軸と交差する点を知ることができます。
線と X 軸の交点:
![]()
線と Y 軸の交点:
![]()
したがって、軸との 2 つの交点がすでにわかっている場合は、直線の正準方程式または部分方程式の公式を使用するだけです。
![]()
最後に、パラメータの値を代入します。
![]()
そして
![]()
式の中で:
![]()
演習 3
次の一般 (または陰的) 方程式によって決定される直線の正準方程式または部分方程式を計算します。
![]()
一般方程式から部分方程式に移行するには、まず方程式の独立項を分離する必要があります。
![]()
![]()
次に、方程式全体を方程式の右側の係数で割ります。
![]()
![]()
上記の式は次と同等です。
![]()
したがって、直線の正準方程式、部分方程式、または対称方程式は次のようになります。
![]()
演習 4
方向ベクトルが次のような正準方程式または部分方程式を決定します。
![]()
そしてポイントを通過します
![]()
まず、直線の方向ベクトルと直線に属する点から直線の連続方程式を簡単に見つけます。
![]()
![]()
![]()
次に、分数を横に乗算し、結果の項をグループ化して、直線の一般方程式を計算しましょう。
![]()
![]()
![]()
![]()
したがって、直線の一般方程式を正準方程式に変換するだけで十分です。これを行うには、まず方程式から独立項を削除します。
![]()
次に、方程式全体を方程式の右側の係数で割ります。
![]()
![]()
上記の式は次と同等です。
![]()
負を負で割ると正と等しくなります。
![]()
分数はこれ以上単純化できないため、直線の正準方程式、部分方程式、または対称方程式は次のようになります。
![]()