このページでは、空間内の 2 つの線の間の距離が (R3 で) 計算される方法がわかります。その種類 (平行線、割線、一致線、割線、垂直線など) に関係ありません。さらに、例題や演習を段階的に解くことができます。
2本の線の間の距離を計算する方法
2 つの線の間の距離は、一方の線上の任意の点ともう一方の線上の任意の点の間の最小距離です。この距離は、一方の線からもう一方の線までの、同時に両方の線に垂直な線分の長さに対応します。
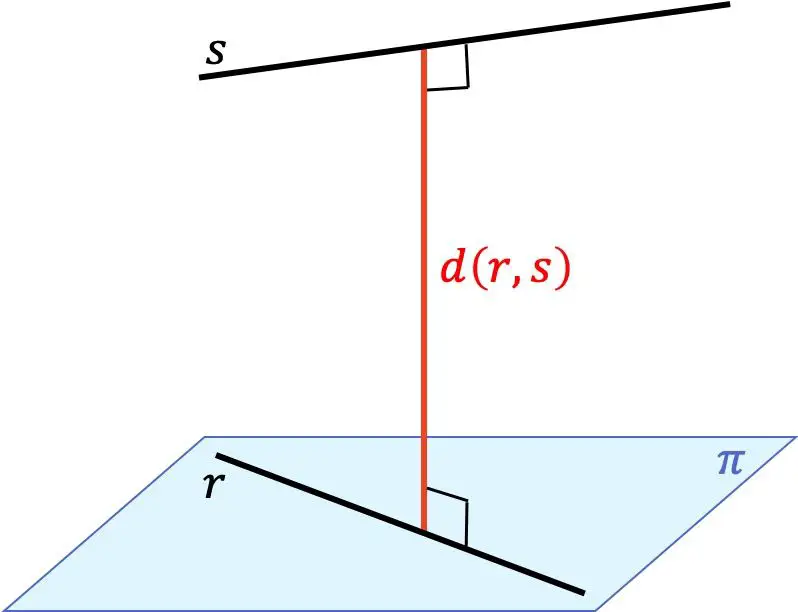
したがって、3 次元 (3D) 空間内の 2 つの異なる線の間の距離を見つけることは、それらの間の相対位置に依存します。
- 2 つの線が一致するか交差する場合、2 つの線は (少なくとも) 1 点で交差するため、2 つの線の間の距離はゼロになります。
- 2 本の線が平行の場合、一方の線上の任意の点を取得し、その点ともう一方の線の間の距離を計算する必要があります (これを行う方法の例を以下に示します)。
- 2 本の線が空間内で交差する場合、交差する 2 本の線間の距離の公式を適用する必要があります (詳細については以下を参照)。
したがって、2 つの線の間の距離を計算するには、まずそれらの線がどのような種類であるかを知り、場合に応じて何らかの式を使用する必要があります。したがって、続行する前に、空間内の 2 つの線の相対位置を見つける方法をすでにマスターしていることが重要ですが、それがどのように行われたかを覚えていない場合でも、リンクで非常に完全な説明と例と演習が表示されます。一歩ずつ。
空間内の 2 本の平行線の間の距離を見つける方法
空間 (R3) における 2 本の平行線の間の距離の計算は、平面 (R2) での場合と同じ方法で行われます。2本の線のいずれか上の点を取得し、もう一方の線上でこの点の距離を見つける必要があります。ライン。

したがって、3 次元の点から線までの距離を計算する式 (2 本の平行線の間の距離を決定するために使用されます) は次のとおりです。
![]()
金:
-

線の方向ベクトルの大きさです

-

線上の点です


線上の点

そして

2 つの点によって定義されるベクトル
-

ベクトル間の外積の大きさです

そして

例として、空間内の 2 本の平行線間の距離の問題を解決します。
- 次の 2 本の平行線の間の距離はいくらですか?
![]()
![]()
両方の直線はベクトル方程式の形式で表現されるため、それぞれの方向ベクトルと点を簡単に見つけることができます。
![Rendered by QuickLaTeX.com \displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91c721e906a848c6c129721fe7908112_l3.png)
方向ベクトルと直線の点の求め方に疑問がある場合は、 直線の方程式の説明を参照することをお勧めします。そこでは、直線のすべての方程式について説明しました。方向ベクトルと直線に属する点の検索は、直線が表現される方程式の種類に依存するためです。
ここで、2 本の平行線間の距離を求めるには、点から線までの距離の公式を適用する必要があります。
![]()
したがって、一方では、ベクトル積から得られるベクトルのモジュールを計算します。計算方法に疑問がある場合は、 ベクトル積の公式を参照してください。さらに、ベクトル間のこの演算の例と解答済みの演習も表示されます。
![]()
![Rendered by QuickLaTeX.com \vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f166cb84d794adae8b8e5678790a5ad8_l3.png)
![]()
そして、一方で、直線のベクトルの大きさを求めます。
![]()
![]()
最後に、各項の値を式に代入し、線間の距離を計算します。
![]()
したがって、2 つの線の間の距離は 3.60 単位です。
空間内で交差する 2 本の線の間の距離を決定する方法
最初に見たように、交差する 2 つの線の間の距離を求める方法は、平行な線の間の距離を求める手順とは異なります。

したがって、空間内で交差する 2 つの線の間の距離を決定する方法はいくつかあります。このページでは、最も単純な 1 つの手順のみを説明します。他の 2 つの方法は長くて複雑で、実際には実際には使用されないためです。
方向ベクトルと 2 つの交差する線の任意の点を次のようにします。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-569f8d554a0f3704d247862d0b8ef852_l3.png)
交差する 2 本の線の間の距離の公式は次のとおりです。
![]()
金
![]()
ベクトルの混合積の絶対値です。
![]()
および点によって定義されるベクトル
![]()
そして
![]()
。そしてその一方で、
![]()
は、2 つの交差した線の方向ベクトル間の外積の振幅です。
2 つの交差した線の間の距離を決定する方法を確認できるように、例として問題を解決します。
- 次に交差する 2 本の線の間の距離はいくらですか?
![]()
![]()
まず、方向ベクトルと各線上の点を特定する必要があります。したがって、2 つの直線は連続方程式の形式で表現されます。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8b990f78d0263975304586abbd330167_l3.png)
次に、交差する 2 つの線の間の距離の公式を適用します。
![]()
一方で、混合積 (または 3 倍のスカラー積) を解きます。
![]()
![Rendered by QuickLaTeX.com \left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13](https://mathority.org/wp-content/ql-cache/quicklatex.com-c52c12945d04e320e688caf714569113_l3.png)
一方、外積 (または外積) のモジュールを見つけます。
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}](https://mathority.org/wp-content/ql-cache/quicklatex.com-71afa7d4b49e542300c12b5263858665_l3.png)
![]()
最後に、2 つの交差した線の間の距離を表す式の各項の値を代入します。
![]()