平行面

7月 10, 2023

このページには、平行平面に関するすべてが表示されます。2 つの平面が平行である場合、2 つの平行平面の方程式、例、解決された演習、プロパティなどです。

2 つの平行な平面とは何ですか?

解析幾何学では、2 つの平面が常に同じ距離離れている場合、それらの平面は平行になります。したがって、2 つの平行な平面は決して交差せず、共通点はありません。

平行面の概念

空間 (R3) 内の 2 つの平面は交差したり一致したりする可能性があるため、平行に配置された 2 つの平面だけが平面間の相対位置として考えられるわけではありません。

2 つの平面が平行かどうかはどうやってわかりますか?

平行面の定義を理解した後、2 つの面が平行かどうかを判断する方法を見てみましょう。

2 つの異なる計画の一般 (または暗黙の) 方程式から開始します。

$\pi_1 : \ A_1x+B_1y+C_1z+D_1 =0$

$\pi_2 : \ A_2x+B_2y+C_2z+D_2 =0$

2 つの平面の係数 A、B、C が係数 D に比例せず、互いに比例する場合、2 つの平面は平行になります。つまり、2 つの平面間の平行度は、次の方程式が満たされるときに発生します。

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white ]}]{equation*} \cfrac{A_1}{A_2}=\cfrac{B_1}{B_2} = \cfrac{C_1}{C_2}\neq \cfrac{D_1}{D_2} \end{empheq}$

2 つの平行な平面の例

たとえば、次の 2 つの平面は平行です。

$\pi_1 : \ 6x+2y-4z+1 =0$

$\pi_2 : \ 3x+y-2z+5 =0$

変数 X、Y、Z の係数は互いに比例しますが、独立項には比例しないため、計画は並列です。

$\cfrac{6}{3} =\cfrac{2}{1} =\cfrac{-4}{-2} \neq \cfrac{1}{5} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

2 つの平行な平面間の距離を計算します

2 つの平行な平面は常に同じ距離離れているため、2 つの平行な平面間の距離を見つけるには、2 つの平面の一方の点を取得し、その点からもう一方の平面までの距離を計算できます。したがって、2 つの平行な平面間の距離を計算するには、点から平面までの距離の公式を知っている必要があります。

2 つの平行な平面間の距離

2つの平行な面の間の距離を求める方法です。ただし、2 つの平面の方程式の係数 A、B、C が一致する場合、これを行うさらに簡単な方法があります。

2 つの平行な平面の一般 (または暗黙的な) 方程式を考えてみましょう。

$\pi_1 : \ Ax+By+Cz+D_1=0 \qquad \qquad \pi_2 : \ Ax+By+Cz+D_2=0$

2 つの平行な平面間の距離を計算する式は次のとおりです。

$\color{orange} \boxed{\color{black} \quad d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}} \quad \vphantom{\Biggl(}}$

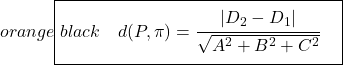
したがって、公式を使用して 2 つの平行な平面の間の距離を見つけるのは確かに簡単です。公式を適用するだけで済むためですが、それは問題によって異なります。さらに、距離を計算する両方の方法について説明し、好みの方法を選択できるようにすることが最善であると考えます。

2 つの平行な平面間の距離の計算例

例として、次の 2 つの平面間の距離を計算します。

$\pi_1 : \ 4x-2y-4z+7=0 \qquad \qquad \pi_2 : \ 8x-4y-8z+2=0$

まず、2 つの平行な平面を扱っていることを確認する必要があります。したがって、平面方程式のすべての係数は独立項を除いて比例するため、事実上 2 つの平行な平面になります。

$\cfrac{4}{8}=\cfrac{-2}{-4}=\cfrac{-4}{-8}\neq \cfrac{7}{2} \quad \longrightarrow \quad \pi_1 \parallel \pi_2$

この場合、2 つの平面の方程式の項 A、B、C は一致しませんが、2 番目の平面の方程式全体を 2 で割ることによってこれを実現できます。

$\pi_2 : \ \cfrac{8x-4y-8z+2}{2}=\cfrac{0}{2}$

$\pi_2 : \ 4x-2y-4z+1=0$

したがって、2 つの平面の方程式の係数 A、B、C は同じになります。したがって、2 つの平行な平面間の距離の公式を使用して、2 つの平面間の距離を簡単に計算できます。

$d(P,\pi) = \cfrac{\lvert D_2-D_1\rvert}{\sqrt{A^2+B^2+C^2}}$

値を代入して演算を解決します。

$d(P,\pi) = \cfrac{\lvert 1-7\rvert}{\sqrt{4^2+(-2)^2+(-4)^2}}= \cfrac{\lvert -6\rvert}{\sqrt{36}} = \cfrac{6}{6} = \bm{1}$

つまり、一方の平面ともう一方の平面の間の距離は 1 に等しくなります。

平行面の性質

平行面の特徴は次のとおりです。

反射特性: 各平面はそれ自体に平行です。

$\pi_1 \parallel \pi_1$

対称性: ある平面が別の平面に平行な場合、この平面も最初の平面と平行になります。この性質は垂直面にもあります。

$\pi_1 \parallel \pi_2 \ \longrightarrow \ \pi_2 \parallel \pi_1$

推移的プロパティ: ある平面が別の平面に平行で、この 2 番目の平面が 3 番目の平面に平行である場合、最初の平面も 3 番目の平面に平行になります。

$\left. \begin{array}{c} \pi_1 \parallel \pi_2\\[2ex] \pi_2 \parallel \pi_3 \end{array} \right\} \longrightarrow \ \pi_1 \parallel \pi_3$

コメントする返信をキャンセル