このページでは、楕円の離心率の意味とその計算方法(計算式)を説明します。さらに、楕円の離心率の計算例も表示されます。
楕円の離心率はいくらですか?
楕円の離心率は、楕円がどの程度丸いか平らであるかを測定するパラメータです。つまり、楕円の離心率は、楕円が円にどの程度似ているかを示します。
一方、楕円が何で構成されているかも思い出してください。楕円は、他の 2 つの固定点 (焦点 F および F’ と呼ばれます) までの距離の合計が一定である平面のすべての点の軌跡です。
楕円の離心の計算式
楕円の離心率の定義を理解したら、その式からどのように計算されるかを見てみましょう。
楕円の離心率の公式は次のとおりです。
![]()
金:
-

は楕円の離心率です
-

楕円の焦点 (点 F および F’) からその中心までの距離です。
-

は、楕円の長半径 (または長軸) の長さです。
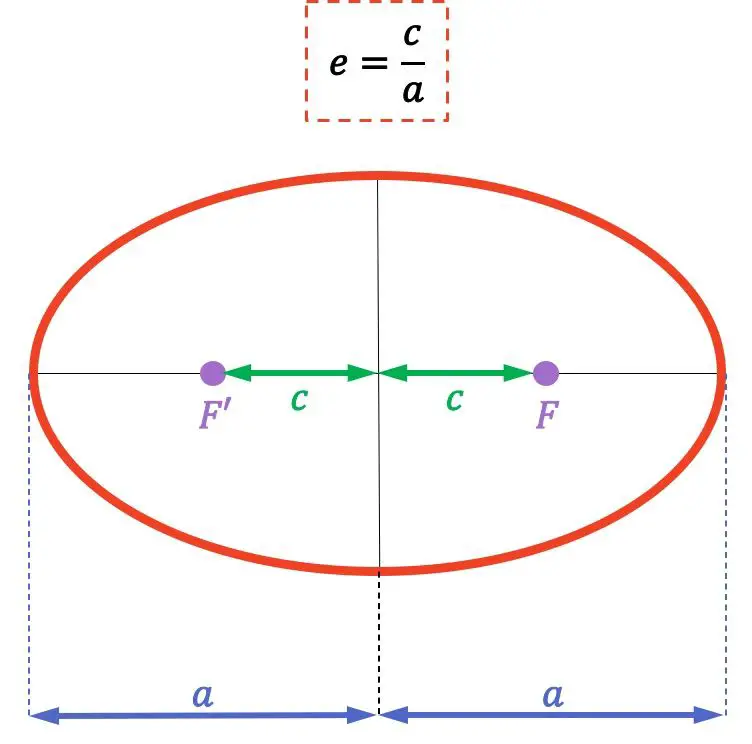
楕円の焦点は、楕円上の任意の点までの距離の合計が一定である固定点であることに注意してください。また、2 つの焦点間の距離は焦点距離と呼ばれます。
離心率の値の範囲は、完全な円であることを意味する 0 から、水平線であることを意味する 1 までです。結果として得られる幾何学的オブジェクトは楕円ではなくなるため、明らかに 0 と 1 は含まれません。

![]()
d(P,F)
![]()
d(P,F’)
![]()
もっている
![]()
もっている

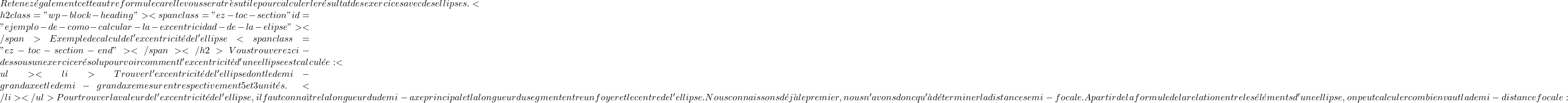
![]()
もっている
![]()
対、
![]()
e= \cfrac{c}{a} = \cfrac{4}{5} = \bm{0.8} $