不連続性の種類

9月 17, 2023

ここでは、どのような種類の不連続性が存在するかを確認します。さらに、あらゆる種類の不連続性の例を確認でき、関数の不連続性の種類に関する解答済みの演習を使用して練習することができます。

あらゆる種類の不連続性とは何ですか?

不連続性には次の 3 つのタイプがあります。

回避可能な不連続性: ある点における関数の横方向の限界が関数の値と一致しません。
避けられない有限ジャンプの不連続性: ある点における関数の横方向の限界が異なります。
避けられない無限ジャンプの不連続性: 関数の横方向の制限の 1 つが無限大を与えるか、存在しません。

概念の理解を終えるために、各タイプの不連続性をより詳細に説明し、3 つのタイプの不連続性を使用した関数の例を見ていきます。

回避可能な不連続性

回避可能な不連続性は、その点に境界が存在するが、関数の値と一致しない場合、または関数のイメージが存在しない場合に、その点に関数がある不連続性の一種です。

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a) \qquad | \qquad \displaystyle \exists\lim_{x \to a} f(x) \text{ y } \ \cancel{\exists} \ f(a)$

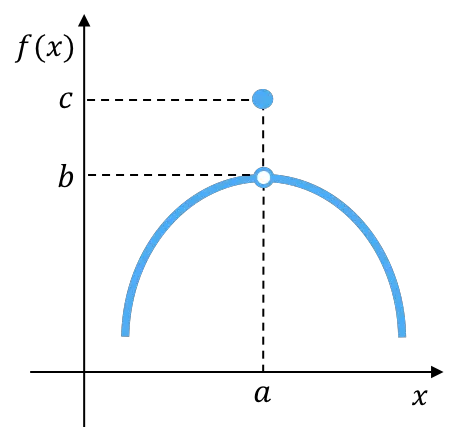
この関数の横方向の限界は互いに等しいですが、それらはその時点での関数の値とは異なります。したがって、関数は回避可能な不連続性を示します。

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad f(a)=c$

$\displaystyle \exists \lim_{x \to a} f(x) \neq f(a)$

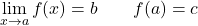
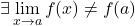
前の例の関数には、x=a での横方向の限界が同じ値を持つため、回避可能な不連続性がありますが、この点での関数のイメージは存在しません。

$\displaystyle \left. \begin{array}{l}\displaystyle \lim_{x \to a^-} f(x) =b \\[3ex] \displaystyle \lim_{x \to a^+} f(x)=b \end{array} \right\} \ \bm{\longrightarrow} \ \lim_{x \to a} f(x)=b$

$\displaystyle \lim_{x \to a} f(x)=b \qquad \cancel{\exists} \ f(a)$

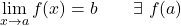
➤参照:関数の横方向の制限

有限ジャンプの必然的な不連続性

避けられない有限ジャンプの不連続性は、ある点での関数の横方向の限界が等しくないときに、その点で関数を表す不連続性の一種です。

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

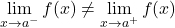
たとえば、定義変更点における次の区分的に定義された関数の横方向の限界は異なるため、関数にはその点で避けられない有限ジャンプの不連続性が生じます。

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=c$

$\displaystyle \lim_{x \to a^-} f(x) \neq \lim_{x \to a^+} f(x)$

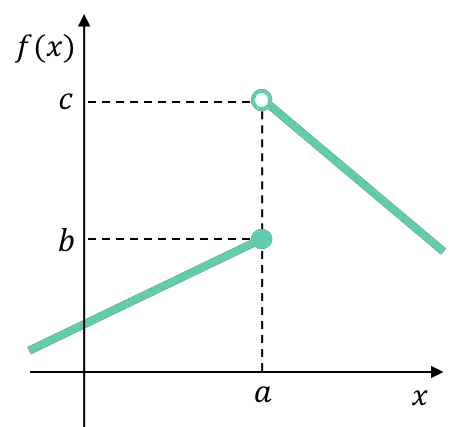
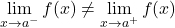
このタイプの不連続性は一般に、区分的に (または区分的に) 定義された関数に現れます。

➤参照:区分関数の連続性

無限ジャンプ必然の断絶

避けられない無限ジャンプの不連続性は、その点での横方向の制限の 1 つが無限であるか存在しない場合に機能する不連続性の一種です。

$\displaystyle \lim_{x \to a^-} f(x) = \pm \infty \qquad \lim_{x \to a^+} f(x)= \pm \infty$

次の関数の左限は実数を与えますが、右限は無限大を与えます。したがって、この関数には無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to a^-} f(x)=b \qquad \lim_{x \to a^+} f(x)=+\infty$

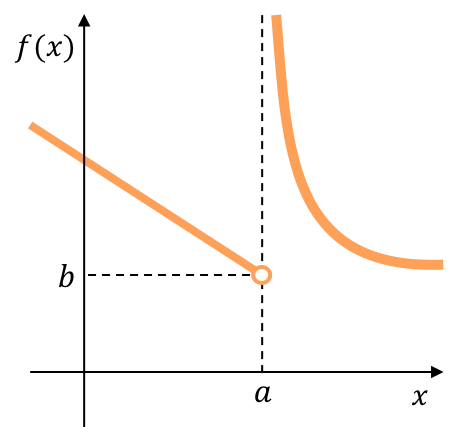
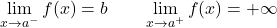
以下に、両側の限界が無限大を与えるグラフ関数を示します。したがって、この関数には無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to a^-} f(x)=-\infty \qquad \lim_{x \to a^+} f(x)=+\infty$

このタイプの不連続は通常、有理 (または分数) 関数で発生します。

不連続性の種類に関する解決された演習

演習 1

次の区分関数の点 x=3 における不連続性のタイプを決定します。

$\displaystyle f(x)= \left\{ \begin{array}{lcl} -2x+1 & \text{si} & x\leq 3 \\[2ex] 4x - 5 & \text{si} & x > 3 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”232″ style=”vertical-align: 0px;”></p> </p> <div class=$

解決策を見る

関数の最初の要素のドメイン、

$-2x+1$

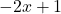
、2枚目と同じように、

$4x-5$

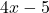
、多項式関数であるため、すべて実数です。

したがって、関数が不連続になる可能性がある唯一の点は、区分関数の停止点です。したがって、この段階で横方向の制限を計算します。

$\displaystyle \lim_{x \to 3^-} f(x)=\lim_{x \to 3} (-2x+1) = -2\cdot 3+1=-5$

$\displaystyle \lim_{x \to 3^+} f(x)=\lim_{x \to 3}(4x-5)=4\cdot 3-5=7$

$\displaystyle \lim_{x \to 3^-} f(x) \neq \lim_{x \to 3^+} f(x)$

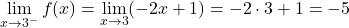
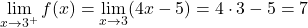
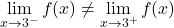
x=3 での 2 つの横方向の制限により、異なる結果が得られます。したがって、点 x=3 は避けられない有限ジャンプの不連続です。

演習 2

次の有理関数がその領域に属さない点でどのような種類の不連続性を示すかを調べます。

$f(x)= \cfrac{x^2-4}{x+2}$

解決策を見る

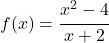
論理的には、この演習を解決するには、まず関数の定義域を見つける必要があります。したがって、これは有理関数であるため、分母を 0 に設定し、結果の方程式を解きます。

$x+2=0$

$x=-2$

$\text{Dom } f = \mathbb{R} - \{-2\}$

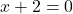
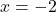
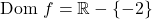
したがって、関数は x=-2 を除くすべての点で連続となるため、点 x=-2 がどのような種類の不連続であるかを見てみましょう。これを行うために、次の点での関数の限界を計算します。

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2} = \cfrac{ (-2)^2-4}{-2+2}= \cfrac{0}{0}$

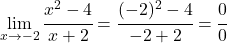
しかし、ゼロ間の不確定性はゼロになるため、分子と分母の多項式を因数分解して単純化します。

$\displaystyle \lim_{x \to -2} \cfrac{x^2-4}{x+2}=\lim_{x \to -2} \cfrac{ (x-2)\cancel{(x+2)}}{\cancel{x+2}} =\lim_{x \to -2} (x-2)$

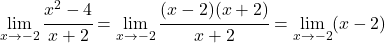
次に、制限を解決します。

$\displaystyle \lim_{x \to -2} (x-2) =-2-2=-4$

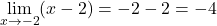
したがって、点 x=-2 における関数の極限は存在し、-4 を与えます。では、存在するかどうかを確認してみましょう

$f(-2):$

$f(-2)=\cfrac{(-2)^2-4}{-2+2}= \cfrac{4-4}{0} = \cfrac{0}{0} \quad \bm{\longrightarrow} \quad \cancel{\exists} \ f(2)$

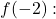
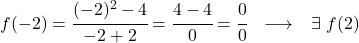
関数のイメージを計算する場合、不確定性 0/0 は単純化できず、解がありません。それで

$f(-2)$

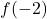
存在しない。

結論として、x=-2 における関数の極限は存在しますが、

$f(-2)$

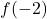
いいえ。したがって、x=-2 は回避可能な不連続点です。

演習 3

次の有理関数の連続性を分析します。

$\displaystyle f(x)= \frac{2}{x-5}$

解決策を見る

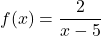
連続関数かどうかを確認するには、まずその定義域を計算する必要があります。したがって、どの点がドメインに属していないのかを確認するために、有理関数の分母をゼロに設定します。

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

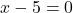
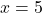
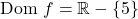
したがって、関数は x=5 を除くすべての点で連続になります。この時点での限界を計算して、x=5 がどのような種類の不連続性であるかを見てみましょう。

$\displaystyle \lim_{x \to 5} \frac{2}{x-5} = \frac{2}{5-5} = \frac{2}{0} = \infty$

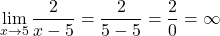
数値を 0 で割った値が不確定であることに気づきました。したがって、x=5 での関数の横方向の極限を計算します。

$\displaystyle \lim_{x \to 5^{-}} \frac{2}{x-5}=\frac{2}{4,999-5}=\frac{2}{-0}= \bm{-\infty}$

$\displaystyle \lim_{x \to 5^{+}} \frac{2}{x-5}=\frac{2}{5,001-5}=\frac{2}{+0}=\bm{+\infty}$

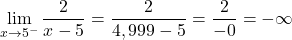
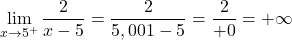
x=5 での関数の左の限界はマイナスの無限大を与え、右の限界はプラスの無限大を与えます。したがって、この点で少なくとも 1 つの横方向の限界が無限大になる傾向があるため、この関数には x = 5 で無限ジャンプの不連続性が避けられません。

演習 4

次のグラフに示されている区分関数の不連続点をすべて決定します。

解決策を見る

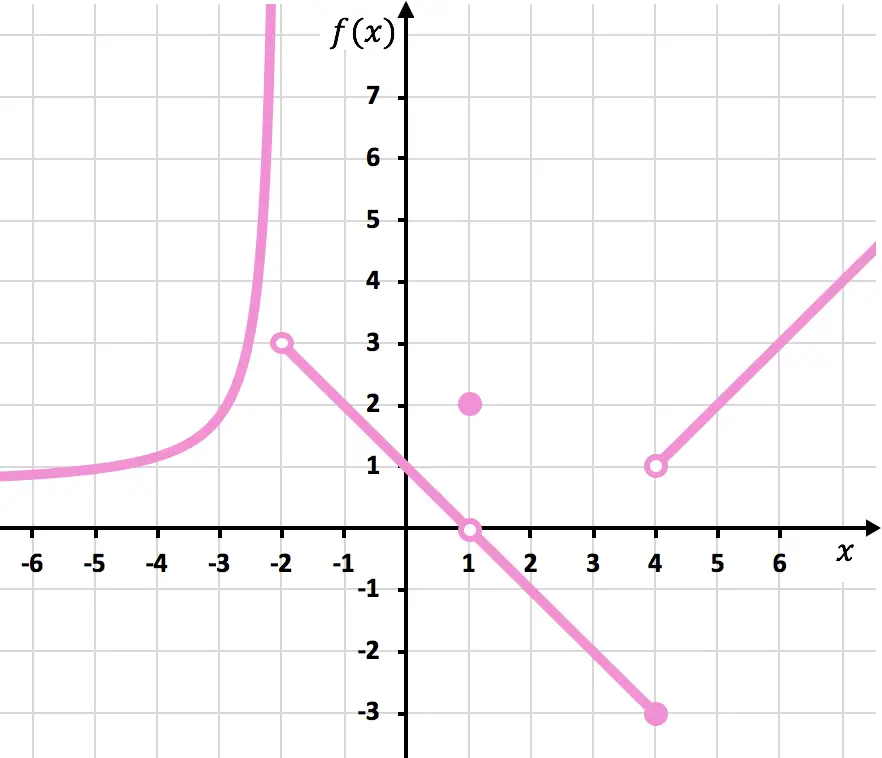
関数を描くには、x=-2、x=1、x=4 の位置で鉛筆を持ち上げる必要があります。したがって、関数はこれら 3 つの点で不連続になります。

x=-2 では、左側の限界は +∞ で、右側の限界は 3 です。したがって、側面の限界の 1 つが無限であるため、関数には x=-2 で無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

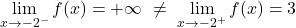
x=1 での関数の限界は 0 であり、一方、x=1 での関数の値は 2 に等しい。したがって、この関数は x=1 で回避可能な不連続性を示します。

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(1) = 2$

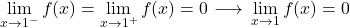
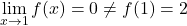
x = 4 では、左側の限界は -3 で、右側の限界は 1 です。したがって、2 つの辺の限界は異なり、どちらも無限大を与えないため、関数には必然的に x =4 で有限ジャンプの不連続性が生じます。

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

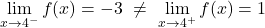
演習 5

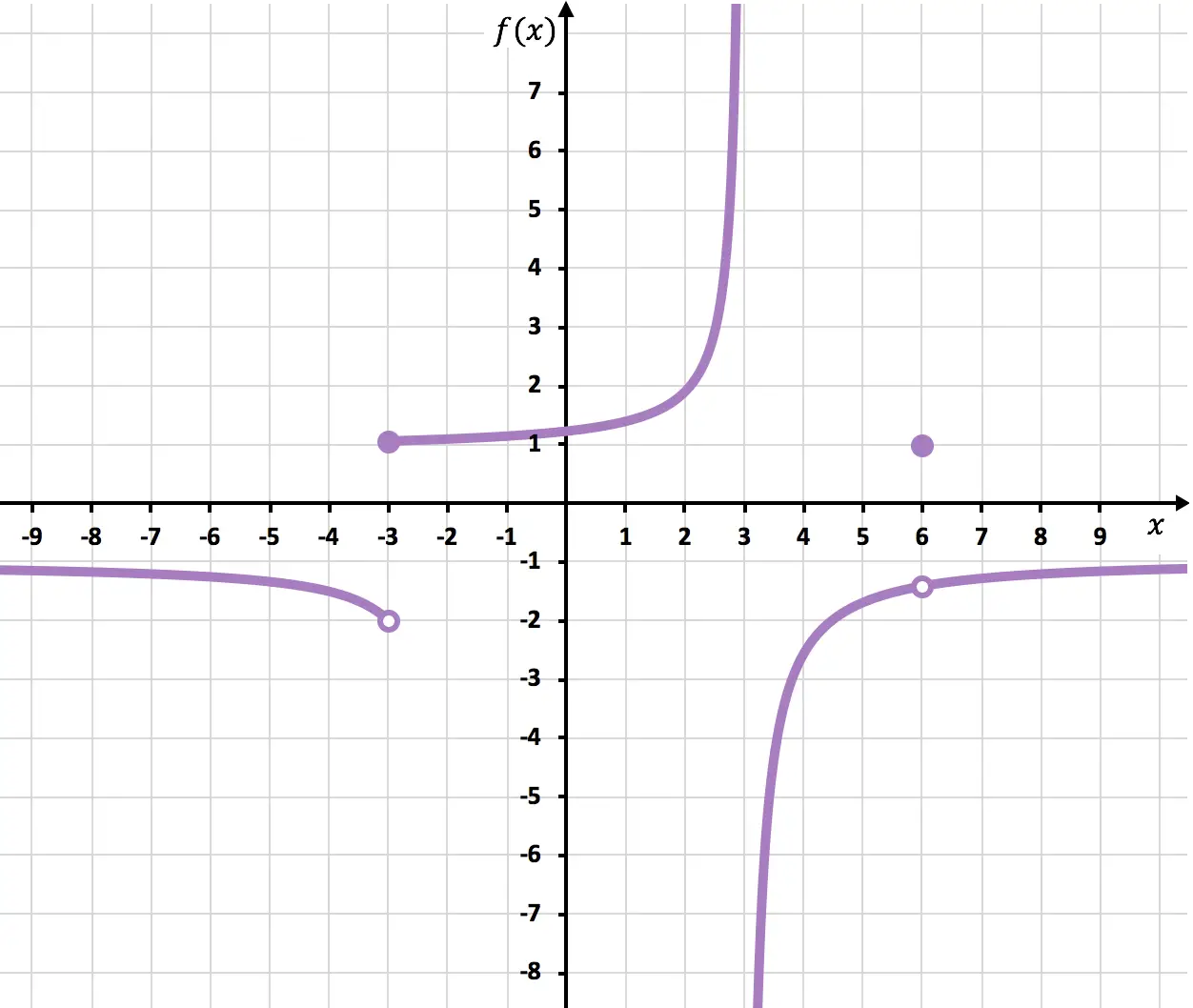
次のグラフで表される関数のすべての漸近線と不連続点を見つけます。

解決策を見る

漸近線

この関数は垂直線 x=3 に非常に近いですが、接触することはありません。さらに、x=3 での左側の横限界は +∞、右側の横限界は -∞ です。したがって、x=3 は垂直方向の漸近線になります。

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

そして、同じことが水平線 y=-1 でも起こり、関数は y=-1 に非常に近づきますが、それを横切ることはありません。さらに、x が +∞ および -∞ に近づくときの関数の限界は -1 です。したがって、y=-1 は水平方向の漸近線になります。

$\displaystyle \lim_{x \to +\infty} f(x)=-1 \qquad \lim_{x \to -\infty} f(x)=-1$

不連続性

x=6 では、開いた点があるため、関数は中断されます。 x が 6 に近づくときの限界は -1.4 ですが、f(6)=1 になります。したがって、制限の値が関数の値と一致しないため、関数には x=6 で回避可能な不連続性があります。

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

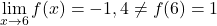
x=-3 では、横方向の限界は一致せず、どれも無限大を与えません。したがって、関数には x=-3 で有限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

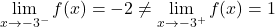
そして最後に、この時点で少なくとも 1 つの横方向の限界が無限大になるため、この関数には x = 3 で無限ジャンプの不連続性が避けられません。

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

あらゆる種類の不連続性とは何ですか?

回避可能な不連続性

有限ジャンプの必然的な不連続性

無限ジャンプ 必然の断絶

不連続性の種類に関する解決された演習

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

無限ジャンプ必然の断絶

コメントする返信をキャンセル