このページでは、ラインの点と傾きの方程式の公式と、それを計算するためのさまざまな方法がわかります。さらに、いくつかの例を見て、段階的に解決される演習で練習することができます。
直線の点と傾きの方程式の公式
直線の点と傾きの方程式は、直線を数学的に表現する方法です。特に、直線の点と傾きの方程式を求めるには、直線上の点の傾きと座標のみが必要です。
直線の点と傾きの方程式の式は次のとおりです。
![]()
金
![]()
は線の傾きであり、
![]()
線上の点の座標です
![]()
例を使用して、ラインの点と傾きの方程式がどのように計算されるかを見てみましょう。
- 点を通る直線の点と傾きの方程式を書きます。
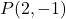
傾き m = 3。
直線の点と傾きの方程式の式は次のとおりです。
![]()
この場合、ステートメントは直線の傾きが m=3 であることを示しているため、直線の方程式は次のようになります。
![]()
さらに、線が点を通過することもわかります。
![]()
したがって、この点の座標を方程式に代入する必要があります。
![]()
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
点と傾き方程式以外にも、ベクトル方程式、パラメトリック方程式、連続方程式、陰的な方程式 (または一般)、陽的な線の方程式など、線を解析的に表現する方法があることに注意してください。さらに興味がある場合は、当社の Web サイトでそれぞれがどのようなものであるかを確認してください。
線の傾きは何を意味しますか?
直線の点と傾きの方程式の定義で見たように、パラメータは
![]()
線の傾きです。しかし実際には…線の傾きは何を意味するのでしょうか?これを線のグラフィック表現から見てみましょう。
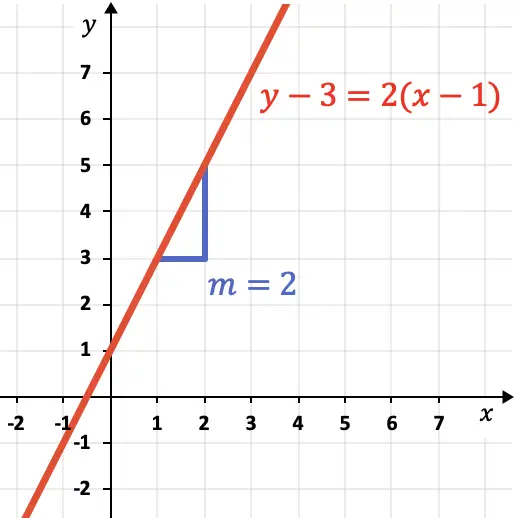
線の傾きはその急峻さを示します。グラフの線からわかるように、
![]()
ラインは 1 水平単位に対して 2 垂直単位ずつ上昇するため、 は 2 に等しくなります。
明らかに、傾きが正の場合、関数は増加 (上昇) し、一方、傾きが負の場合、関数は減少 (下降) します。
線の傾きを計算する方法
さらに、線の傾きを数値的に決定するには 3 つの異なる方法があります。
- 直線上の 2 つの異なる点が与えられると、

そして

線の傾きは次のようになります。
- うん

は線の方向ベクトルであり、その傾きは次のとおりです。
- うん

は横軸 (X 軸) と線によって形成される角度であり、線の傾きはその角度の正接に相当します。
![]()
![]()
![]()

線の相対位置
最後に、線の傾きは、複数の線の間の関係を知るためにも使用されます。 2 本の平行な線は同じ傾きを持ち、一方の線の傾きが別の線の傾きの負の逆数である場合、これはこれら 2 本の線が垂直であることを意味します。


2 点を通る直線の点と傾きの方程式を計算します。
非常に一般的な問題は、直線に属する 2 つの点から点と傾きの方程式を決定することです。例を通してそれがどのように解決されるかを見てみましょう。
- 次の 2 点を通過する直線の点と傾きの方程式を求めます。
![]()
線の点と傾きの方程式を見つけるには、線の傾きを決定する必要があります。したがって、コロンの式を使用して線の傾きを計算します。
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
![]()
したがって、直線上の点のデカルト座標を方程式に代入するだけで済みます。
![]()
![]()
![]()
ステートメントの他の点を直線の方程式に入れるのも良いでしょう:
![]()
![]()
グラフから直線の点と傾きの方程式を求める
上のセクションで見たように、線の点と傾きの方程式を数値的に求める方法はいくつかあります。ただし、グラフで見つけることもできます。例を通してこれがどのように行われるかを見てみましょう。
- 次のグラフに示す直線の点と傾きの方程式を求めます。
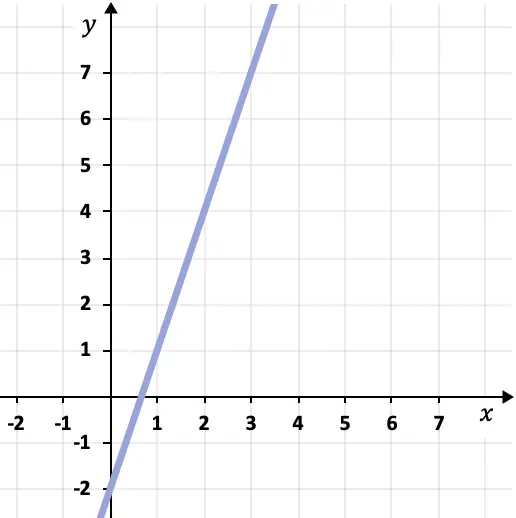
描かれた線の点と傾きの方程式を決定するには、その傾きと線上の点を見つける必要があります。
この場合、線は水平単位ごとに 3 垂直単位上がるため、線の傾きは 3 に等しくなります。
![]()
次に、線上に点が必要です。これを行うには、線が通過するグラフ上の任意の点、たとえば点 (1,1) を選択します。
![]()
したがって、次の式を適用して、線の点と傾きの方程式を見つけることができます。
![]()
![]()
点と傾きの方程式の問題を解決しました
演習 1
点を通る直線の点と傾きの方程式を書きます。
![]()
そしてその傾きは
![]()
直線の点と傾きの方程式の式は次のとおりです。
![]()
この場合、ステートメントは直線の傾きが m=-2 であることを示しているため、直線の方程式は次のようになります。
![]()
さらに、このステートメントから、線が点を通過することもわかります。
![]()
したがって、点の座標を直線の方程式に代入するだけで十分です。
![]()
![]()
演習 2
次の 2 点を通る直線の点と傾きの方程式は何ですか?
![]()
線の点と傾きの方程式を見つけるには、線の傾きを決定する必要があります。したがって、次の式を使用して線の傾きを計算します。
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
![]()
したがって、直線上の点の座標を方程式に代入するだけで済みます。
![]()
![]()
ステートメントのもう 1 つの点を方程式に入れるのも正しいはずです。
![]()
演習 3
次の 2 点を通過する直線の点と傾きの方程式を求めます。
![]()
直線の点と傾きの方程式を見つけるには、まずその傾きを計算する必要があります。
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
![]()
したがって、直線上の点の座標を方程式に代入するだけで済みます。
![]()
![]()
![]()
ステートメント内の他の点を直線の方程式に入れることも正しいです。
![]()
演習 4
X 軸と 45 度の角度を形成し、座標原点を通過する直線の点と傾きの方程式を計算します。
線が OX 軸に対して 45 度の角度をなす場合、その傾きは次のようになります。
![]()
![]()
![]()
直線の傾きがわかれば、直線上の点を方程式に代入することで点と傾きの方程式を見つけることができます。さらに、このステートメントは、線が座標原点を通過すること、つまり点 (0,0) を通過することを示しています。まだ:
![]()
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
演習 5
直線に平行な直線の点の傾きの方程式を求めます。
![]()
そしてその点で何が起こるか
![]()
まっすぐであること
![]()
![]()
線の傾き
![]()
は 2 (かっこの前の数字) に等しく、2 本の線が平行であるためには、それらの傾きが同じでなければなりません。したがって、次のようになります。
![]()
![]()
線の傾きがわかったら、その線に属する点の座標を式に代入するだけです。
![]()
![]()
したがって、直線の点と傾きの方程式は次のようになります。
![]()
演習 6
次のグラフに示されている各線の点と傾きの方程式を決定します。

青右
青い線は X ごとに Y が 1 ずつ増加するため、その傾きは 1 に等しくなります。一方、この線は点 (2,4) を通過するため、次のようになります。
![]()
右の緑
緑の線は X ごとに Y が 3 ずつ増加するため、その傾きは 3 になります。さらに、その点の 1 つは (2,2) であるため、次のようになります。
![]()
レッドライン
赤い線は X ごとに Y が 2 ずつ減少するため、その傾きは -2 になります。そして、点 (0,-2) はこの直線に属します。したがって、次のようになります。
![]()