この記事では、関数の斜め漸近線とは何かについて説明します。関数に斜めの漸近線がある場合と、それがどのように計算されるかを学びます。さらに、斜めの漸近線の例を確認し、段階的に解く演習で練習することもできます。
斜線漸近線とは何ですか?
関数の斜線漸近線は、グラフが決して交差することなく無限に近づく傾斜線です。したがって、すべての斜線の漸近線は、方程式y=mx+nの直線になります。
斜めの漸近線の傾きと原点は、次の式を使用して計算されます。
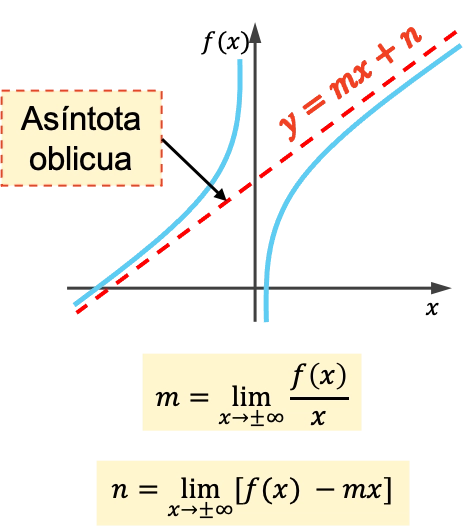
関数の斜線漸近線を計算する方法
関数の斜線漸近線を計算するには、次の手順を実行する必要があります。
- 関数の無限大の極限を x で割った値を計算します。
- 上記の制限の結果がゼロ以外の実数になる場合は、関数に斜めの漸近線があることを意味します。さらに、前記斜め漸近線の傾きは極限で得られる値となる。
- この場合、残っているのは、次の制限を解いて斜線の漸近線の切片を計算することだけです。
![]()
![]()
注:制限はプラス無限大とマイナス無限大で計算する必要がありますが、通常は同じ結果が得られるため、±∞ を置くことで簡略化します。ただし、プラス無限大とマイナス無限大での限界が異なる場合は、左斜めの漸近線と右斜めの漸近線を別々に計算する必要があります。
斜線漸近線の例
次に、次の有理関数の斜線漸近線を取得して、これがどのように行われるかの例を確認します。
![]()
斜めの漸近線は次のタイプです。
![]()
そこで、まず直線の傾きを計算します。
![]()
対応する式は次のようになります。
![]()
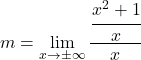
この制限を解決するには、分数のプロパティを適用する必要があります。
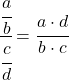
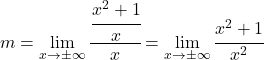
そして今、限界を計算します:
![]()
この場合、分子と分母が同じ次数であるため、無限大間の無限大の不確定性の結果は、最高次数の x の係数の除算になります。
上記の制限はゼロ以外の実数を与えるため、関数は斜めの漸近線を持ちます。ここで y 切片を計算します
![]()
対応する式を使用して漸近線を計算します。
![]()
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-1x\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-9197669cc0e41aa22224b552b21b31ed_l3.png)
制限を計算してみます。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4d7fa012eace37e82c243012c91f1a5c_l3.png)
しかし、無限から無限を引いた不確定性が得られます。したがって、項を共通の分母に減らす必要があります。これを行うには、x を分数の分母で乗算および除算します。
![Rendered by QuickLaTeX.com \displaystyle n=\lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x\cdot x}{x} \right] = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x}\right]](https://mathority.org/wp-content/ql-cache/quicklatex.com-a2355ed9411470b9fd20a50ebbd48726_l3.png)
2 つの項の分母が同じになったので、それらをグループ化できます。
![Rendered by QuickLaTeX.com \displaystyle n = \lim_{x \to \pm\infty} \left[\cfrac{x^2+1}{x}-\cfrac{x^2}{x} \right] = \lim_{x \to \pm\infty} \cfrac{x^2+1-x^2}{x}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f932ebc8728669c7c6b57e115c444fc7_l3.png)
分子を操作します。
![]()
そして最後に、制限を解決します。
![]()
したがって、 n = 0 となります。したがって、斜めの漸近線は一次関数になります。
![]()
![]()
![]()
研究した関数は以下のグラフに表されます。ご覧のとおり、この関数は線 y=x に非常に近づきますが、斜めの漸近線であるため、線に触れることはありません。

斜めの漸近線に関する解決された演習
演習 1
次の有理関数の斜めの漸近線を求めます。
![]()
斜めの漸近線は次の形式になります。
![]()
したがって、パラメーターmとnを計算する必要があります。まず、次の式を適用してmを計算します。
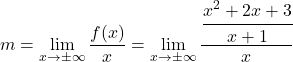
分数の性質を適用して分数を単純化します。
![]()
![]()
そして、その限界を解決します。
![]()
したがって、 m = 1 となります。ここで、公式を適用して斜めの漸近線の切片を計算してみましょう。
![]()
制限を計算してみます。
![]()
しかし、無限形式から無限大を引いた不定形式が得られます。したがって、項を共通の分母に減らしてからグループ化する必要があります。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-x\right] =\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x \cdot (x+1)}{x+1} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{x^2+2x+3}{x+1}-\frac{x^2+x}{x+1} \right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \frac{x^2+2x+3-(x^2+x)}{x+1}\\[6ex]\displaystyle =\lim_{x \to \pm\infty} \frac{x^2+2x+3-x^2-x}{x+1}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{x+3}{x+1}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0712d34ed442d9e12ef2490f04df078a_l3.png)
そして最後に、制限を解決します。
![]()
つまり、関数の斜線漸近線は次のようになります。
![]()
![]()
![]()
演習 2
次の有理関数のすべての斜線漸近線を見つけます。
![]()
まず、斜め漸近線の傾きの公式を使用します。
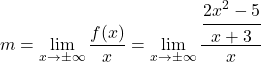
分数の性質を適用して分数を単純化します。
![]()
![]()
そして限界を決定します。
![]()
この極限はゼロ以外の実数を与えるため、傾きが 2 である斜めの漸近線を持つ有理関数になります。
次に、対応する式を適用して切片を計算しましょう。
![]()
制限を計算してみます。
![]()
しかし、無限大の差分不確定性が得られます。したがって、項を共通の分母に減らして、次の操作を行います。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle n = \lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-2x\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[\frac{2x^2-5}{x+3}-\frac{2x\cdot (x+3)}{x+3} \right] = \\[6ex]=\displaystyle\lim_{x \to \pm\infty} \left[ \frac{2x^2-5}{x+3}-\frac{2x^2+6x}{x+3}\right]=\\[6ex]=\displaystyle\lim_{x \to \pm\infty}\frac{2x^2-5-(2x^2+6x)}{x+3}\\[6ex]\displaystyle =\lim_{x \to \pm\infty}\frac{2x^2-5-2x^2-6x}{x+3}=\\[6ex]=\displaystyle \lim_{x \to \pm\infty} \frac{-6x-5}{x+3}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4920e8b21b180c4f2740ce712d9f30d0_l3.png)
そして最後に、制限を解決します。
![]()
要約すると、分数関数の斜線漸近線は次のようになります。
![]()
![]()