このページでは、右手の法則 (または法則) とは何か、およびそれがどのように使用されるかについて説明します。また、存在するルールの 3 つのバリエーションに加えて、ルールの例と実際の応用も確認できます。
右手の法則とは何ですか?
右手の法則または法則は、コルク栓抜きの法則としても知られ、ベクトルの方向とセンスを決定するために使用される手法です。つまり、右手の法則により、計算をしなくてもベクトルの方向と方向を知ることができます。主に、直線運動と回転運動の 2 種類の運動の方向を見つけるために使用されます。
以下は、右手の法則の 3 つのバリエーション(3 本の指を使う、手のひらを使う、コルク抜きの法則) の説明です。 3 つのルールは異なりますが、目的は同じであるため、そのうちの 1 つを適用する方法を知っておくだけで済みます。 3 つの説明の後、右手の法則の応用がわかります。
3本指の右手定規
右手の法則の最初のバージョンは 3 本の指で実行され、 2 つのベクトルのベクトル積の方向と方向を見つけるために使用されます。したがって、ルールは次のステップで構成されます。
- 右手の人差し指を外積の最初のベクトルの方向に置きます。

- 右手の中指(または中指)を外積の 2 番目のベクトルの方向に置きます。

- 結果として得られる親指の位置は、外積の方向と方向を示します。

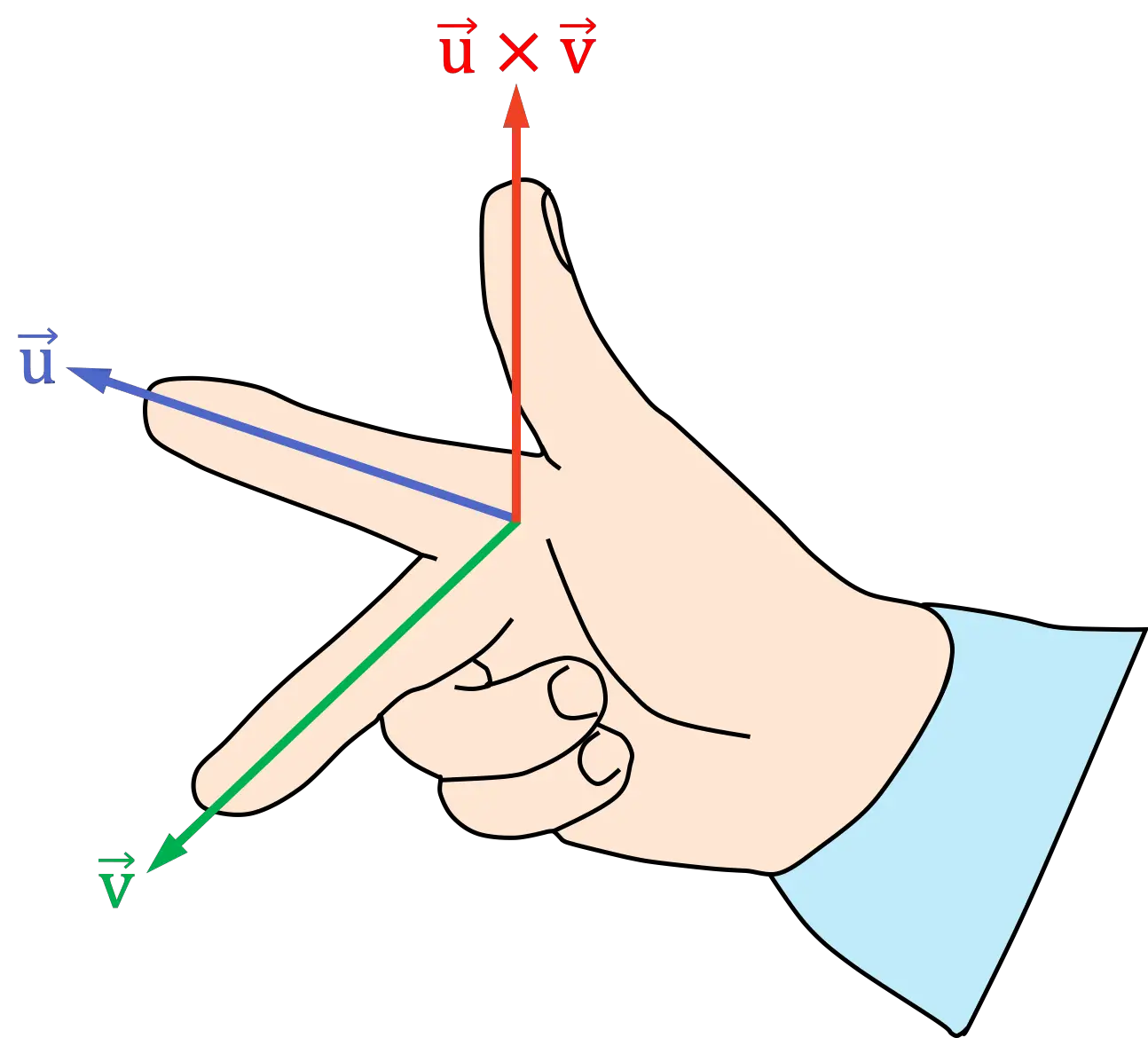
右手は手のひら全体で支配する
右手の法則または法則の 2 番目のバージョンは、手のひら全体で使用され、2 つのベクトル間の外積の方向と方向を決定するためにも使用されます。実際、これは前のバリアントと似ています。これを適用するには、次の手順に従う必要があります。
- 右手の人差し指を外積の最初のベクトルと同じ方向に置きます。

- 外積の 2 番目のベクトルに向かって指を動かして右手を閉じます。

ベクトル間の角度 (または距離) が最も小さい側で手を閉じる必要があります。
- 結果として生じる親指の位置によって、外積の方向が決まります。

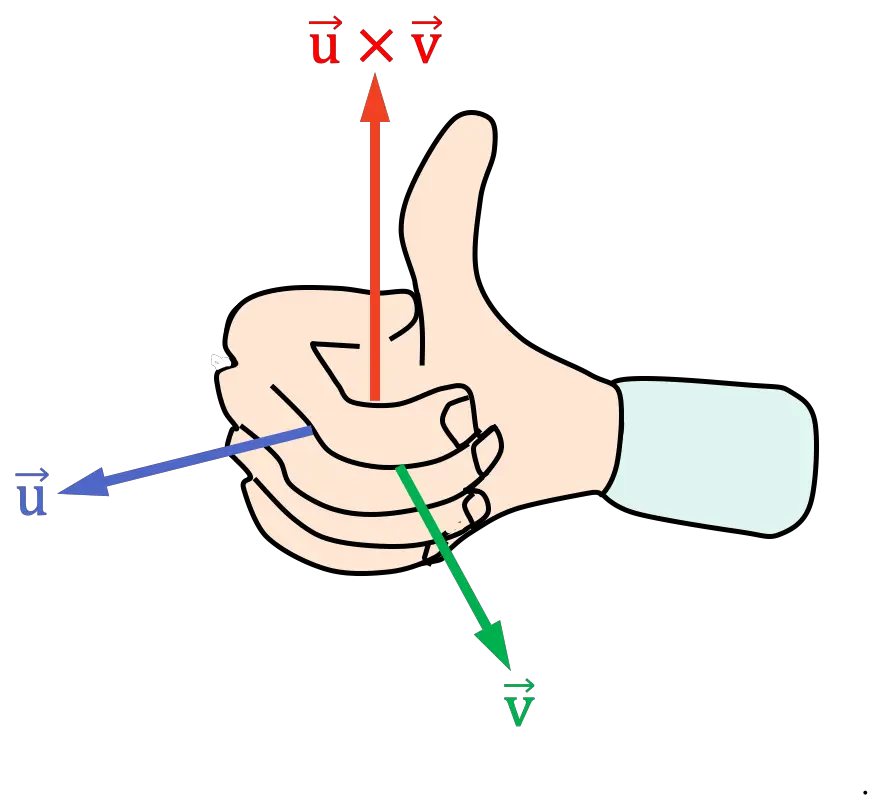
コルク抜きルール
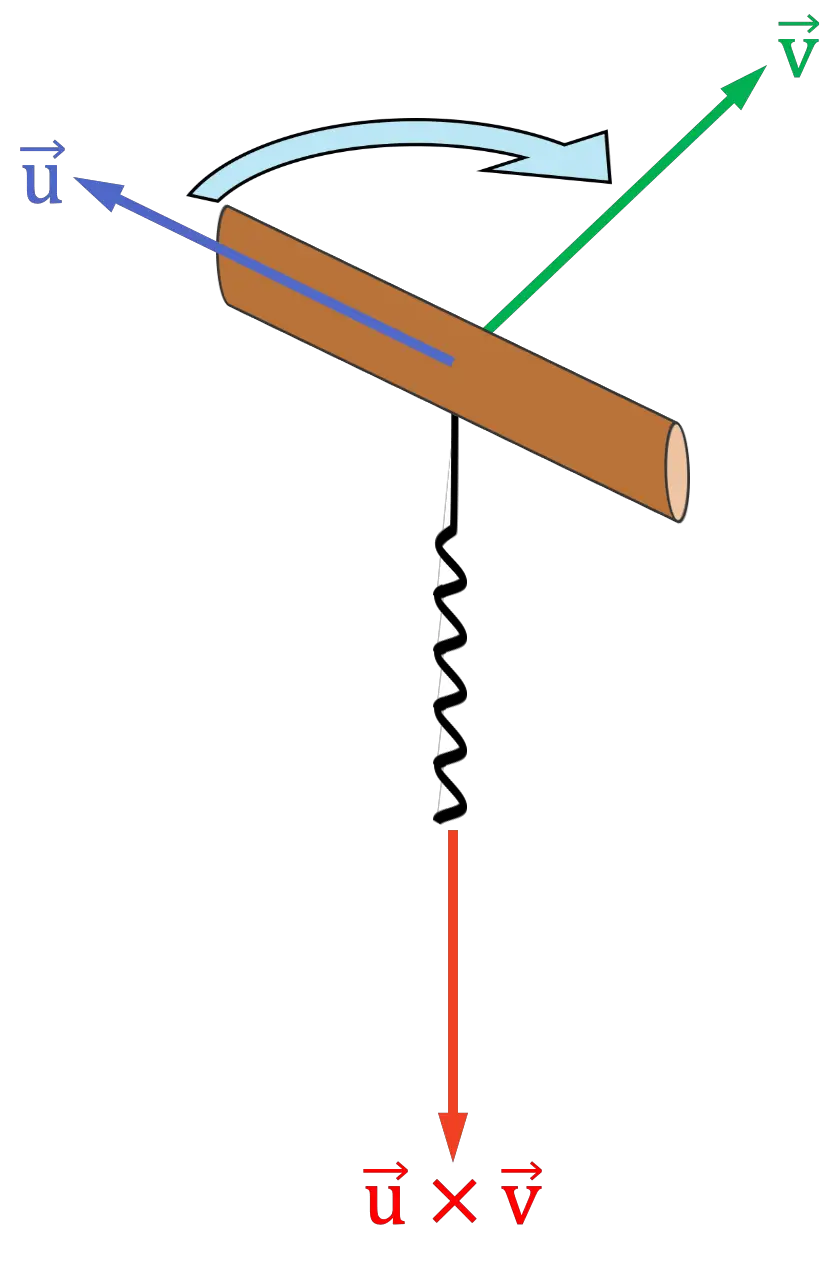
コルク栓抜きまたはねじの法則は、 2 つのベクトル間のベクトル積の方向と方向を知るためにも使用されます。その手順は次のとおりです。
- 想像力を働かせて、ハンドルが外積の最初のベクトルと同じ方向を向くようにコルク栓抜き (またはネジ) を配置します。

- 次に、コルク抜きを外積の 2 番目のベクトルに向けて回転させます。
まるでコルクに詰めるかのように。ベクトル間のパスが狭くなる側にコルク抜きを回す必要があります。
- コルク栓抜きの螺旋が指す方向がベクトル積の方向と方向になります。

右手の法則は何のためにあるのでしょうか?
右手の法則は、数学と物理学の両方で多くの実世界に応用されています。以下に最も重要なものを示します。
磁場
磁気学では、磁力の式には外積があるため、磁場が荷電粒子に及ぼす力の方向を計算するために右手の法則が使用されます。これはいわゆるローレンツの法則です。
![]()
金
![]()
は磁力、
![]()
粒子の電荷、
![]()
その速度のベクトルと
![]()
磁場のベクトル。
電磁場
電磁気学では、導体(ケーブル)に直流または交流が一定の強さで流れるとケーブルの周囲に電磁場が発生するため、右手の法則も使われます。したがって、この電磁場の方向は右手の法則を使用して見つけることができます。
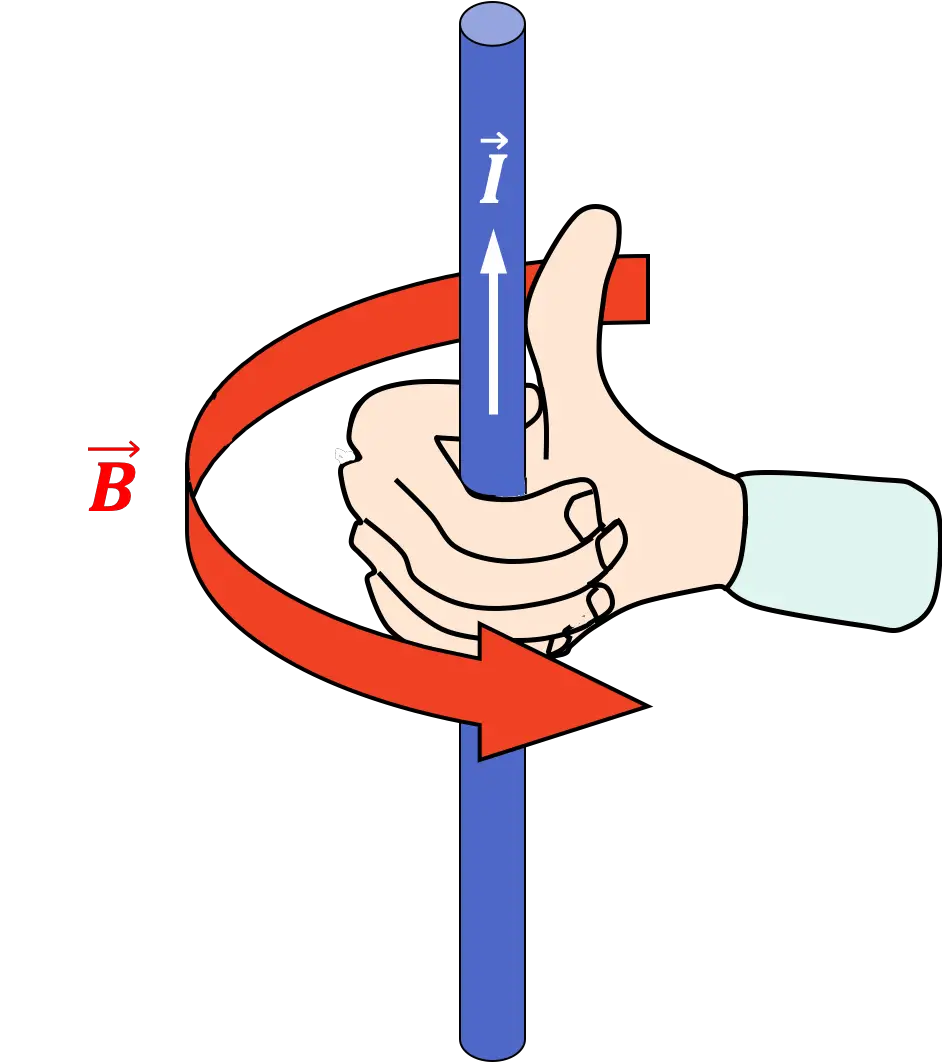
力の瞬間
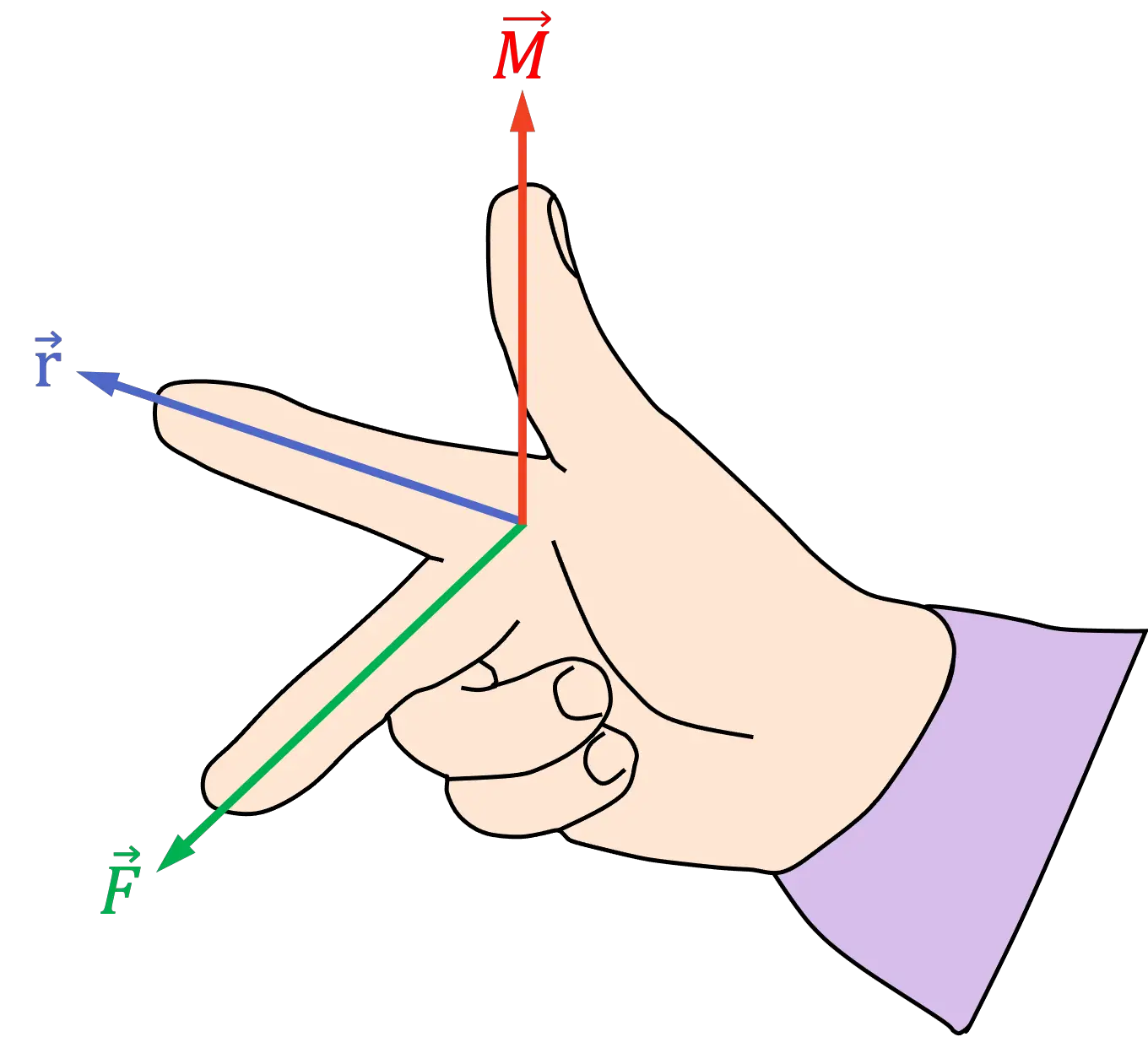
力の運動量の感覚は物理学、特に力学において非常に重要です。そして、モーメント方程式にはベクトル積が含まれるため、この意味は右手の法則を使用して簡単に取得できます。
![]()
金
![]()
力を加えた結果生じるモーメントです
![]()
そして
![]()
力の作用点と発生モーメントが計算される点の間の距離です。
角速度
右手の法則のもう 1 つの応用は、角速度ベクトルの方向を決定することです。このベクトルの意味を知るには、手のひら全体で適切なバージョンの定規を使用する必要があります。
次の図からわかるように、物体が時計回りに回転すると角速度ベクトルは入り(負)、反時計回りに回転すると角速度ベクトルは出ます(正)。

XYZ軸
最後に、右手の法則は、任意の 3 次元参照系を示すために使用することもできます。なぜなら、右手の法則に介入する3本の指(3本の指)を見ると、それらは互いに垂直であるため、X、Y、Z軸の方向としても機能するからです。