ベクトルの成分とは何か、またその計算方法は

このページでは、ベクトルの成分 (または座標) が何であるかについて説明します。また、2 つの点からどのように計算されるか、モジュールと角度を通じてどのように分解されるかも確認できます。さらに、ステップバイステップで解決される例と演習が表示されます。

ベクトルの成分は何ですか?

ベクトルのコンポーネントは、ベクトルをデカルト軸に投影したものです。したがって、ベクトルの x 軸への投影はベクトルの X 成分であり、同様に、ベクトルの y 軸への投影はベクトルの Y 成分です。

ベクトルの成分は、ベクトルの座標とも呼ばれます。

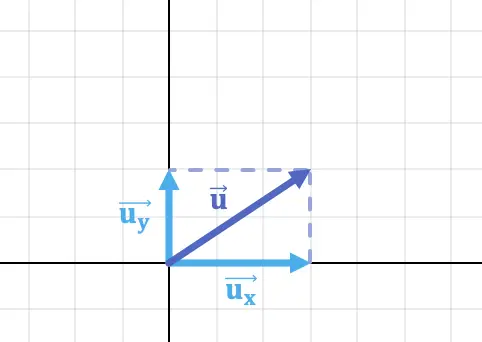
たとえば、上の画像のベクトルの水平成分と垂直成分は次のとおりです。

したがって、ベクトルは次のようになります。

したがって、ベクトルの成分は、座標系におけるベクトルの表現として定義することもできます。明らかに、それが 2 次元系 (r2 の場合) の場合、ベクトルは 2 つの成分を持ちますが、一方、3 次元の基底系 (r3 の場合) の場合、ベクトルは 3 つの成分で構成されます。

ベクトルのデカルト成分は、主にベクトルの方向、方向、係数 (または大きさ) などのベクトルの特性を知ることができるため、非常に重要です。さらに、ベクトル演算を実行するためにも使用されます。

2 点からベクトルの成分を計算する方法

ベクトルの座標をグラフィックで見つける方法を説明しましたが、その成分を数値的に決定することもできます。

ベクトルの成分を数値的に計算するには、ベクトルの始点と終点、つまりベクトルの始まりと終わりの 2 つの点を知る必要があります。ベクトルの成分は、その終点から原点を引いた座標であるため。

たとえば、原点が点 A(3,1) で終点が点 B(5,4) であるベクトルを計算します。

ご覧のとおり、ベクトルの成分を決定することはそれほど難しいことではありませんが、非常に重要です。たとえば、最も一般的に使用されるベクトルのタイプの 1 つは垂直 (または直交) ベクトルです。ベクトルの座標が何であるかを理解していれば、垂直ベクトルを計算するのは非常に簡単です。それがどのように行われるかは、直交ベクトルの説明で確認できます。

係数と角度からベクトルの成分を計算する方法

ベクトルの大きさと X 軸との角度からベクトルの成分を見つけることもできます。このプロセスはベクトル分解と呼ばれます。

したがって、ベクトルの X 成分と Y 成分は、コサインとサインの三角比を使用して計算できます。

画像からわかるように、ベクトルの係数とその成分は直角三角形を完成させるため、三角法の基本公式を適用できます。

ベクトルの係数の計算方法を覚えていない場合は、 ベクトルの係数を調べることができます。ここでは、ベクトルの大きさの公式、例、ステップバイステップで解決される演習、およびベクトルの大きさのすべての特性を見つけることができます。非常に丁寧な説明なので、完璧に理解できるでしょう。 ✅

常に正であるベクトルの大きさとは異なり、サインとコサインは負の値をとる可能性があるため、その成分は負になる可能性があります。

例として、モジュールと OX 軸との角度が次のようなベクトルのベクトル分解を実行します。

ベクトルの X 成分は、モジュールに角度のコサインを乗算したものに等しくなります。

そして、ベクトルの Y 成分はモジュールと角度の正弦の積に等しくなります。

したがって、ベクトルの座標は次のようになります。