ベクトルの係数を計算する方法

このページでは、ベクトルの大きさの説明と、その公式を使用してベクトルを計算する方法を説明します。また、モジュールの起点と終点の 2 つのポイントからモジュールを見つける方法もわかります。さらに、ベクトルの係数とベクトルの係数のプロパティからベクトルの成分を決定する方法を学びます。例、演習、段階的な問題で練習することもできます。

ベクトルの係数とは何ですか?

ベクトルの大きさは、その始点と終点の間の距離を表します。したがって、ベクトルの大きさは、そのベクトルの長さに等しい。

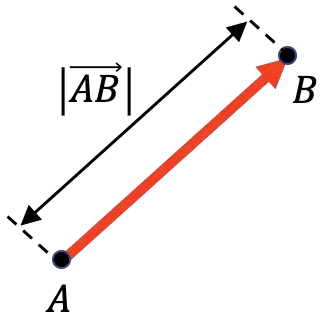
上の図でわかるように、ベクトルの大きさは、ベクトルの両側の垂直バーで表されます。

$\lvert \vv{AB}\rvert$

一方、ベクトルの係数はベクトルのノルムと同じなので、そのように書かれていることもわかります。これが、各辺に 2 本の垂直バーを持つベクトルのモジュールを表す数学者がいる理由です。

$\lvert \lvert \vv{AB}\rvert\rvert$

ベクトルの係数の公式

平面内のベクトルの大きさを求めるには、次の公式を適用する必要があります。

ベクトルの大きさを決定するには、その成分の二乗和の (正の) 平方根を計算する必要があります。言い換えると、次のベクトルがあるとします。

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

そのモジュールは次のとおりです。

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

たとえば、次の式を使用して次のベクトルの大きさを計算します。

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

始点と終点の座標を使用してベクトルの大きさを計算します。

ベクトルの成分がわかっているときにベクトルの大きさがどのように決定されるかを見てきましたが、ベクトルの開始点と終了点だけがわかっている場合はどうなるでしょうか?

したがって、ベクトルの始点と終点の座標からベクトルの大きさを計算するには、次の 2 つの手順に従う必要があります。

まず、ベクトルの成分を見つけます。これを行うには、極値から原点を引く必要があります。
そして、前のセクションで見た式で得られたベクトルのモジュールを計算します。

例を通してこれがどのように行われるかを見てみましょう。

点を原点とするベクトルの大きさを計算します
$A(2,1)$

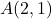
そして最後のポイントとして

$B(-1,4).$

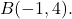
まずベクトルの成分を見つける必要があるので、その終点から原点を引いた値を引きます。

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

ベクトルがわかったら、ベクトルの大きさの公式を使用してその大きさを計算します。

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

結果は正確ではないため、平方根のままにします。

係数からベクトルの成分を計算する方法

ベクトルの成分からベクトルの大きさを抽出する方法を説明しましたが、このプロセスを逆にすることもできます。言い換えれば、係数を通じてベクトルの成分を計算できます。

ベクトルの大きさからベクトルの成分を見つけるプロセスは、ベクトル分解と呼ばれます。したがって、ベクトルを分解するには、明らかにその大きさと、横軸 (X 軸) との角度が必要です。

ベクトルの X 成分と Y 成分を三角比で計算できるようにするには、次のようにします。

画像からわかるように、ベクトルの大きさはその成分とともに直角三角形を形成するため、三角法の基本公式を適用できます。

ベクトルの法とは異なり、サインとコサインは負の値をとる可能性があるため、その成分は負になる可能性があることを考慮する必要があります。

例として、OX 軸との大きさと角度が次のようなベクトルのベクトル分解を解きます。

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

ベクトルの水平成分は、モジュールに角度のコサインを乗算したものに等しくなります。

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

そして、ベクトルの垂直成分は、モジュールに角度の正弦を乗算したものと等しくなります。

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

したがって、ベクトルは次のようになります。

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

ベクトルの係数プロパティ

モジュラスは、次の特性を持つベクトル演算の一種です。

ベクトルの大きさは負になることはなく、常に 0 以上になります。

$\lvert \vv{\text{u}} \rvert \geq 0$

実際、大きさがゼロで存在する唯一のベクトルはゼロベクトル、つまりベクトルです。

$\vv{\text{u}}= (0,0) .$

ベクトルと実数 (またはスカラー) の積の大きさは、スカラーの絶対値にベクトルの大きさを乗算することと同じです。したがって、次の等式が成り立ちます。

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

三角不等式が検証されます。2 つのベクトルの和の係数は、それぞれのベクトルのモジュールの合計以下になります。

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

さらに、2 つのベクトルの合計の大きさは、次の方程式によってドット積に関連付けられます。

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

単位ベクトル

数学では、単位ベクトルとは、その法が 1 に等しいベクトルです。

$\lvert \vv{\text{u}} \rvert=1$

したがって、単位ベクトルの長さは 1 単位になります。

ベクトルの法が正確に 1 であることは非常に難しいように思えるかもしれませんが、このタイプのベクトルを見つけるのは実際には簡単です。

任意のベクトルの単位ベクトルを見つけるには、単純にその係数で割ります。

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

金

$\vv{\text{v}}_u$

はの単位ベクトルです

$\vv{\text{v}},$

そして

$\lvert \vv{\text{v}} \rvert$

あなたのモジュール。

単位ベクトルは、バーサーまたは正規化ベクトルとも呼ばれます。

さらに、単位ベクトルは元のベクトルと同じ方向と方向を持ちます。

たとえば、次のベクトルの単位ベクトルを計算します。

$\vv{\text{v}}=(1,-1)$

ベクトルを正規化するには、まずその大きさを計算する必要があります。

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

そして最後に、元のベクトルをその係数で除算して単位ベクトルを計算します。

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

ベクトルモジュールの演習を解決しました

演習 1

次のベクトルの大きさを計算します。

$\vv{a}=(6,8)$

解決策を参照

ベクトルのモジュールを計算するには、その式を適用する必要があります。

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

演習 2

次のベクトルを最短から最長の順に並べます。

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

解決策を参照

ベクトルの長さはその大きさに等しい。したがって、すべてのベクトルの係数を計算する必要があります。

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

したがって、長さ (またはモジュール) を最小のものから最大のものまで並べたベクトルは次のようになります。

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

演習 3

点を原点とするベクトルの大きさを求める

$A(-3,2)$

そして最後のポイントとして

$B(7,-4).$

解決策を参照

モジュールを計算するには、まずベクトルを見つける必要があります。これを行うには、極値から原点を差し引きます。

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

ベクトルがわかったら、その係数は係数の公式を使用して計算されます。

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

演習 4

次のベクトルを分解し、そのコンポーネントを見つけます。

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

解決策を参照

ベクトルの水平成分は、モジュールに角度のコサインを乗算したものに等しくなります。

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

そして、ベクトルの垂直成分は、モジュールに角度の正弦を乗算したものと等しくなります。

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

したがって、ベクトルは次のようになります。

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

この場合、2 つの成分は同一です。つまり、ベクトルの傾斜角は 45 度です。

演習 5

次のベクトルと同じ方向と方向で、ただしモジュール 1 を使用してベクトルを計算します。

$\vv{a} = (-4,3)$

解決策を参照

モジュール 1 と同じ方向のベクトルが単位ベクトルです。それを計算するには、まずベクトルのモジュールを見つけます。

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

そして、元のベクトルをその係数で割って単位ベクトルを計算します。

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

演習 6

次のベクトルをベクトル分解し、その単位ベクトルを計算します。

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

解決策を参照

まず、ベクトルを分解し、その座標を見つけます。

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

したがって、ベクトルは次のようになります。

$\vv{a}= (5,64 \ ,\ 2,05)}$

そして、モジュールによって取得されたベクトルを除算して単位ベクトルを計算します。

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

単位ベクトルの成分は、X 軸となす角度のコサインとサインに等しいことに注意してください。

ベクトルの係数とは何ですか?

ベクトルの係数の公式

始点と終点の座標を使用してベクトルの大きさを計算します。

係数からベクトルの成分を計算する方法

ベクトルの係数プロパティ

単位ベクトル

ベクトルモジュールの演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

コメントする 返信をキャンセル

コメントする返信をキャンセル