ベクトル減算 - マソリティ

このページでは、2 つのベクトルを減算する方法をグラフィックと数値の両方で説明します。それらをグラフィカルに減算するには、平行四辺形、三角形、多角形の 3 つの方法があります。ここでは、各方法の長所と短所を区別できます。さらに、例、演習、問題を段階的に解決することができます。

2 つのベクトルをグラフィカルに減算するにはどうすればよいですか?

ベクトルを幾何学的に減算する方法はいくつかあります。もちろん、すべての方法で同じ結果が得られますが、お好みの方法を選択できるように、すべての方法を説明します。 👌

2 つのベクトルのみを減算するには、平行四辺形法と三角形法という2 つのグラフィカルな手順があります。ただし、3 つ以上のベクトルの減算を解決したい場合は、ポリゴン法を使用する必要があります。

それでは、これ以上苦労することなく、これらすべてのメソッドについて以下に説明します。

平行四辺形の方法または規則

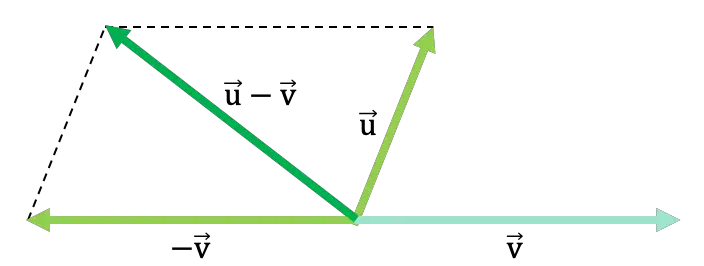
平行四辺形の法則または平行四辺形法は、非常に簡単な方法でグラフィック表現を通じて 2 つのベクトルの減算を求めることができる手順です。このプロセスを適用するために実行する手順は次のとおりです。

まず、グラフ上で 2 つのベクトルを表し、それらを同じ適用点に配置します。つまり、両方のベクトルの原点を同じ点に配置します。
次に、演算で減算されるベクトルの逆のベクトルを描画します。つまり、減算されるベクトルを反転します。
次に、追加されたベクトルの末尾に、符号が変更されたベクトルに平行な線を描きます。そして、他のベクトルでも同じプロセスを繰り返します。これにより、平行四辺形の描画が行われます (これがルールの名前の由来です)。
最後に、減算の結果は、2 つのベクトルの共通原点から 2 つの平行線が交差する点までのベクトルになります。

平行四辺形法を使用して 2 つのベクトルを減算する、次の一般的な例を考えてみましょう。

三角形のメソッドまたはルール

三角形法は、2 つのベクトルをグラフから減算できる別の手順です。この場合、従うべき手順は次のとおりです。

2 つのベクトルを同じ適用点に配置します。つまり、2 つのベクトルの原点が同じ点になるようにします。
ベクトル減算の結果は、減算するベクトルの終わりからもう一方のベクトルの終わりまでのセグメントです。よく見ると、2つのベクトルが減算され、もう1つのベクトルが減算されて三角形が完成します。

以下は、三角形法を使用したベクトル減算の例です。

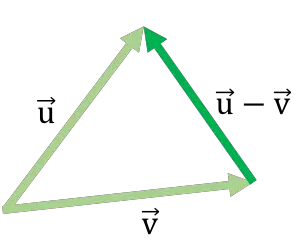
ベクトルを減算するこの方法は、ベクトルを追加するために使用される先頭と末尾の方法に似ています。

ポリゴン法

2 つのベクトルの減算をグラフィカルに解決する方法を確認したら、3 つ以上のベクトルがある場合にそれがどのように行われるかを見ていきます。

3 つ以上のベクトルを減算する場合、計算を高速化してすべてのベクトルを一度に減算する手法があります。この手法はポリゴン法と呼ばれ、ベクトル加算の先頭から末尾までの手法を連続的に適用することで構成されます。

おそらく、ベクトルを追加することを考えているでしょう。間違って修正されてしまいました…いやいや！え、え、

2 つのベクトルを減算することは、ベクトルと、減算するベクトルの反対側 (または負の) ベクトルを加算することと同じであることがわかります。これは、ベクトルの加算および減算の特性によるものです。

$\vv{a} - \vv{b} =\vv{a} +(-\vv{b})$

したがって、ポリゴン法で 3 つ以上のベクトルを減算するには、次の手順に従う必要があります。

まず、各減算ベクトルの逆ベクトルを見つける必要があります。減算されるすべてのベクトルの方向と方向を反転するのと同じくらい簡単です。
次に、減算しないベクトルの隣に、反対のベクトルを順番に配置します。ベクトルの始点が別のベクトルの終点と一致するようにします。
最後に、ベクトル減算の結果は、最初のベクトルの始まりと最後のベクトルの終わりを結合することによって得られるベクトルです。

4 つのベクトルで減算が行われる次の例を見てください。

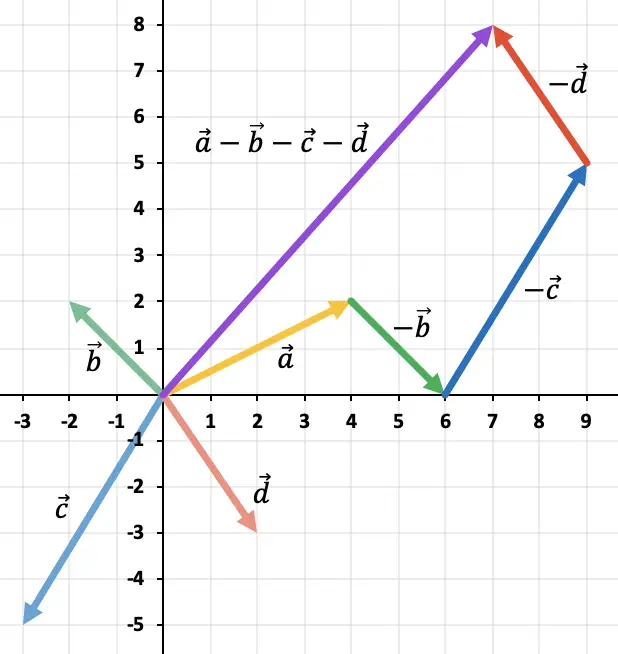
ベクトルの反対のベクトルを見つけるには、そのベクトルの 2 つの成分の符号が変わる必要があることに注意してください。

2 つのベクトルの減算を数値的に計算するにはどうすればよいですか?

グラフからベクトルを減算する方法がわかったら、数値的または代数的にベクトルの減算を計算する方法を見ていきます。

2 つのベクトルを数値的に減算するには、それぞれの成分を減算する必要があります。言い換えると、2 つのベクトルの X 座標が相互に減算され、同様に Y 座標とも減算されます。

$\vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)$

$\vv{\text{u}} - \vv{\text{v}} = (\text{u}_x - \text{v}_x \ , \ \text{u}_y - \text{v}_y)$

たとえば、ベクトル間の減算

$\vv{\text{u}} = (4,1)$

そして

$\vv{\text{v}}=(2, 3)$

東：

$\vv{\text{u}} = (4,1) \qquad \vv{\text{v}}=(2, 3)$

$\begin{aligned} \vv{\text{u}} - \vv{\text{v}}& =(4,1) -(2, 3) \\[2ex] & = (4-2,1-3) \\[2ex] & = \bm{(2,-2)} \end{aligned}$

ベクトル減算の問題を解決しました

演習 1

ベクトル減算をグラフィカルに計算する

$\vv{a}$

少ない

$\vv{b}:$

解決策を参照

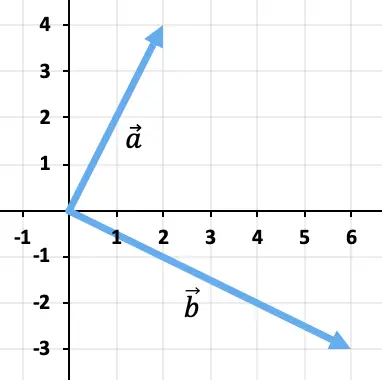
2 つのベクトルを減算するには、三角法を使用します。点はすでに同じ適用点 (座標の原点) に配置されているため、減算の結果は、座標の終端からのベクトルになります。

$\vv{b}$

の終わりに

$\vv{a}.$

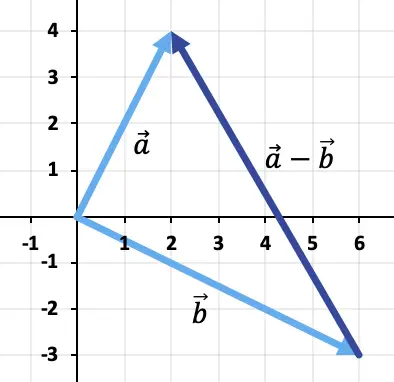
演習 2

ベクトルの減算をグラフィカルに求める

$\vv{a}$

少ない

$\vv{b}:$

解決策を参照

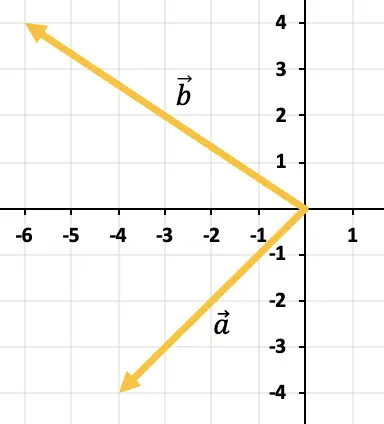
2 つのベクトルを減算するには、三角定規を使用します。点はすでに同じ適用点 (X 軸と Y 軸の始点) に配置されているため、減算の結果は終点からのベクトルになります。

$\vv{b}$

の終わりに

$\vv{a}.$

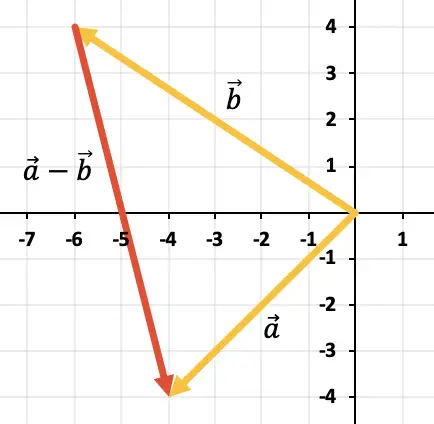
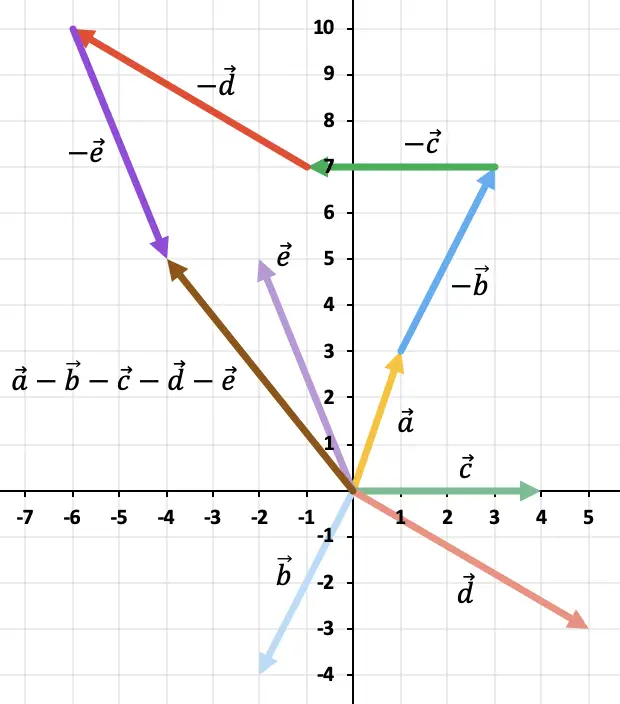
演習 3

次のベクトル演算をグラフィカルに解きます。

$\vv{a}-\vv{b}-\vv{c}-\vv{d}-\vv{e}$

解決策を参照

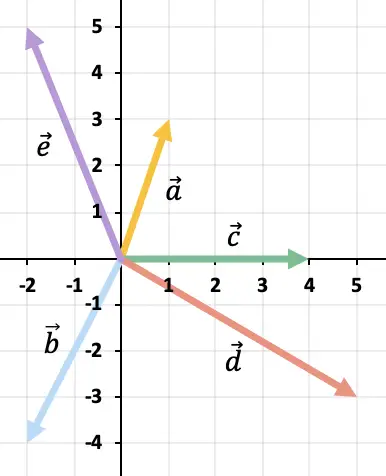
ベクトルが 2 つ以上あるため、ポリゴンルールを使用してベクトルの減算を解決します。これを行うには、残りのベクトルの反対のベクトルを次々に表す必要があります。そして結果はベクトルの原点から始まるベクトルになります

$\vv{a}$

最後の反対ベクトルが終了する場所まで。

演習 4

次のベクトルを減算した結果を数値的に求めます。

$\vv{a}=(-1,5) \qquad \vv{b}=(3,-2)$

$\vv{a}-\vv{b}$

解決策を参照

2 つのベクトルを数値的に減算するには、それぞれの座標を減算する必要があります。

$\begin{aligned} \vv{a}-\vv{b}& =(-1,5)-(3,-2) \\[2ex] & = (-1-3 ,5-(-2))\\[2ex] & = (-4 ,5+2)\\[2ex] & =\bm{(-4,7)} \end{aligned}$

演習 5

次のベクトル演算を解析的に解きます。

$\vv{a}=(2,4) \qquad \vv{b}=(-1,4)\qquad \vv{c}=(0,2)\qquad \vv{d}=(3,-7)$

$\vv{a}-\vv{b} -\vv{c}-\vv{d}$

解決策を参照

ベクトルを数値的に (または分析的に) 減算するには、それぞれの成分を減算する必要があります。

$\begin{aligned} \vv{a}-\vv{b}-\vv{d}-\vv{d}& =(2,4)-(-1,4)-(0,2)-(3,-7) \\[2ex] & =(3,0)-(0,2)-(3,-7) \\[2ex] & =(3,-2)-(3,-7) \\[2ex]& =\bm{(0,5)} \end{aligned}$

2 つのベクトルをグラフィカルに減算するにはどうすればよいですか?

平行四辺形の方法または規則

三角形のメソッドまたはルール

ポリゴン法

2 つのベクトルの減算を数値的に計算するにはどうすればよいですか?

ベクトル減算の問題を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル