ベクトルの追加

このページでは、平面内で 2 つのベクトルを加算する方法をグラフィックと数値で説明します。それらをグラフィカルに追加するには、平行四辺形、頭から尾まで、および多角形の方法の 3 つの方法があります。さらに、ベクトル加算とベクトル加算のすべてのプロパティに関する解決済み演習も見つかります。

2 つのベクトルをグラフィカルに追加するにはどうすればよいですか?

基本的に、グラフ表現からベクトルを追加するには 2 つの方法があります。どちらの形状でも同じ結果が得られますが、頭尾法を使用してそれらを追加することを好む人もいれば、平行四辺形法を使用することを好む人もいます。したがって、お好みの方法を選択できるように、2 つの方法について説明します。 😉

一方、これら 2 つの方法は 2 つのベクトルを追加するために使用されますが、3 つ以上のベクトルを追加したい場合はどうなるでしょうか?したがって、平行四辺形法を連続して使用する多角形法を使用する必要があります。頭尾法と平行四辺形法の後にもその説明があります。

平行四辺形の方法または規則

平行四辺形の法則または平行四辺形法(または平行四辺形の法則) は、非常に簡単な方法で 2 つのベクトルの和を求めることができるグラフィカルな手順です。このプロセスを適用するために実行する手順は次のとおりです。

1. まず、ベクトルを描画し、同じ適用点に配置します。つまり、両方のベクトルの原点を同じ点に配置します。
2. 次に、一方のベクトルの端に、もう一方のベクトルに平行な線を描きます。そして、他のベクトルでも同じステップを繰り返します。したがって、平行四辺形の描画が得られます (これがルールの名前の由来です)。
3. 最後に、合計の結果は、共通の原点から 2 本の平行線が交差する点まで向かうベクトルになります。

次の一般的な例を見てください。この例では、2 つのベクトルが平行四辺形の規則で追加されています。

ベクトルの合計の結果は、ベクトルが平行線で形成する平行四辺形の対角線になります。

ヘッドアンドテール方式

ヘッド アンド テール メソッド(またはトライアングル メソッド)は、2 つのベクトルをグラフィカルに追加できるもう 1 つの手順です。この場合、従うべき手順は次のとおりです。

1. 追加したベクトルを移動し、その原点がもう一方の追加したベクトルの端に来るように配置します。
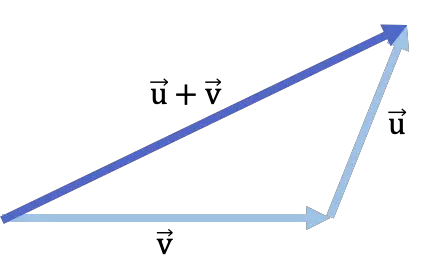
2. ベクトル加算の結果は、最初に追加されたベクトルの先頭からもう一方のベクトルの末尾までのセグメントになります。よく見ると、2つのベクトルを足し、さらにベクトルを足して三角形が完成します。

以下は、head-to-tail 法を使用したベクトル加算の例です。

ポリゴン法

2 つのベクトルの合計をグラフィカルに解く方法を確認したら、3 つ以上のベクトルがある場合にそれがどのように行われるかを見ていきます。

3 つ以上のベクトルを加算する場合、演算の計算を高速化する手法があります。この手法はポリゴン法と呼ばれ、頭から尾まで法を連続的に適用することで構成されます。

1. まず、あるベクトルの始点が別のベクトルの終点と一致するように、各ベクトルを他のベクトルの後に配置する必要があります。それらを配置する順序は重要ではありません。
2. そして、合計の結果は、最初のベクトルの始まりと最後のベクトルの終わりを結合することによって得られるベクトルです。

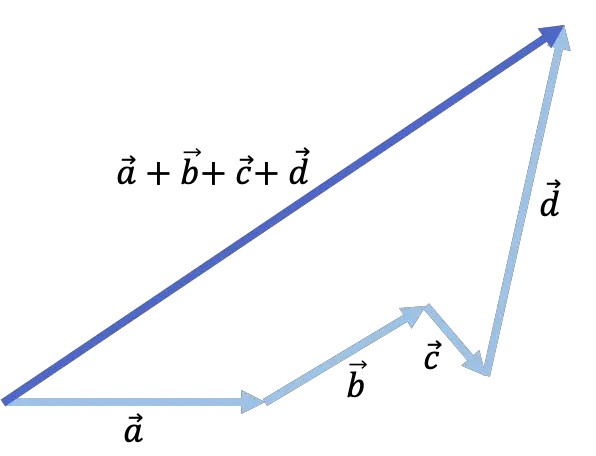
4 つのベクトルが追加される次の例を見てください。

2 つのベクトルの合計を数値的に計算します。

ベクトルを幾何学的に加算する方法がわかれば、数値的または代数的にベクトルの合計を計算する方法がわかります。

たとえば、ベクトル間の和

そして

東：

一方、2 つのベクトルのベクトル加算は、ベクトルのモジュールの加算と同じではなく、実際、結果はまったく異なることに留意する必要があります。 2 つの演算の違いは、 ベクトルの大きさ(ベクトルの大きさとも呼ばれます) のプロパティで確認できます。

ベクトルプロパティの追加

ベクトル加算には次の特徴があります。

• 結合プロパティ: 複数のベクトルの合計の間に括弧を入れても、演算の結果は変更されません。

• 可換性の性質– ベクトルの減算とは異なり、2 つのベクトル間の加算の結果は、加算される順序には依存しません。

• 反対側の要素のプロパティ: ベクトルとその反対側、つまりその否定の合計は 0 に等しくなります。

• 中立要素のプロパティ: 明らかに、任意のベクトルに null または null ベクトルを加えたものは、ベクトル自体と同等です。

ベクトル加算の問題を解決しました

演習 1

ベクトルの合計をグラフィカルに計算する

そして

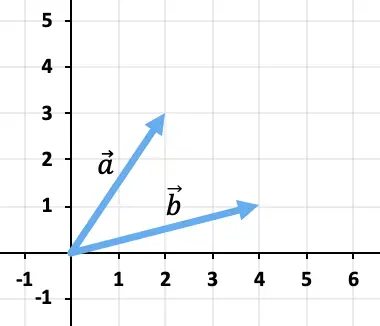
2 つのベクトルを加算するには、先頭と末尾の規則を使用します。したがって、ベクトルの原点を配置します。

ベクトルの最後に

、合計は座標の原点から座標の終わりまでのベクトルになります。

したがって、ベクトル加算の結果は次のようになります。

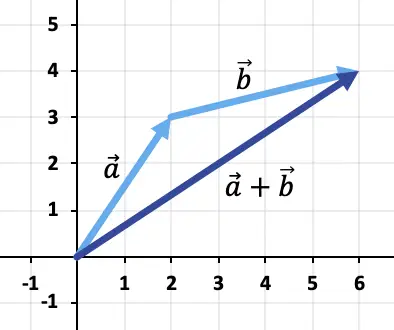
演習 2

ベクトルの和をグラフィカルに解く

そして

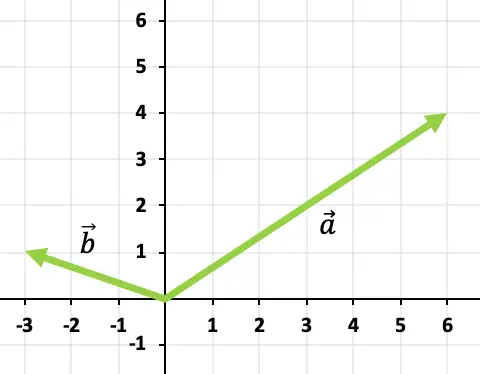
2 つのベクトルを加算するには、head-tail ルールを使用します。したがって、ベクトルの原点を特定します。

ベクトルの最後に

、合計ベクトルは軸の原点から軸の終端までのベクトルになります。

したがって、ベクトル加算の結果は次のようになります。

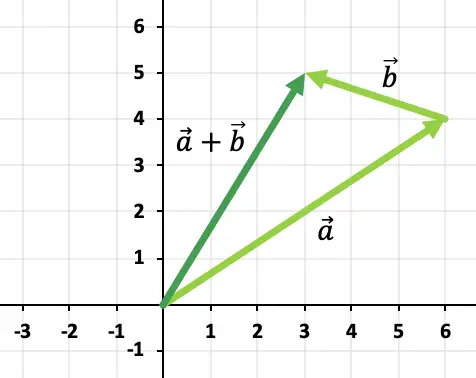
演習 3

グラフに表されているすべてのベクトルを加算した結果のベクトルをグラフィカルに決定します。

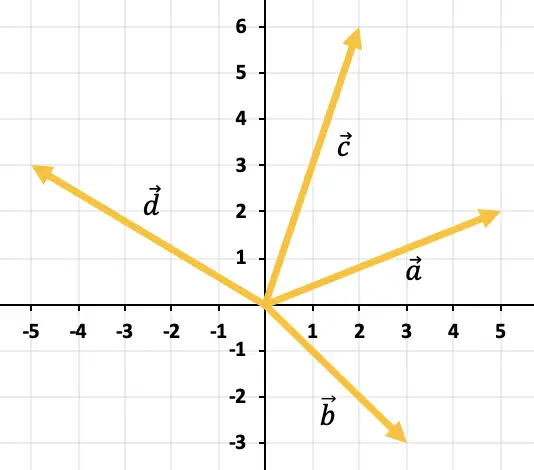
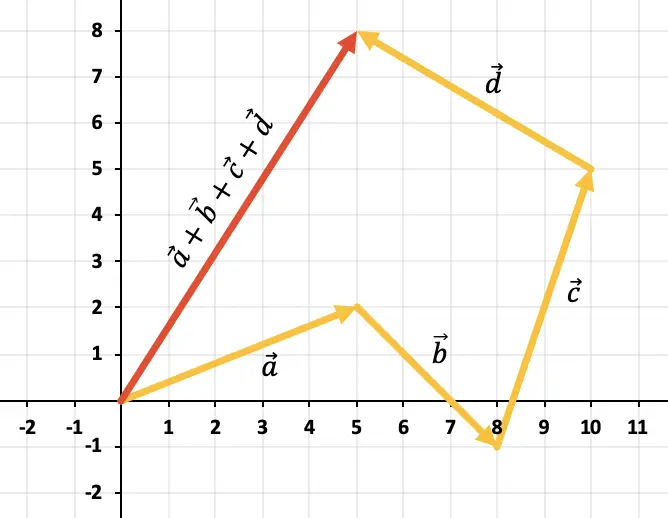
グラフから 3 つ以上のベクトルを追加するには、ポリゴン ルールを使用する必要があります。したがって、ベクトルが連続したままになるように、つまり次々にベクトルを移動する必要があります (順序は無関係です)。したがって、すべてのベクトルの合計は、最初のベクトルの原点から最後のベクトルの終わりまでのベクトルになります。

したがって、4 つのベクトルの合計の結果は、赤色で表されるベクトルになります。

演習 4

次のベクトルの合計を数値的に求めます。

2 つのベクトルを数値的に加算するには、それぞれの座標を加算する必要があります。

演習 5

次のベクトルの合計を分析的に計算します。

ベクトルを数値的に追加するには、それぞれの座標を追加する必要があります。