ここでは、三角関数の極限を解く方法を学びます。三角関数の極限の例をいくつか確認し、三角関数の極限に関する段階的な演習を解いて練習することもできます。
三角関数の限界とは何ですか?
三角限界は、三角関数で計算される限界です。三角関数の限界を解くには、一般に不定が生じるため、予備手順を適用する必要があります。
さらに、三角関数は周期関数であるため、無限の限界は存在しません。つまり、グラフは特定の値に向かう傾向がなく、定期的に繰り返され続けます。
三角関数の極限公式
すべての三角関数の限界は、次の 2 つの式から計算されます。
![]()
代入によって極限を計算しようとすると、ゼロ間のゼロ不確定性が得られます。
![]()
しかし、この三角関数の公式は、より近い関数の値と x=0 に近い値 (ラジアン単位の角度) を計算することで証明できます。
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(-1)=\cfrac{\text{sen}(-1)}{-1}=0,84147\\[3ex]f(-0,1)=\cfrac{\text{sen}(-0,1)}{-0,1}=0,99833\\[3ex]f(-0,01)=\cfrac{\text{sen}(-0,01)}{-0,01}=0,99998\\[3ex]f(-0,001)=\cfrac{\text{sen}(-0,001)}{-0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ccd668acef73b9140a0cbbb9c1d53ad3_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{c}\begin{array}{l}f(1)=\cfrac{\text{sen}(1)}{1}=0,84147\\[3ex]f(0,1)=\cfrac{\text{sen}(0,1)}{0,1}=0,99833\\[3ex]f(0,01)=\cfrac{\text{sen}(0,01)}{0,01}=0,99998\\[3ex]f(0,001)=\cfrac{\text{sen}(0,001)}{0,001}=0,99999\end{array}\\[14ex]\vdots\\[2ex]\displaystyle\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-66152efc3ce1fa761186a65db677af27_l3.png)
三角関数の 2 つの横方向の極限は 1 なので、点 x=0 での極限は 1 になります。
![Rendered by QuickLaTeX.com \begin{array}{c}\displaystyle\lim_{x\to 0^-}\frac{\text{sen}(x)}{x}=\lim_{x\to 0^+}\frac{\text{sen}(x)}{x}=1\\[3ex]\color{orange}\bm{\downarrow}\\[2ex]\lim_{x\to 0}\displaystyle\frac{\text{sen}(x)}{x}=1\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8af649189957b154866097e315f7cb92_l3.png)
したがって、x が 0 に近づく傾向があるため、x の正弦を x で割った三角関数の限界は 1 に等しくなります。
この公式はいくつかの角度にも適用できます。
![]()
![]()
直接代入によって極限を見つけようとすると、ゼロ間の不定形ゼロが得られます。
![]()
しかし、上の式から等しいことを確認できます。これを行うには、まず分数の分子と分母に 1 と x のコサインを掛ける必要があります。
![]()
分数の分子に注目すべき同一性が得られたので、それを単純化できます。
![]()
![]()
基本的な三角関数の恒等式から始めて、分子を書き換えます。
![]()
![]()
したがって、分数を分数の積に変換できます。
![]()
![]()
限界のプロパティを使用すると、上記の式を限界の積に変換できます。
![]()
上で示した式を使用すると、三角関数の極限を簡単に単純化できます。
![]()
![]()
![]()
そして最後に、結果として得られる制限を計算します。
![]()
したがって、三角関数の極限公式は次のように検証されます。
![]()
他の公式と同様に、複数の角度にも使用できます。
![]()
したがって、三角関数の極限を解くには、算術を使用して関数を変換し、これらと同様の式を取得する必要があります。このようにして、2 つの式のいずれかを使用して、制限値を見つけることができます。
一方で、特定の三角恒等式を適用する必要がある場合もあるため、以下の公式はすべてあなたにお任せします。
3 つの主要な三角比を結び付ける公式:
![]()
基本的な三角関数の恒等式:
![]()
基本的なことから導かれる三角関係:
![]()
![]()
反対の角度:
![]()
![]()
![]()
2 つの角度の合計:
![]()
![]()
![]()
2つの角度の差:
![]()
![]()
![]()
倍角:
![]()
![]()
![]()
半角:
![]()
![]()
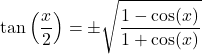
サインとコサインの加算と減算:
![]()
![]()
![]()
![]()
サインとコサインの積:
![]()
![]()
![]()
三角関数の限界がどのように計算されるかを正確に理解できるように、以下に段階的な例をまとめました。
三角関数の限界の例
次の例を使用して、三角関数の極限がどのように解決されるかを見てみましょう。
![]()
三角関数の極限を計算しようとすると、ゼロ間のゼロの不確定性が得られます。
![]()
➤参照: ゼロ間のゼロ制限
したがって、極限を解くために三角関数を変換する必要があります。正接関数はサインをコサインで割ったものに等しいため、次のようになります。
![]()
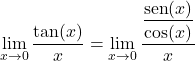
分数の性質を適用することで関数を積として表現できるようになりました。
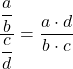
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\displaystyle\frac{\text{sen}(x)}{\text{cos}(x)}}{\displaystyle\frac{x}{1}}=\lim_{x\to 0}{\frac{\text{sen}(x)\cdot 1}{\text{cos}(x) \cdot x}=\\[6ex]\displaystyle =\lim_{x\to 0}{\frac{\text{sen}(x)}{x\text{cos}(x)}=\lim_{x\to 0}\frac{\text{sen}(x)}{x}\cdot \frac{1}{\text{cos}(x)}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-dd10c321c3b7dc40698b318c7187a3c4_l3.png)
限界のプロパティを使用して、2 つの乗算関数の限界を 2 つの限界の積に変換できます。
![]()
上で示したように、最初の三角関数の極限は 1 を与えます。
![]()
![]()
したがって、次の計算を行うだけです。
![]()
三角関数の限界に関する演習を解決しました
演習 1
次の三角関数の極限を解きます。
![]()
まず、直接評価によって三角関数の極限を計算してみます。
![]()
しかし、ゼロオーバーゼロの不確定性が得られます。したがって、関数に変換を適用する必要があります。
まず、次のようにして、分母の x をそのままにしておきます。
![]()
次に、分数を 4 で乗算して除算して、三角関数の限界の最初の式を適用できる式を取得します。
![]()
最後に、最初に示した公式を適用して、三角関数の極限を解きます。
![]()
![]()
演習 2
次の三角関数の限界を計算します。
![]()
まず、三角関数の極限を見つけようとします。
![]()
しかし、不定形ゼロはゼロに達することに対応します。
次に、タンジェントをサインとコサインの商に変換します。
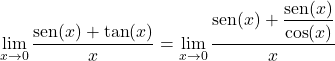
x のコサインを乗算および除算します。
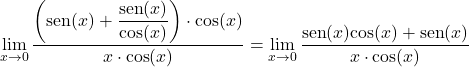
分子に共通因数をとり、三角関数の極限を 2 つに分けます。
![]()
そして最後に、三角関数の極限の結果を求めます。
![]()
演習 3
x がゼロに近づくにつれて、次の三角関数の極限を解きます。
![]()
直接計算を行うことで、0 の間の不定極限 0 が得られます。
![]()
したがって、各項を x の正接で割ることによって極限を単純化します。
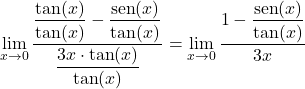
第 2 に、基本的な三角関数の恒等式から、分子の分数が x のコサインに等しいと推定できます。
![]()
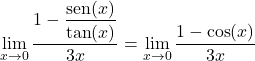
そして、三角関数の極限理論で示されている 2 番目の公式を適用すると、極限を簡単に解くことができます。
![]()
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{1-\text{cos}(x)}{3x}=\lim_{x\to 0}\frac{1}{3}\cdot \frac{1-\text{cos}(x)}{x}=\\[4ex]\displaystyle =\frac{1}{3}\lim_{x\to 0}\frac{1-\text{cos}(x)}{x}=\frac{1}{3}\cdot 0=\bm{0}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b1ee20bc86ad7559fcda3d6bad3c9b27_l3.png)
演習 4
点 x=0 における次の三角関数の極限の解を求めます。
![]()
極限を解こうとすると、不定形 0/0 が見つかります。
![]()
分子の代数式は、倍角の正弦の三角関数の恒等式を使用して書き直すことができます。
![]()
![]()
次に、三角関数の極限を積に分解しましょう。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)\cdot \text{sen}(5x)}{x\cdot x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fc650634075435b782f1e7b921b77c02_l3.png)
そして最後に、限界の特性を適用して三角関数の限界を解きます。
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x\to 0}\frac{\text{sen}(2x)}{x}\cdot\lim_{x\to 0}\frac{\text{sen}(5x)}{x}=\\[4ex]\displaystyle =2\cdot \lim_{x\to 0}\frac{\text{sen}(2x)}{2x}\cdot 5\cdot \lim_{x\to 0}\frac{\text{sen}(5x)}{5x}=\\[4ex]\displaystyle =2\cdot 1\cdot 5\cdot 1=\bm{10}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7c26ba3032828541e69e4bd976ac4f96_l3.png)