絶対誤差と相対誤差は、計算または推定の精度を評価するために使用される 2 つの尺度です。
絶対誤差とは、実際の値と推定値の差を指します。一方、相対誤差は、絶対誤差と実際の値との比率を指します。
どちらも結果の正確性と関連性に関する情報を提供するため、重要です。さらに、工学、物理学、経済学などの多くの分野で広く使用されています。以下にそれぞれについて説明します。
絶対誤差とは何ですか?
絶対誤差は、測定値または推定値と実際の値との差の尺度です。
|測定値 – 実際の値|の式で表されます。 。つまり、絶対誤差は、測定値または推定値と実際の値との差の絶対値です。
数学的な言葉で表現すると、次のようになります。
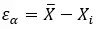
結果の精度とモデルと推定の品質を評価できるため、科学、技術、工学、経済などの多くの分野で基本的な測定であることは言及する価値があります。
絶対誤差はどのように計算されますか?
絶対誤差の計算は簡単です。
測定値または推定値が実際の値から減算され、結果の絶対値が取得されます。
たとえば、実際の値が 10 で、測定値または推定値が 9 の場合、絶対誤差は次のようになります。
|9 – 10| = |-1| = 1。
別の例として、実際の値が 15 で、測定値または推定値が 17 の場合、絶対誤差は次のようになります。
|17 – 15| = |2| = 2。
また、絶対誤差の合計を測定値または推定値の数で割った平均絶対誤差を計算することもできます。計算するには、次の式に従う必要があります。
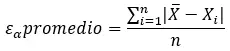
これは、多くの測定値や推定値があり、結果の精度について一般的なアイデアを取得したい場合に役立ちます。
次のような測定値または推定値があるとします。
現在の値: 20
測定値 1:18
測定値 2:22
測定値 3:19
各測定値の絶対誤差を次のように計算します。
絶対誤差 1: |18 – 20| = 2
絶対誤差 2: |22 – 20| = 2
絶対誤差 3: |19 – 20| = 1
平均絶対誤差は次のように計算されます: (2 + 2 + 1) ÷ 3 = 1.67。これは、平均して、測定値または推定値が真の値の 1.67 単位以内であることを示します。
相対誤差とは何ですか?
相対誤差は、真の値に対する絶対誤差の比率による測定または推定の精度の尺度です。
(絶対誤差) ÷ (実際の値)という式で表されます。数学的な言葉で表現すると、次のようになります。
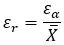
相対誤差は、特に実際の値が異なる場合に、さまざまな測定値や推定値の精度を比較するのに役立ちます。
相対誤差はどのように計算されますか?
相対誤差を計算する場合、絶対誤差は正規化されるため、さまざまな測定値または推定値の精度を実際の値とは独立して比較できます。
たとえば、真の値がそれぞれ 10 と 100、絶対誤差がそれぞれ 1 と 5 である 2 つの測定値または推定値 A と B があるとします。
測定 A の相対誤差は (1) ÷ (10) = (0.1) となり、測定 B の相対誤差は (5) ÷ (100) = (0.05) となります。これは、絶対誤差が大きいにもかかわらず、相対的には測定 B の方が測定 A よりも正確であることを示しています。
相対誤差を計算する方法の例をいくつか示します。
1. 建物の高さを測定すると、100 メートルと推定されます。
測定したところ、実際の長さは98メートルであることがわかりました。
絶対誤差は 2 メートル、相対誤差は (2) ÷ (98) = 0.0204 または 2.04% となります。
2. 物体の重さを測り、その重さが 10 キログラムであると推定するとします。
測ってみると、実際の重さは9.5キログラムだった。
絶対誤差は 0.5 キログラム、相対誤差は (0.5) ÷ (9.5) = 0.0526 または 5.26% となります。
3. ボードの長さを測定すると、それは 200 センチメートルであると推定されます。
測ってみると、実際には201センチメートルであることがわかりました。
絶対誤差は 1 センチメートル、相対誤差は (1) ÷ (201) = 0.00498 または 0.498% となります。
これらの各例では、相対誤差は、絶対誤差と真の値の比という観点から測定精度の尺度を提供します。これにより、実際の値に関係なく、さまざまな測定値と推定値の精度を比較できます。
絶対誤差と相対誤差の違いは何ですか?
絶対誤差と相対誤差は、結果またはモデルの精度を評価するための2 つの異なる尺度です。
絶対誤差とは、量の実際の値または真の値と、推定値または測定値との差を指します。実際の値と推定値の差として計算できます。
絶対誤差 = 実際の値 – 推定値
絶対誤差は、推定値が真の値より大きいか小さいかに応じて、正または負になります。
一方、相対誤差は、絶対誤差と実数値または真の値との関係を指します。これは、絶対誤差と真の値の割合として計算できます。
相対誤差 = 絶対誤差 ÷ 実際の値
相対誤差は通常、パーセントで表されます。このタイプの誤差により、その大きさに関係なく、さまざまな結果やモデルの精度を比較することができます。
たとえば、絶対誤差 1.0 は、少量の重大な偏差である可能性がありますが、大きな偏差ではありません。ただし、どちらの場合でも相対誤差は同じになります。
つまり、絶対誤差は実際の値と推定値の差を測定し、相対誤差は実際の値との関係の観点から推定の精度を測定します。
絶対誤差と相対誤差はどのように応用できますか?
絶対誤差と相対誤差は、次のようなさまざまな分野で広範囲に応用できます。
- 科学– 測定の精度と結果の品質を評価するための科学実験。
- テクノロジー– 機械や装置の精度を評価するための製造および品質管理。
- エンジニアリング– 測定精度を評価し、最終製品の品質を保証するための構築と設計。
- 経済学: 予測の精度を評価し、情報に基づいた意思決定を行うための資産評価と財務リスクの推定。
- 数学と統計: 結果の精度を評価し、モデルを改善するためのモデリングと推定。
絶対誤差と相対誤差の計算例
絶対誤差と相対誤差の両方を計算する 2 つの簡単な例を次に示します。
1. 物体の重量が 3.0 kg と推定され、実際の重量が 2.8 kg であるとします。
絶対誤差は次のように計算します。
絶対誤差 = 実際の値 – 推定値 = 2.8 kg – 3.0 kg = -0.2 kg
相対誤差は次のように計算されます。
相対誤差 = 絶対誤差 ÷ 実際の値 = -0.2 kg ÷ 2.8 kg = -0.0714 または -7.14%
2. コンテナの容積は 50 リットルと推定され、実際の容積は 45 リットルであると仮定します。
絶対誤差は次のように計算します。
絶対誤差 = 実際の値 – 推定値 = 45 リットル – 50 リットル = -5 リットル
相対誤差は次のように計算されます。
相対誤差 = 絶対誤差 ÷ 実際の値 = -5 リットル ÷ 45 リットル = -0.1111 または -11.11%
3. 都市の人口は 100 万人と推定され、実際の数は 975,000 人であると仮定します。
絶対誤差は次のように計算します。
絶対誤差 = 実際の値 – 推定値 = 975,000 – 1,000,000 = -25,000
相対誤差は次のように計算されます。
相対誤差 = 絶対誤差 ÷ 実際の値 = -25,000 ÷ 975,000 = -0.0257 または -2.57%
4. サッカー場の面積が 10,000 平方メートルと推定され、実際の面積が 9,900 平方メートルだとします。
絶対誤差は次のように計算します。
絶対誤差 = 実際の値 – 推定値 = 9,900 – 10,000 = -100 平方メートル
相対誤差は次のように計算されます。
相対誤差 = 絶対誤差 ÷ 実際の値 = -100 ÷ 9900 = -0.0101 または -1.01%
これらの例では、絶対誤差と相対誤差によって推定の精度がわかります。絶対誤差は推定値が真の値からどの程度逸脱しているかを示し、相対誤差は真の値との関係に関して推定がどの程度逸脱しているかを示します。