オイラー数(オイラー定数とも呼ばれる) は、数論、トポロジー、群理論、関数理論など、数学のさまざまな分野において重要かつ不可欠な数学的数です。ギリシャ文字「e」で表され、その近似値は 2.71828 です。
数値 e は指数関数の公式から得られ、複素数理論の基本的な数です。
また、確率の計算や成長と衰退のプロセスのモデル化など、多くの数学的問題を解決する際に現れる自然数でもあります。
オイラー数の由来は何ですか?
オイラー数は、史上最も偉大な数学者の一人であり、現代数学の父と考えられているスイスの数学者レオンハルト オイラー(1707-1783) にちなんで命名されました。
オイラーは、数論、幾何学、微積分学、物理学、天文学を含む数学の多くの分野に貴重な貢献をしました。
対数の計算と理論に関する研究において、数値 e (オイラー数と呼ばれる) を最初に定義して使用したのは彼でした。 オイラーの複素数の公式も、彼の数学への最も注目すべき貢献の 1 つです。
この値はどのようにして得られるのでしょうか?
実際、オイラー数を計算するにはいくつかの方法があります。ただし、どちらの方法でも正確な結果が得られないことに注意してください。したがって、その番号付けは連続的で無限ですが、繰り返されることはありません。
実際、現在、数字 e を構成する数は 1 兆以上知られています。オイラー数を定義する無限級数は次のとおりです。

金 “!”階乗は、その数値までのすべての自然数の積として定義されます。例えば:
5! = 5 4 3 2 1 = 120
この系列は、高さが 1 で幅が減少する一連の長方形の合計としてグラフで見ることができます。ここで、各長方形の幅は 1/n! (n は階乗の数) です。
合計内の長方形の数を増やすと、指数関数の曲線の下の面積の近似値はオイラー数にますます近づきます。
要約すると、オイラー数は無限級数の和から得られる数であり、数学の多くの分野の基礎となります。これは無理数ですが、その近似値は 2.71828 です。
オイラー自身がこの方法を実装して e を小数点以下 18 桁まで計算したことを覚えておくことが重要です。
別の計算方法:
一連の有限項を使用して、直線上のオイラー数の近似値を計算できます。たとえば、上で定義した最初の無限級数を取り上げると、次のようになります。

級数の最初の項を追加することで近似値を計算できます。たとえば、最初の 6 つの項を追加すると、次のようになります。
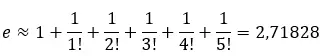
この系列を直線上にプロットして、近似値2.71828 にどのように近づくかを確認できます。
グラフィカルにオイラー数を表す線は、高さが 1 で幅が徐々に減少する一連の長方形として描画できます。ここで、各長方形の幅は 1/n! (n は階乗の数) です。
合計内の長方形の数を増やすと、指数関数の曲線の下の面積の近似値はオイラー数にますます近づきます。
オイラー数を使用した指数方程式
オイラー数を使用した指数方程式は、物理学、生物学、経済学などの科学におけるさまざまな現象をモデル化するために使用できます。ここではいくつかの例を示します。
指数関数的な成長と衰退
このモデルは、人口が増加または減少する速度、または有毒物質が分解される速度を表します。
たとえば、人口が年間 5% の割合で増加している場合、その規模は次の式で表すことができます。
P(t) = P0 · e 0.05t 、ここで P0 は初期母集団サイズです。
放射性崩壊モデル
このモデルは、放射性原子が時間の経過とともに崩壊する速度を表します。
式は次のとおりです。
N(t) = N0 e -λt
ここで、N0 は初期原子数、λ は放射性物質に依存する定数、t は時間です。
これらは、オイラー数を使用した指数方程式が実際にどのように使用できるかを示すほんの数例です。指数方程式が便利で関連性のある分野は他にもたくさんあります。
オイラー数の応用は何ですか?
オイラー数は、数学や科学のさまざまな分野で広範囲に応用できます。数値 e が使用されるフィールドには、次のようなものがあります。
- 計算と数学的分析: 指数関数や対数関数の研究、および微分方程式の解決に使用されます。
- 数論– 素数の分布の研究や数論に関連する問題の解決に使用されます。
- 確率と統計: 確率分布に関連する問題を解決し、期待値を推定する際に使用されます。
- 暗号化– 暗号化および復号化アルゴリズムの研究に使用されます。
- 物理学– 熱力学、量子力学、統計物理学に関連する問題を解決するために使用されます。
- 化学: 化学熱力学および化学反応速度論に関連する問題を解決するために使用されます。
複素数のオイラーの公式
複素数のオイラーの公式は、三角関数と指数関数の間の関係を確立します。式は次のように書かれます。

ここで、「e」は自然対数の底、「i」は虚数単位、「x」は実数、「cos」と「sin」はそれぞれ三角関数のコサインとサインです。
この公式は、数論、関数理論、複素数理論などの数学の多くの分野で非常に役立ち、工学、物理学、経済学にも幅広く応用されています。
実際の使用例はフーリエ解析における信号とシステムの表現にあり、周期信号は複素正弦波信号の合計として表現されます。
オイラーの公式は、これらの複素信号が、個々の正弦波信号を記述する実際の三角関数にどのように関係するかを記述するために使用されます。
オイラー数と複利
複利は、元本と呼ばれるお金の合計が、時間の経過とともに増加する利息に対して利子を得るプロセスを説明する金融概念です。
言い換えれば、投資から得られる利息は、初期資本だけでなく、過去の期間に得られた利息からも得られます。
複利の計算式ではオイラー数が使用されるため、オイラー数と複利には関連性があります。複利の計算式は次のとおりです。
A =パート
ここで、A は最終金額、P は元本、r は金利、t は時間、e はオイラー数です。このように、オイラー数は複利計算の数学的定式化において重要な要素となります。
具体的な数値を使用して複利を計算する例は次のようになります。
1,000 ユーロを 2 年間、年利 5% で投資すると仮定します。複利を計算する式は次のようになります。
A =パート= 1000 e 0.05 2 = 1000 1.1025 = 1102.5 ユーロ。
これは、生成される複利のおかげで、2 年後には当初資本 1,000 ユーロが 1,102.5 ユーロに増加することを意味します。
オイラー数を使った数学的演習の例
以下に、オイラー数を含む数学の問題を解決した2 つの例を示します。
1. 「e ix 」の値を求めます。ここで、x は実数です。
オイラーの恒等式は、e ix = cos(x) + i · sin(x) であることを示します。したがって、x の値がわかっていれば、三角関数を使用して e ixの値を計算できます。
2. 指定された x の値に対して e^(x 2 ) を計算します。
テイラー級数を使用して e^(x 2 ) の値を計算できます。 e xのテイラー級数は無限展開であり、使用される用語に応じて e xの値の逐次近似を計算できます。

この級数の x を x 2に置き換えると、e^(x 2 ) のテイラー級数が得られます。