▷ ゼロ (0/0) 間のゼロ不確定性を解く

この記事では、不確実性が 0/0 になる関数の制限を保存する方法を説明します。さらに、ゼロ間のゼロの不確定性に関する解答済みの演習を使用して練習することができます。

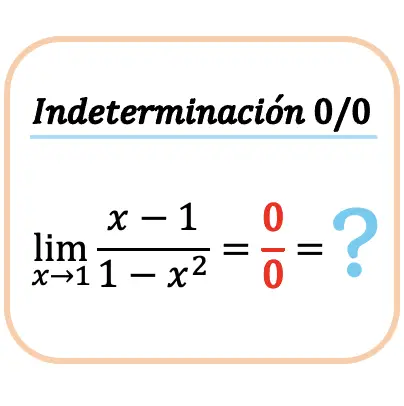
ゼロ (0/0) 間のゼロ不確定性を解く方法

次に、ゼロ (0/0) 間の不確定性がゼロになる関数の極限を計算する方法を見ていきます。これを行うために、例を段階的に計算します。

$\displaystyle\lim_{x \to 2} \frac{x^2-x-2}{x^2-3x+2}$

まず、関数に x の値を代入して制限を計算します。

$\displaystyle\lim_{x \to 2} \frac{x^2 - x -2}{x^2-3x+2}=\frac{2^2 -2-2}{2^2-3\cdot 2+2}=\frac{0}{0}$

しかし、不確定性 0 を 0 で割った値が得られます。

点関数の極限によって不確実性 0/0 が与えられる場合、分子と分母の多項式を因数分解し、共通因数を単純化する必要があります。

したがって、分数の分子と分母の多項式を因数分解する必要があります。これを行うには、ルフィニの法則を使用します。

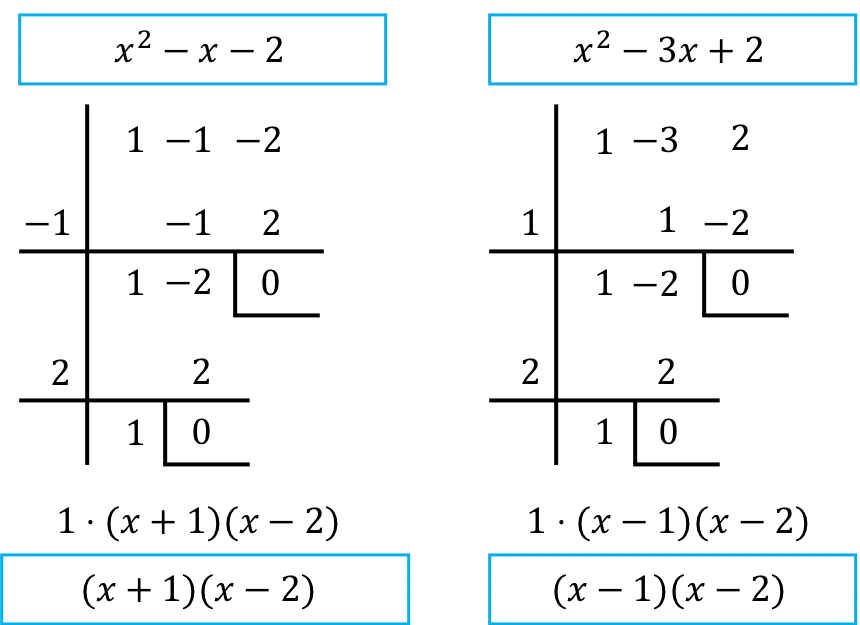
➤多項式の因数分解の方法がわからない場合は、多項式に特化したサイト ( www.polinomios.org)で説明を参照することをお勧めします。

したがって、多項式が因数分解されると、極限は次のようになります。

$\displaystyle\lim_{x \to 2} \cfrac{x^2-x-2}{x^2-3x+2}=\lim_{x \to 2}\frac{(x+1)(x-2)}{(x-1)(x-2)}$

分数の分子と分母で繰り返される因数を削除することで、極限を単純化できます。

$\displaystyle\lim_{x \to 2} \cfrac{(x+1)\cancel{(x-2)}}{(x-1)\cancel{(x-2)}}=\lim_{x \to 2} \cfrac{(x+1)}{(x-1)}$

そして最後に、制限を再計算します。

$\displaystyle\lim_{x \to 2} \cfrac{x+1}{x-1}=\cfrac{2+1}{2-1}=\cfrac{3}{1}=\bm{3}$

ご覧のとおり、多項式を因数分解して単純化すると、極限での解を見つけるのは非常に簡単になります。

根を持つ不確定性 0/0

有理関数の 0/0 の不確定性がどのように解決されるかを見てきました。ただし、極限が無理数 (またはラジカル) 関数の場合、0/0 の不確定性は別の方法で解決されます。

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}$

まず、次の操作を実行して制限を解決しようとします。

$\displaystyle\lim_{x \to 1} \frac{x-1}{\sqrt{x}-1}=\frac{1-1}{\sqrt{1}-1}=\frac{0}{0}$

しかし、ゼロオーバーゼロの不確定性が得られます。

根を持つ関数の極限により不確定性 0/0 が得られる場合、分数の分子と分母に根号式の共役を乗算する必要があります。

➤ 共役は同じ無理数式ですが、中央の符号が変更されていることに注意してください。

次に、分数の分子と分母の両方に根号式の共役を掛けます。

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}$

このタイプの制限内では、このステップを実行することで、簡素化できる注目すべきアイデンティティを常に取得できます。この場合、分母には和と差の積が含まれるため、次のようになります。

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}\right)^2-1^2}$

$\displaystyle\lim_{x \to 1} \frac{\left(x-1\right)\cdot\left(\sqrt{x}+1\right)}{x-1}$

分子と分母で繰り返される因数を単純化します。

$\displaystyle\lim_{x \to 1} \frac{\cancel{\left(x-1\right)}\cdot\left(\sqrt{x}+1\right)}{\cancel{x-1}}=\lim_{x \to 1}\left(\sqrt{x}+1\right)$

このようにして、制限の結果を見つけることができます。

$\displaystyle\lim_{x \to 1}\left(\sqrt{x}+1\right)=\sqrt{1}+1=2$

不確定性に関する演習を解決しました 0/0

以下に、0/0 の不確定性を与える関数の極限について、段階的に解決する演習をいくつか用意しました。それらを実行して、解決策を確認してください。

制限の解決について質問がある場合は、コメント欄で質問できることを忘れないでください。

演習 1

次の有理関数の点 x=-2 における極限を計算します。

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}$

解決策を見る

論理的には、まず制限を解決しようとします。

$\displaystyle\lim_{x \to -2} \frac{x^2 +2x}{x^2-x-6}=\frac{(-2)^2+2\cdot (-2)}{(-2)^2-(-2)-6}=\frac{4-4}{4+2-6}=\frac{0}{0}$

しかし、最終的には 0/0 の不確定性が生じます。したがって、分子と分母の多項式を因数分解する必要があります。

$\displaystyle\lim_{x \to -2}\frac{x^2 +2x}{x^2-x-6}=\lim_{x \to -2}\frac{x(x+2)}{(x+2)(x-3)}$

ここで、分子と分母で繰り返されている括弧を削除して分数を単純化します。

$\displaystyle\lim_{x \to -2}\frac{x\cancel{(x+2)}}{\cancel{(x+2)}(x-3)}=\lim_{x \to -2}\frac{x}{x-3}$

最後に、簡略化された分数を使用して制限を再計算します。

$\displaystyle\lim_{x \to -2}\frac{x}{x-3}=\cfrac{-2}{-2-3}=\cfrac{-2}{-5}=\mathbf{\cfrac{2}{5}}$

演習 2

x が -1 に近づくときの次の関数の極限を解きます。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}$

解決策を見る

まず、いつものように制限を解決しようとします。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3-5(-1)^2+2(-1)+8} =\frac{0}{0}$

しかし、0 と 0 の間の不確定性 0 が得られます。したがって、分数の 2 つの多項式を因数分解する必要があります。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3-5x^2+2x+8}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)(x-2)(x-4)}$

これで多項式を単純化できます。

$\displaystyle\lim_{x \to -1}\frac{(x-1)\cancel{(x+1)}(x+2)}{\cancel{(x+1)}(x-2)(x-4)}=\lim_{x \to -1}\frac{(x-1)(x+2)}{(x-2)(x-4)}$

そして、その限界を解決します。

$\displaystyle\lim_{x \to -1} \frac{(x-1)(x+2)}{(x-2)(x-4)}=\frac{ (-1-1)(-1+2)}{(-1-2)(-1-4)}=\frac{(-2)\cdot (1)}{(-3)\cdot (-5)}=\frac{\bm{-2}}{\bm{15}}$

演習 3

次の根関数の極限の解を求めます。

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}$

解決策を見る

まず、制限によって何らかの不確定性が生じるかどうかを確認します。

$\displaystyle\lim_{x\to 2}\frac{x^2-3x+2}{2-\sqrt{2x}}=\frac{2^2-3\cdot2+2}{2-\sqrt{2\cdot 2}}=\frac{4-6+2}{2-2}=\frac{0}{0}$

この極限により、不確定性ゼロがゼロで除算され、関数内に根が得られます。したがって、分数の分子と分母に根号式の共役を乗算する必要があります。

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{\left(2-\sqrt{2x}\right)\cdot \left(2+\sqrt{2x}\right)}$

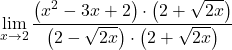
分母は、和と差の積の注目すべき恒等式の展開に対応するため、次のように単純化できます。

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{2^2-\left(\sqrt{2x}\right)^2}$

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}$

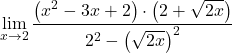
ただし、分数の項を単純化することはまだできません。したがって、多項式を因数分解する必要があります。

$\displaystyle\lim_{x\to 2}\frac{\left(x^2-3x+2\right)\cdot \left(2+\sqrt{2x}\right)}{4-2x}=\lim_{x\to 2}\frac{(x-1)(x-2)\cdot\left(2+\sqrt{2x}\right)}{-2(x-2)}$

このようにして分数を単純化できます。

$\displaystyle\lim_{x\to 2}\frac{(x-1)\cancel{(x-2)}\left(2+\sqrt{2x}\right)}{-2\cancel{(x-2)}}=\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}$

これで、制限の結果を判断できるようになりました。

$\displaystyle\lim_{x\to 2}\frac{(x-1)\left(2+\sqrt{2x}\right)}{-2}=\frac{(2-1)\left(2+\sqrt{2\cdot 2}\right)}{-2}=\frac{1\cdot (2+2)}{-2}=\bm{-2}$

演習 4

次の根関数の x が 0 に近づくときの極限を計算します。

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}$

解決策を見る

まず、いつものように関数の極限を計算してみます。

$\displaystyle\lim_{x\to 0}\frac{x^2+6x}{3-\sqrt{4x+9}}=\frac{0+0}{3-\sqrt{4\cdot 0+9}}=\frac{0}{3-3}=\frac{0}{0}$

しかし、0/0 という不定形が得られます。したがって、関数の分子と分母に無理数式の共役を掛けます。

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{\left(3-\sqrt{4x+9}\right)\cdot\left(3+\sqrt{4x+9}\right)}$

対応する注目すべき恒等式を適用して分母を単純化します。

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{3^2-\left(\sqrt{4x+9}\right)^2}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{9-(4x+9)}$

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

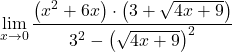
次に、共通因数を取得して分子の二項を因数分解します。

$\displaystyle\lim_{x\to 0}\frac{\left(x^2+6x\right)\cdot\left(3+\sqrt{4x+9}\right)}{-4x}=\lim_{x\to 0}\frac{\bigl[x(x+6)\bigr]\cdot\left(3+\sqrt{4x+9}\right)}{-4x}$

関数の分子と分母で繰り返される因数を単純化します。

$\displaystyle\lim_{x\to 0}\frac{\cancel{x}\left(x+6\right)\left(3+\sqrt{4x+9}\right)}{-4\cancel{x}}=\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}$

そして最後に、関数の制限を解決します。

$\begin{array}{l}\displaystyle\lim_{x\to 0}\frac{(x+6)\left(3+\sqrt{4x+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{(0+6)\left(3+\sqrt{4\cdot 0+9}\right)}{-4}=\\[3ex]\displaystyle=\frac{6\cdot (3+3)}{-4}=\frac{36}{-4}=\bm{-9}\end{array}$

演習 5

0/0 不確定法を使用して次の極限を解きます。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}$

➤参照:関数の横方向の限界を計算する方法

解決策を見る

まず、制限を解決しようとします。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\frac{(-1)^3+2(-1)^2-(-1)-2}{(-1)^3+5(-1)^2+7(-1)+3}=\frac{0}{0}$

しかし、極限ではゼロ対ゼロの不確定性が得られます。したがって、分子と分母の多項式を因数分解します。

$\displaystyle\lim_{x \to -1}\frac{x^3+2x^2-x-2}{x^3+5x^2+7x+3}=\lim_{x \to -1}\frac{(x-1)(x+1)(x+2)}{(x+1)^2(x+3)}$

ここで、分子と分母で繰り返される因子を削除して分数を単純化します。

$\displaystyle\lim_{x \to -1} \cfrac{(x-1)\cancel{(x+1)}(x+2)}{(x+1)^{\cancel{2}}(x+3)}=\lim_{x \to -1}\cfrac{(x-1)(x+2)}{(x+1)(x+3)}$

そして、制限を再度計算します。

$\displaystyle\lim_{x \to -1}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)(-1+2)}{(-1+1)(-1+3)}=\frac{-2\cdot 1}{0 \cdot 2}=\frac{-2}{0} =\infty$

しかし、ここで、数値を 0 で割った値が不確定であることに気づきました。したがって、x が -1 になる傾向がある場合の関数の横方向の限界を計算する必要があります。

まず、左側の点 x=-1 における関数の横方向の極限を解きます。

$\displaystyle\lim_{x \to -1^{-}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{-0}=+\infty$

次に、右側の点 x=-1 における関数の横方向の限界を計算します。

$\displaystyle\lim_{x \to -1^{+}}\frac{(x-1)(x+2)}{(x+1)(x+3)}=\frac{(-1-1)\cdot (-1+2)}{(-1+1)\cdot (-1+3)}=\frac{-2}{+0}=-\infty$

したがって、2 つの横方向の極限が一致しないため、x=-1 における関数の極限は存在しません。

$\displaystyle\displaystyle \lim_{x \to -1^-}f(x)= +\infty\neq\lim_{x \to -1^+}f(x)=-\infty\ \bm{\longrightarrow} \ \cancel{\exists} \lim_{x \to -1} f(x)$

ゼロ間のゼロ不確定性 (0/0)

ゼロ (0/0) 間のゼロ不確定性を解く方法

根を持つ不確定性 0/0

不確定性に関する演習を解決しました 0/0

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする返信をキャンセル

ゼロ (0/0) 間のゼロ不確定性を解く方法

根を持つ不確定性 0/0

不確定性に関する演習を解決しました 0/0

演習 1

演習 2

演習 3

演習 4

演習 5

コメントする 返信をキャンセル

コメントする返信をキャンセル