有理数が他の数とどう違うのか疑問に思ったことはありますか?この記事では、有理数の独自の特徴や分類を含めて、有理数について詳しく説明します。概念をより深く理解する準備をしてください。
有理数とは何ですか?
有理数 (ℚ) は、分数として表現できるすべての数値を含む実数のサブクラスです。これは、有理数とは 2 つの整数の比a/b (b ≠ 0) として記述できる数であることを意味します。
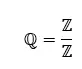
有理数は一連の繰り返しの数字で構成されるため、繰り返しまたは有限10 進数として表すこともできます。有理数の例としては、1/2、3/4、10/3、2/3、π (パイ) などがあります。
有理数のサブセット
有理数は2 つの部分集合に分けることができます。

実数のセットの別のサブカテゴリは無理数であり、これはもう少し複雑です。
有理数の例
有理数とは、分数、つまり 2 つの整数の商として表現できる数です。有理数の例をいくつか示します。
-23
-4/5
-1/2
-7/9
整数を表すすべての分数は同様に有理数です。例えば:
-1/1
-2/2
-3/3
有理数の性質
有理数の主な特徴は、常にゼロ以外の分母を持つことです。
このセットの 2 番目の特性は、各有理数が無限の等価な分数で表現できることです。たとえば、7/2 に等しい有理数 3.5 は、14/4、28/8…、およびその他の無限の分数と書くこともできます。
有理数は分布特性も満たします。これは、ある分数を別の分数で乗算または除算しても結果に影響しないことを意味します。
(a/b) (c/d) = (ac)/(bd)
(a/b)/(c/d) = (ad)/(bc)
有理数の表現
有理数はいくつかの方法で表すことができますが、最も一般的なのは分数として表す方法です。分数は、分子と分母の 2 つの数値で構成されます。
分子は全体のいくつの部分が考慮されるかを示し、分母は全体の中にどれだけの等しい部分があるかを示します。たとえば、ケーキを 8 つの等しいスライスに分割し、そのうちの 3 枚を食べる場合、食べたケーキの量を表す分数は 3/8 になります。
有理数を表すもう 1 つの方法は、 10 進数を使用することです。小数は、分母が数値 10、100、1000 などである分数を記述する簡略的な方法です。たとえば、パイの 1/4 がある場合、これは 0.25 (「全体が 0 で 25/100」を意味します) と表すことができます。
ただし、グラフで表したい場合は、 数直線上に書くこともできます。そうすれば、数字の順序がよくわかります。次に、この行の例を示します。
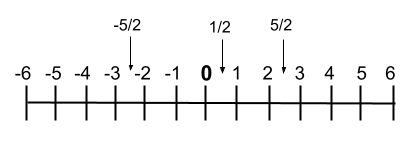
合理的な操作
有理数の基本的な演算は、加算、減算、乗算、除算という整数の演算と同じです。このタイプの演算を解決する方法を学びたい場合は、分数を使用した演算に関する記事を読むことをお勧めします。
ただし、10 進数を基数とする有理数を扱う場合は、 10 進値を扱うときに使用する演算を解く手順に従う必要があります。
有理数の集合に関する結論
この徹底的な説明の後、有理数のセットは数学において最も重要なものの 1 つであると結論付けることができます。分数として表現できるすべての数値が含まれているため、数量を非常に正確に表現できます。