単利は利息を計算する最も一般的な方法で、住宅の購入から個人ローンの借り入れまで、さまざまな目的に使用されます。単利を計算する必要がある場合は、このガイドでその方法を段階的に説明します。作業を簡単にするオンライン計算機も提供しています。
単利計算機
このオンライン単利計算ツールは、単利の計算に関係する変数の計算に役立つツールです。これを使用するには、計算したいものを選択し、要求される変数のデータを入力するだけです。次に、計算ボタンをクリックするだけです。
単利とは何ですか?
単利とは、一定期間、金額を投資または貸与した場合に課される金利のことです。初回金額に金利と期間を乗じて計算されます。要約すると、この利息は継続的かつ通常は短期の金融行為に使用されます。
金利と期間が一定に保たれるため、利息が増加することはなく、毎月または毎年支払わなければならない利息は常に同じです。これが、単利と複利の主な違いです。
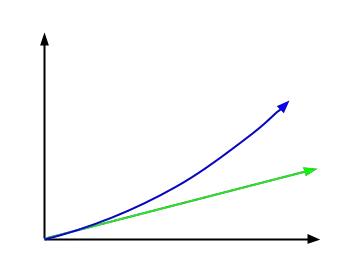
次の図では、単利を表す関数が緑色で示され、複利関数が青色で示されています。画像からわかるように、それははるかに指数関数的な形状をしています。
単利の計算式
単利の計算式はI = C xixtで、次の変数が介入します。
- 初期資本 (C):単利が計算される、投資または貸付された金額の合計。
- 金利 (i):この指標は、時間に対する利子の額をパーセンテージで示します。式に1ずつ書くことが重要です(パーセンテージの値を100で割る)。
- 時間 (t):投資期間の長さ。通常は年単位で表されます。ただし、以下では、月や日などの他の時間単位に変換する方法を説明します。
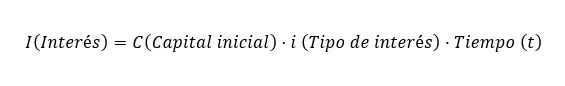
この式がどのように使用されるかを確認するには、次の例を考えてみましょう。年率 4% で 1000 ユーロを投資しました。3 年後にはどのくらいの利息が発生しますか?発生する利息を求めるには、I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = €120 という式を適用する必要があります。
次に、主要な式からさまざまな変数を分離することができ、初期資本、金利、時間、最終資本を計算できる式を取得します。これは次のセクションで説明するもので、すでに見た式と別の非常に簡単な式からこれらの変数を計算する方法を説明します。
最終資本はどのように計算されますか?
最終的な資本を計算するには、ロジックを適用するだけです。そして、最終金額は当初金額と等しいため、利息を適用すると、その式は次のようになります: 最終資本 (Cf) = 当初資本 (C) + 利息 (I)。この式は 2 番目に重要な単利式であり、最も重要なのは前の式です。
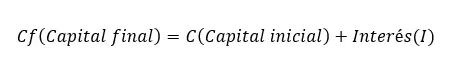
公式がわかったので、次の実際的な例を解いてみてください。50,000 ユーロを 4 年間、利子 20,000 ユーロで投資した場合、最終的に得られる資本はいくらですか?単純に、前の式を適用します: 最終資本 (Cf) = 初期資本 (C) + 利息 (I) = 50,000 + 20,000 = €70,000。
初期資本はどのように計算されますか?
初期資本を計算したい場合は、得られるデータに応じて 2 つの式を使用できます。まず、最終資本と利息によって生成される金額があれば、前のセクションの式を適用できます: 初期資本 (C) = 最終資本 (Cf) – 利息 (I)。
2 番目に、単利計算式 (最初に説明した計算式) で初期資本の価値を分離できます。したがって、初期資本 (C) = 利息 (I) ÷ (時間 (t) x 利率 (i)) が残ります。

2 番目のより複雑なケースの例を見てみましょう。2 年間 8% の金利で 30,000 ユーロの利子を得るにはいくら投資する必要がありますか?初期資本 = I ÷ (tx (i ÷ 100)) という公式を適用すると、30,000 ÷ (2 x (8 ÷ 100)) = €187,500 の初期資金が得られます。
金利はどのように計算されますか?
金利 を計算するには、単利計算式も使用する必要がありますが、i を分離する必要があります。したがって、金利 (i) = 金利 (I) ÷ (初期資本 (C) x 時間 (t)) が残ります。ご覧のとおり、すべての式は同じですが、異なる変数が分離されています。
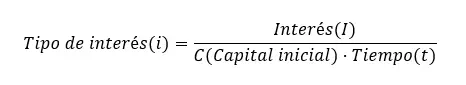
金利計算の実際の例を次に示します。180,000 ユーロを 200,000 ユーロに換算したい場合、5 年間でどのくらいの金利で投資すべきでしょうか?この例では、まず利息を見つける必要があります: I = Cf – C = 200,000 – 180,000 = €20,000。そして、金利 = 20,000 ÷ (180,000 x 5) = 0.022 x 100 = 2.2% を解きます。
時間はどのように計算されますか?
最後に、時間を計算できます。これも最初の式: 時間 (t) = 利息 (I) ÷ (最初の金額 (C) x 利率 (i)) から取得できます。この式では時間の単位が年である必要があることに注意してください。ただし、他の単位で表したい場合は、次の式のバリエーションを使用できます。
- t が年の場合、I = C · (i / 100) · t (一般式)
- I = C · (i / 1200) · t (t が月の場合) (結果は月単位)
- I = C · (i / 36000) · t (t が日の場合) (結果は日)
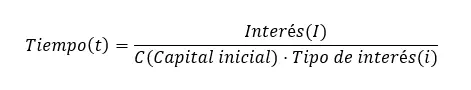
次の例を見てください: 40,000 ユーロの投資で 5,000 ユーロ (金利 5%) の利息が発生する場合、どれくらいの時間が経過する必要がありますか?計算は、時間 = 5,000 ÷ (40,000 x 5 ÷ 100) = 2.5 年のままです。ただし、月単位で計算したい場合は、時間 = 5,000 ÷ (40,000 x 5 ÷ 1200) = 30 月となります。
単利計算の実例
単利計算式を構成する各変数を計算する例を見てきました。ただし、最も一般的な計算の最後の例、つまり重要な計算そのものを示したいと思います。最初の式を適用すると、残りが残ります。計算を確認したい場合は、次のケーススタディを参照してください。
投資のために 10,000 ユーロを借りています。年利 3% を求められた場合、5 年後に返済しなければならない金額を計算したいと考えています。計算は次のようになります。
10,000 × 0.03 = 300
300 x 5 年 = 1,500 ユーロ
CF = 10,000 ユーロ + 1,500 ユーロ = 11,500 ユーロ
したがって、5 年後の利息は 1,500 ユーロとなり、最終的に支払われる資本金は 11,500 ユーロとなります。
結論
要約すると、単利 を計算するには、ローン金額、金利、および期間を考慮する必要があります。そこから、これら 3 つの数値を掛けるだけで、支払われる利息の合計額が得られます。また、利息の代わりに他の変数のいずれかを計算したい場合は、一般式でその値を分離するだけで済みます。