数字のゼロは多くの文化において重要な記号であり、数学や科学でも多くの用途があります。この記事では、数字の 0 の性質、その使用法、歴史などを確認します。読み終えると、その数学的応用、計算での使用方法、そしてその起源がわかります。
数字の0は何を意味しますか?
ゼロという数字は、私たちの番号体系の一部として常に組み込まれていたわけではありません。実際、「ゼロ」という概念は比較的最近の革新です。初期の数値体系には、「何もない」という概念を表す方法がありませんでした。
しかし、算術の発展と、利用可能な記号で表現できるよりも大きいまたは小さい量を表現する必要があるため、ゼロを表す記号が必要になりました。
それは単に量の不在を表す記号として使用されます。これにより、値のない数値を表すことができるため、微積分で非常に役立ちます。
他の数値セットとの関係
ゼロは、いくつかの点で他の数字と関連しています。まず、ゼロは足したり引いたりしても他の数値の値に影響を与えないため、「中立的な」数値と見なすことができます。たとえば、100 は 98 + 2 + 0 に相当します。ゼロは 10 進数の中点でもあります。5 はゼロの右側、-5 は左側です。
ここで注意したいのは、数字 0 は自然数のセットには含まれていないということですが、便宜上含まれる場合もあります。ただし、これは実際にはこのセットや負のセットの一部ではなく、単なる整数であることを知っておくことが重要です。
数字ゼロの性質
ゼロは、数値が存在しないことを示す数学演算子として使用できます。このため、一般に中性元素と呼ばれます。さらに、それは数直線の中心に位置して示されています。これは、負の数と自然数の間の障壁を表すためです。
数学的論理では、これは不在を示すために使用されるため、論理ステートメントがゼロと同等の場合、それはnullであると言われます。そしてコンピューターサイエンスでは、プログラミングのすべての数学で使用される言語であるバイナリコードに意味を与えるため、その使用は不可欠です。
数字のゼロの表現
前に述べたように、数値 0 は数直線の中央に表されます。実際、この値は、負の数 (ゼロ未満) と正の数 (ゼロより大きい) の差を示します。下の画像では、真ん中に数字のゼロがある数直線の表現を見ることができます。
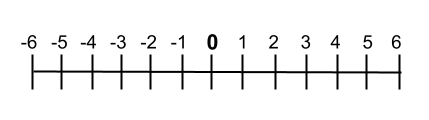
算術演算における数字のゼロ
数字のゼロ 0 は、数量が存在しないことを表す値です。そのため、加算または減算するものが何もないことを示すために数学演算で使用される記号です。単純な概念のように思えるかもしれませんが、数値ゼロの扱いは、乗算と除算においてもう少し複雑です。
足し算や引き算において、0は何も足さない数字であり、結果は変わりません。一方、乗算と除算の演算では、かなりのことが行われます。たとえば、数値にゼロを乗算すると、得られる結果はゼロになります。数値が何であっても、結果は常に 0 になります。
一方、ゼロを任意の数値で割ると0 が得られ、その逆の操作を行うと結果は無限になります。 0 ÷ 0 という演算を実行しない限り、不確定性が生じます。ご覧のとおり、ゼロによる除算は、前の演算よりもわずかに複雑な演算です。
0番の物語
数字のゼロは世界のさまざまな地域で独自に発明されました。ゼロが最初に使用されたのはインドであると信じている歴史家もいますが、バビロンであったと主張する歴史家もいます。明らかなことは、ゼロという数字は人間が発明したものであり、固有の意味を持たないということです。
ゼロの発明は数学の発展における基礎的な一歩であり、今日の世界のあり方に大きな影響を与えました。ゼロがなければ、数値と数学的演算は大きく異なります。実際、ゼロは現代の微積分に意味を与えていると言っても過言ではありません。
興味深いのは、古代のギリシャの数学者は計算にそれを使用しなかったことです。しかし、マヤ人はそれを使用しており、7 世紀にヨーロッパにそれを紹介したのはヒンズー教の数学者ブラフマグプタでした。
それ以来、ゼロは人類にとって非常に重要なものとなり、現代のテクノロジーを促進してきました。
現在、ゼロは数学と科学において非常に重要です。物理学では、絶対零度は可能な限り低い温度です。化学では、 pH スケールのゼロは完全に酸性の溶液を表します。そして、コンピューティングでは、 2 進ゼロがすべての数値と数値計算の基礎となります。
さらに、ゼロは日常生活においても重要です。電話番号と住所はゼロがなければ同じではありません。そしてもちろん、ゼロがなければデジタル時計や電卓は存在できません。数字の 0 についてすべてがわかったところで、どう思いますか?