古代以来、一連の自然数は数学の多くの分野を構築する基礎となってきました。たとえば、算術や幾何学はこれらの数値に基づいています。そのため、この短い記事では、自然数の定義とこの集合に関連するすべての概念について説明します。
自然数とは何ですか?
自然数は、物理世界のオブジェクトを数えたり順序付けするために使用する一連の抽象的な要素です。数学では、自然数の集合は一般に文字 ℕ で表されます。これは、小数を含まず小数ではないすべての正の整数で構成されます: ℕ = {1, 2, 3, 4, 5, 6…}。
言い換えれば、自然数とは、実際のオブジェクトを数えるために使用できるすべての正の整数です。このように、数字 1 は実際の物体を数えるのに使用できるため、自然数であると言えます。たとえば、リンゴ 1 個と梨 2 個で、合計 3 個の果物ができます。
次の画像では、すべての数値セットをまとめた図を示し、セット ℕ がどこにあるかを確認できます。そして、自然数の概念をよりよく理解するために、それは他のものとどのような関係を持っていますか。説明を続ける前に、コンセプトマップをよく見て理解することをお勧めします。

数値が自然数かどうかはどうやってわかりますか?
すでに述べたように、自然数は数えたり順序付けしたりするために使用される数です。値が自然かどうかを知るには、次の点に留意する必要があります。数値 ℕ には負の符号がないこと、小数点以下の桁がないこと、虚数単位がないこと、分数ではないことです。次に、最初の 100 個の自然数のリストを示します。
1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、17、18、19、20、21、22、23、24、25、 26、27、28、29、30、31、32、33、34、35、36、37、38、39、40、41、42、43、44、45、46、47、48、49、50、 51、52、53、54、55、56、57、58、59、60、61、62、63、6 4、65、66、67、68、69、70、71、72、73、74、75 、76、77、78、79、80、81、82、83、84、85、86、87、88、89、90、91、92、93、94、95、96、97、98、99、100 。
自然数はどのように読み書きされるのでしょうか?
自然数は 10進数体系に従います。これは、値の算術基数が 10 であることを意味します。すべての数字は、1、2、3、4、5、6、7、8、9 の 9 桁のうちの少なくとも 1 つで構成されます。また、自然数には小数点や負の符号が決して存在しないことを覚えておいてください。 。
すべての算術演算に関する限り、これらの数値は数学的表記法に従って記述されます。記号や式について疑問がある場合は、この最後のリンクにアクセスして記事を読むことをお勧めします。そこには、数学言語とすべての表記に関するすべての情報が見つかります。
自然数の特徴
自然数の最も重要な特性のいくつかは次のとおりです。
- 0 は自然数ではないので、最初の自然数は 1 になります。
- 測定、制御、計算に使用されます。長さ、重量、容量などの測定に使用できます。
- それらは互いに比較することができ、どちらが他の自然数より大きいか小さいかを知ることができます。
- 自然数には順序があります。自然数は 1 から始まり無限大で終わる論理的な順序に従います。
- 2 つのナチュラルは同じ後継者や同じ前任者を持つことはできません。
- 自然数は小数や分数ではなく正の整数であるため、すべての自然数は整数です。
このセクションの締めくくりとして、学生の間でよく疑問を引き起こすこのセットに関する一連の説明を残しておきます。数字のゼロは自然数ではない、自然数は整数である、自然数は負の数であってはなりません、自然数には小数点がありません場所もあり、自然数も無限です。
自然数の表現
ℕ とも呼ばれる自然数のセットは、1、2、3、4… などの正の整数で形成されます。この集合は次の表記法で表されます: ℕ = {1, 2, 3, 4, 5…}。ただし、 数直線上に配置することで、よりグラフィカルに表現することもできます。
この 2 番目の方法では、まっすぐな水平線を引き、その線に沿って自然数の値を整然と書きます。セットの順序を簡単に視覚化できるため、このシステムはこの数値セットを学習する人にとって非常に適しています。次の図では、行のレイアウトがどのように見えるかを示しています。
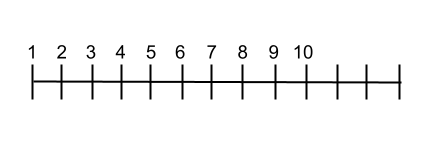
自然数を使った演算
集合 ℕ の特性とプロパティをすべて理解したので、次はこれらの数値の主な応用である算術演算にそれらを適用します。次に、基本四則演算(足し算、引き算、掛け算、割り算)について詳しく説明します。
自然値を加算すると、別の数値 ℕ が得られます: 3 + 6 = 9 。ただし、自然数間の減算を行うと、結果は正の数または負の数になる可能性があります。後者は私たちが話している集合に属していないため、正の結果が得られる減算のみが集合 ℕ の一部となります: 4 – 2 = 2 。
自然数間の乗算の場合は、正の数のみが得られるため、加算の場合と同じです。たとえば、3 と 8 を掛けたい場合、 3 · 8 = 24となります。しかし、集合 ℕ 内の数値間で除算すると、場合によっては10 進数を取得できます。この状況では、結果は自然全体の一部ではありません。
したがって、自然数の集合では、加算と乗算のみが定義されます。これら 2 つの操作は、可換性と結合性のプロパティをチェックします。したがって、初期数が自然数であれば、結果は常に自然数になります。このように、集合 ℕ の性質を常に尊重した演算となります。
自然数の応用
自然数は日常生活でよく使われます。たとえば、テーブルの長さや人が店まで歩くのにかかる時間を測定するために使用できます。また、加算や減算などの数学的計算を実行するために使用することもできます。整数は、棚に本を置くなど、空間内のオブジェクトの位置を決定するために使用することもできます。