数学的記法は、記号を使用してアイデアや計算を伝える方法です。一見するとわかりにくいかもしれませんが、少し練習すれば簡単に解釈できるようになります。この記事では、この表記で使用されているすべての記号の意味と、それらを適用する方法の例をいくつか示します。
数学的記法とは何ですか?
数学的記数法は、数学で使用される値や式を記述する方法です。このテクニックにより、数学者はアイデアを簡潔かつ正確に述べることができます。数学の表記法を使用すると、数学を実践または研究する人が概念をよりよく理解できるようになります。
数学の言語を、数値を記述する方法である科学表記法と混同しないでください。一方、数学的表記法は、言語と同様に、複雑な式を記述できる一連の記号です。この件については後ほど詳しく説明します。
数学表記をどう読むか?
数学的表記の解釈を学ぶことは、思っているよりも簡単です。各記号の意味を学ぶだけでよく、一度理解すれば、数学的表記で書かれたものは何でも読めるようになります。とてもシンプルですが、明らかに練習と多くの学習時間が必要です。
数学的表現は非常に論理的であり、常にパターンに従っています。そのため、ルールを暗記するだけで、それをどのような状況にも当てはめることができます。非常に複雑な計算を記述することもできます。これは数学言語の魔法であり、非常に複雑なメッセージを体系的に伝えることができます。
数学表記の構成要素
数学的表記は、数値、演算、およびそれらの間の関係を表す一連の記号で構成されます。これらの記号は最初は複雑に見えるかもしれませんが、少し練習して理解すれば、数学的表記を解釈するのは子供の遊びになるはずです。
次に、数学言語に含まれる 4 種類の要素について詳しく説明します。最も基本的なものから始まり、最も複雑で抽象的なもので終わります。そして、理論的な説明が終わったら、存在する数値表記の種類について話します。
数値と数値セット
まず第一に、数学的数値を定義する必要があります。これは、単位に関連する量を指定する数学的概念です。 10 進数体系に従い、記号 0、1、2、3、4、5、6、7、8、9 を組み合わせて、任意の数値を記述することができます。
さまざまなプロパティに従って数値を並べ替えると、数値セットと呼ばれるいくつかのカテゴリの数値が得られます。また、これらの値のグループには、それらを指定する独自の記号もあります。次のリストでは、それらすべてを対応するグループの名前とともに示します。
これらの記号は通常、広範囲の数値を一度に決定するために計算で使用されます。たとえば、それに応じて多くの値を受け入れる式がある場合、数値を 1 つずつ記述する代わりに、数値グループに対応する記号を使用してこれらの値を指定する方が簡単になります。
演算子と量指定子
数学の本質である数値について説明したので、演算子と量指定子についても説明する必要があります。 1 つ目は、加算 (+)、減算 (-)、乗算 (x または ·)、除算 (÷) など、演算を表すためのすべての記号です。
ただし、論理演算子と関係演算子という他の 2 種類の演算子もあります。 1 つ目は結合、分離、否定を表します。これらは、算術演算とは異なり、数値ではなく数学的命題を扱う論理演算を提案するのに役立ちます。
2 番目の方法では、値または数式間の等価性と関係を確立できます。これらの記号は算術計算 (数値の順序付け) で使用できますが、代数では変数がある場合により重要です (これについては 2 つのセクションで詳しく説明します)。
次のリストでは、これまで説明したすべての演算子の定義を確認できます。
| シンボル | 意味 | 親切 |
| + | 追加 | 算術演算子 |
| – | 引き算 | 算術演算子 |
| バツ、 *、 ・ | 乗算 | 算術演算子 |
| ÷ | 分割 | 算術演算子 |
| x² | 権限付与 | 算術演算子 |
| √ | デポジット | 算術演算子 |
| そして | 接続詞 | 論理演算子 |
| どちらか | 論理和 | 論理演算子 |
| いいえ | 拒否 | 論理演算子 |
| = | に等しい | 関係演算子 |
| > | より大きい | 関係演算子 |
| < | より小さい | 関係演算子 |
| >= | それ以上か同等 | 関係演算子 |
| <= | 以下 | 関係演算子 |
| ≠ | に等しくありません | 関係演算子 |
| ≡ | まったく同じ | 関係演算子 |
| ≈ | ほぼ等しい | 関係演算子 |
| ≃ | に相当 | 関係演算子 |
| ∝ | 比例 | 関係演算子 |
他にも 5 つの論理演算子がありますが、これらは集合論から数学的論理を説明するために使用されます。計算、幾何学、統計などで使用されるセット ロジックを適用するブランチです。次に、使用される記号とその定義を示します。
| シンボル | 意味 |
| x ∈ A | xはAに属します |
| x ∉ A | x は A に属しません |
| ∪ | 連合 |
| ∩ | 交差点 |
| ⊂ | インクルージョン |
数量詞については、特定の条件(等価性、順序、メンバーシップなど) を満たす集合の要素の数を示す記号として定義できます。演算子にはさまざまな種類がありますが、最もよく使用される演算子を以下に挙げます。
| シンボル | 意味 | 親切 |
| ∀x | すべてのx | 定量化する |
| ∃x | 少なくとも 1 つの × があります | 定量化する |
| ∄x | ×はありません | 定量化する |
| ∃!x | ×が一つだけある | 定量化する |
| | | のような | 定量化する |
| ∴ | それで | 定量化する |
数学式とその関係
これまで取り上げてきた記号を使用すると、多くの数学を理解できますが、組み合わせ演算や代数計算などの複雑な式での応用や関係についてはまだ説明していません。さらに、議論すべき関係のシンボルがまだあります。これらについては、このセクションで説明します。
グループ化記号から始まり、括弧、角括弧、中括弧です。これらの要素は、複雑な式を指定する場合に不可欠です。その主な機能は、グローバル式内で特定の計算を優先することです。そして、3 つのタイプの間には異なる優先順位があります。この式では、書き込み順序 3 {[2 + (3 – 2) · 2] – 4} がわかります。
| シンボル | 意味 | 優先度 |
| “(”そして”)” | 括弧 | 最大優先度 |
| “[“そして”]” | ブラケット | 二番目の優先順位 |
| “{” そして “}” | キー | 3番目の優先順位 |
このカテゴリの最後に、加算と乗算の繰り返しを記述するための要素である和 (Σ)と積 (∏)について説明します。合計は、「i が 1 から an までの値を取る Xi の合計」と言うのと同じです。そして積は同じですが、足すのではなく掛け算します。
代数解析
代数記号について最初に説明するのは、アルファベットで表される変数です。それらの機能は数値を模倣することですが、数学定数のような固定値を持たないため、新しい値を取ることができます。これは方程式、極限、導関数、積分、行列などに適用されます。
最後に、この最後の段落で説明したすべての代数演算の表現について話したいと思います。それ以来、それらは代数学の基礎となっており、その記号が何であるかを知る必要があります。次に、さまざまな記号と簡単な定義を示す表を示します。
| シンボル | 意味 |
| リムx → b | 限界 (x が b に向かう傾向があるとき) |
| y’、ƒ’ (x)、dy / dx | 派生関数 |
| ∫ | 完了 |
| MXNへ | mxn 次元の行列 |
数学言語の記号に関する結論
ここまで、数学で扱われる重要な記号をすべて見てきましたが、明らかにさらに議論すべきことがあります。しかし、これらは数学の各サブカテゴリー、幾何学、統計学、代数学にもっと固有です… したがって、この主題は終了し、数値表記について説明します。
数値表記の種類
このセクションでは、さまざまな表記法があるため、数学的な数値を表現するすべての方法を見ていきます。冒頭で、数学者が最もよく使用する 10 進数体系について触れました。次に、これをさらに詳しく説明し、他のタイプの数学表記を示します。
10進数表記
10 進数体系は、位置記数体系 (各桁の位置によって値が決まる体系) であり、数値 10 の倍数と約数に基づいています。10 は数値の基数として使用される数値であるためです。したがって、使用する 10 個の数字記号は、1、2、3、4、5、6、7、8、9、0 です。
これらの数値の値は、位置に応じて確立された、桁の合計に 10 を底とするべき乗を乗じて決定されます。また、1 未満の数値を記述するには小数点を使用する必要があることを覚えておくことが非常に重要です。以下に例を示します。
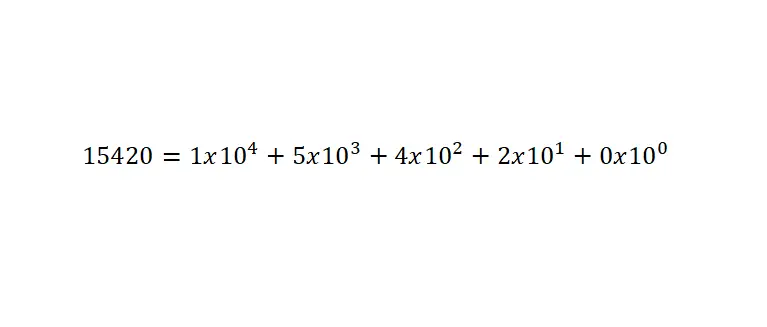
科学的表記法
指数形式表記または科学表記は、明らかに科学と技術で最もよく使用される記述タイプの 1 つです。実際、これにより、非常に大きな数と非常に小さな数を簡単な方法で表現できるようになります。科学的表記法の定義を理解するために、この表記法に整数を渡す方法を説明します。
- 小数点を移動します。最初の桁に到達するまで、必要なだけ小数点を移動する必要があります (数値が非常に大きい場合は左に、数値が非常に小さい場合は右に)。
- 底を確立します。この最後の数値に 10 を掛けたものを書きます。つまり、小数点を片側に移動して得た値の隣に、10 を掛けた「x 10」を書きます。
- 指数を追加します。小数点を移動した回数と同じ値を指定します。大きな数値の場合は指数を正のままにしますが、小さな数値の場合は負の符号を付けて記述する必要があります。
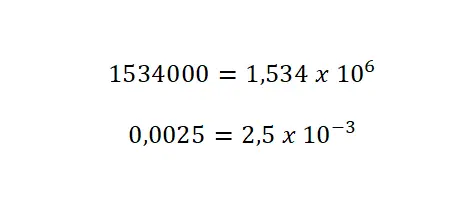
16進数表記
16進法は 16 に基づいており、16 の異なる記号を使用することを意味します: 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、Fこの番号付けシステムは、10 進法の数字と 6 つの文字で構成されています。この表記は一般に、特に IT および IT に関連するすべての分野で使用されます。
他のタイプの表記法と共通の記号があるため、括弧とインデックス 16を使用して 16 進数で書かれていることを常に示す必要があることを明確にすることが重要です。次の例では、16 進数から 10 進数への変換が非常に明確な例で示されています。
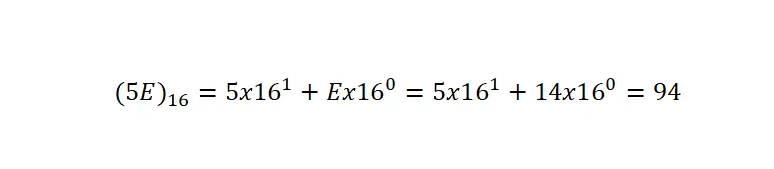
16 進数を 10 進数の式に変換するには、10 進表記で行ったように、数値を基数の乗算に分解する必要がありますが、基数を 16 に変更します。次に、各桁に、その特定の桁が占める位置から 1 を引いた 16 を乗算します。
8進数表記
最後に説明するシステムは、8 を基数とする 8進表記です。これは、0、1、2、3、4、5、6、7 の 8 つの記号または数字のみを使用することを意味します。これは最も使用されません。これまで説明してきたすべての番号付けシステム。この表記の変換は、以前の表記と同じ手順に従って実行されることに注意してください。
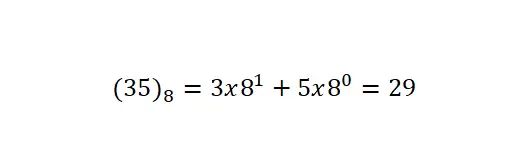
小説表記
最後に、ローマ数字の体系について話します。これは現在ではあまり使用されていませんが、過去には数学の分野で非常に重要でした。それは数学に命を吹き込んだ記法の 1 つだったからです。
記述できる記号は 7 つまでに制限されています: I (1)、V (5)、X (10)、L (50)、C (100)、D (500)、M (1000)。これらの文字を組み合わせると、すべての数字が書き出されます。これらがどのように結合されて他のより大きな数が生じるかを知りたい場合は、最後のリンクからアクセスして、それらに関する記事を読むことをお勧めします。
数学表記の読解パフォーマンスを向上させるにはどうすればよいですか?
数学表記を読み取るパフォーマンスを向上させる方法はいくつかあります。 1 つの方法は、記号や数字を声に出して読むことです。もう 1 つの方法は、シンボルとその意味をよく理解することです。練習問題や問題を使って数学表記を読む練習もできます。
このガイドがお役に立てば幸いです。ご質問がございましたら、お気軽にコメントに書き込んでください。または、このトピックに関して貢献したい場合は、コメント欄にもその旨を記載していただければ幸いです。そうは言っても、読み続けたい場合に備えて、数学の学習方法に関する記事を残しておきます。