関数変換: 変換、拡張、対称

このページでは、関数変換とは何か、およびその検索方法について説明します。変換には、平行移動 (または変位)、対称、および拡張 (または収縮) の 3 つのタイプがあります。また、疑問を残さずに練習して概念を理解できるように、段階的に解決される演習も用意されています。

関数変換とは何ですか?

場合によっては、すでに知っている他の初等関数とよく似た初等関数をグラフ化するように求められることがあります。同様の関数を再度表現する代わりに、テクニックを使用して、ある関数の表現から別の関数の表現に簡単かつ迅速に切り替えることができます。

したがって、関数変換は、基本的な操作を通じて、ある関数のグラフィック表現から別の非常によく似た関数のグラフィック表現への移行を可能にする技術です。

基本的に、初等関数の変換には 3 つのタイプがあります。

平行移動または移動: 関数は垂直方向と水平方向に移動できます。
反映または対称: X 軸または Y 軸を対称軸として使用して、関数を反映できます。
拡大・縮小: 関数を拡大・縮小することができます。

関数の変換の概念を理解したら、それぞれの種類の変更をさらに詳しく見ていきます。

関数の変換または移動

まずは機能のシフトから始めます。縦方向の翻訳と横方向の翻訳の 2 種類があります。

関数の平行移動または垂直移動

関数を垂直方向 (Y 軸に沿って) に平行移動または移動するには、関数に定数を加算または減算する必要があります。

関数に ka を追加することで、関数をk 単位上に移動します。

$\bm{f(x)+k}$

関数から ka を減算して、関数を k 単位下にシフトします。

$\bm{f(x)-k}$

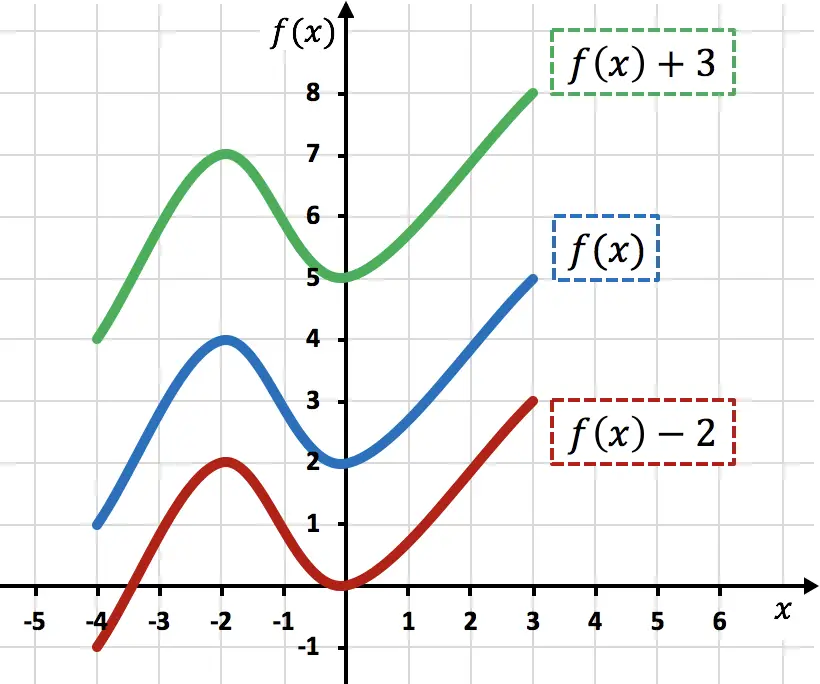
グラフからわかるように、関数に定数を追加すると、追加される単位が上にシフトします (緑色の関数)。一方、関数から数値を減算すると、減算された単位が下に移動します (赤色の関数)。

このタイプの移動では、ファンクションポイントの Y 座標のみが変更され、X 座標は同じままであることに注意してください。

関数の平行移動または水平移動

関数を水平方向 (X 軸に沿って) に移動またはシフトするには、独立変数xに定数を加算または減算する必要があります。

のグラフ

$\bm{f(x+k)}$

のグラフです

$f(x)$

k単位を左に移動しました。

のグラフ

$\bm{f(x-k)}$

のグラフです

$f(x)$

k単位を右にシフトしました。

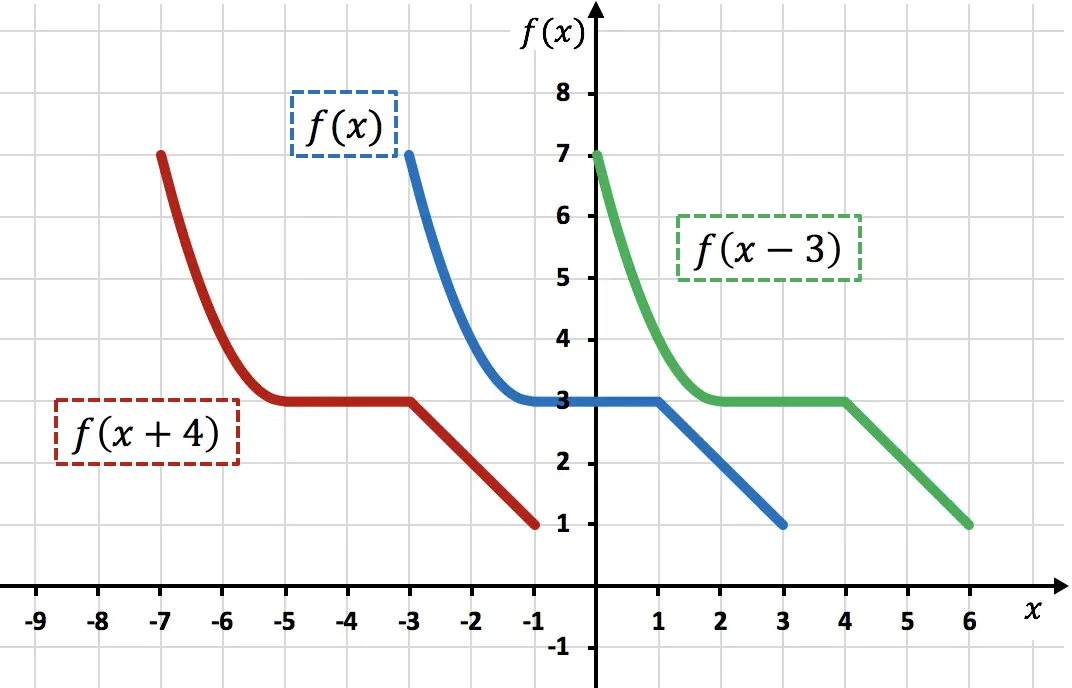
グラフからわかるように、定数を変数xに直接追加すると、関数は追加された単位を左にシフトします (赤い関数)。一方、変数xから数値を減算する場合、関数は減算された単位を右にシフトします (緑色の関数)。

このタイプの移動では、ファンクションポイントの X 座標のみが変更され、Y 座標は同じ値を維持することに注意してください。

関数の変換または移動の例

次の関数を上に 4 単位、右に 3 単位移動します。

$f(x)=x^2$

関数を 4 単位上に移動するには、関数に 4 単位を追加する必要があります。

$f(x) + 4 = x^2 + 4$

また、関数を右に 3 単位移動するには、計算する必要があります。

$f(x-3)$

。したがって、

$x$

我々はできる

$x-3 :$

$f(x-3) = (x-3)^2 + 4$

したがって、上に 4 単位、右に 3 単位シフトした関数は次のようになります。

$\bm{f(x) = (x-3)^2 + 4}$

以下に、元の関数と変換された関数をグラフ化して、それらの違いを確認します。

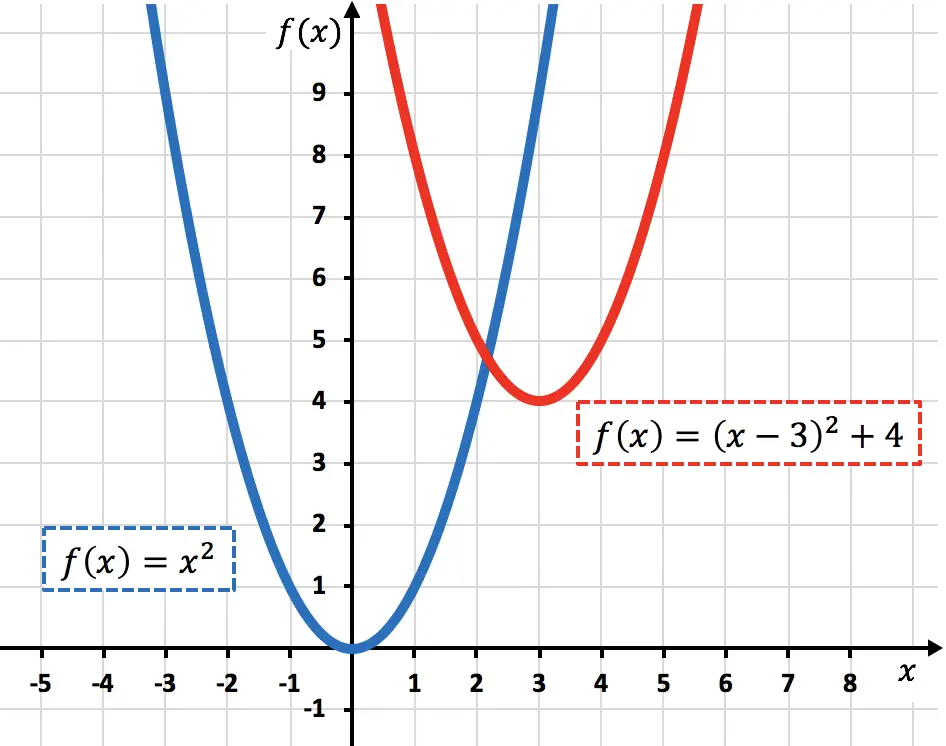
数学者によっては、両方のタイプの動きが同時に発生する場合、斜めの変位または平行移動と呼びます。

座標軸に対する関数の鏡映または対称性

次の方法で、任意のデカルト軸に関して対称関数を表すことができます。

X 軸に関して関数を反映するには、関数の符号を変更する必要があります。つまり、計算する必要があります。

$\bm{-f(x)}.$

y 軸に関して関数を反映するには、独立変数xを否定する必要があります。つまり、次を計算する必要があります。

$\bm{f(-x)}.$

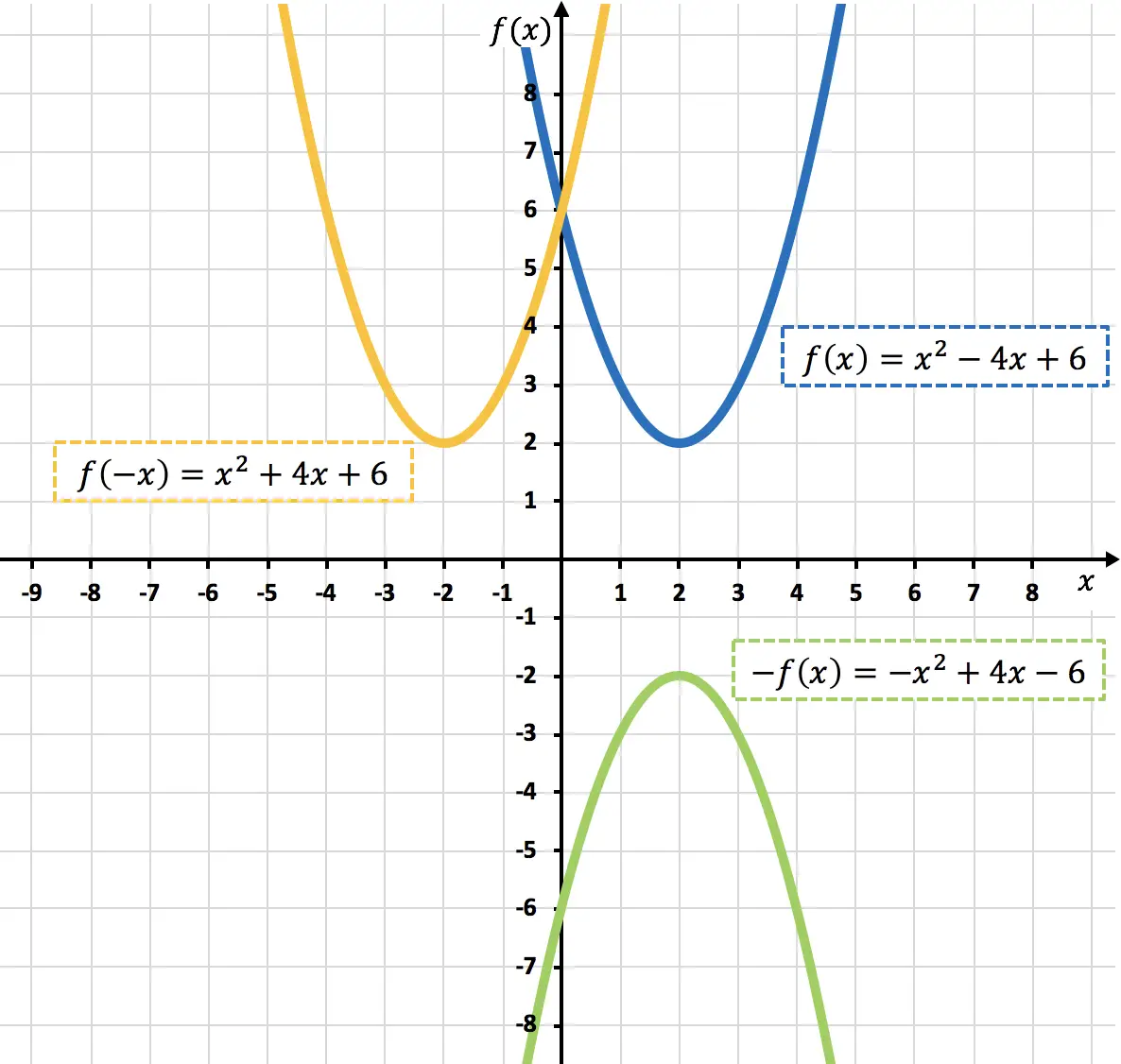
前のグラフでわかるように、関数に -1 を乗算することで、関数をグラフィカルに反転します (オレンジ色の関数)、言い換えれば、X 軸に対してミラーリングします。

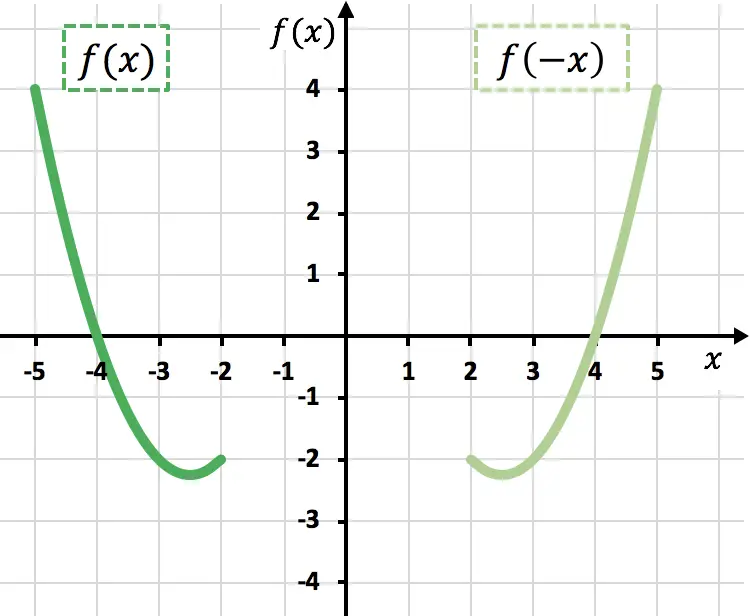
前のグラフでわかるように、変数xを否定することで、Y 軸に関して関数をミラーリングします (薄緑色の関数)。

関数のミラーリングの例

次の二次関数の OX 軸を中心とした対称関数と OY 軸を中心とした対称関数を計算します。

$f(x)=x^2-4x+6$

X 軸に関して対称な関数を見つけるには、次のようにする必要があります。

$-f(x)$

$-f(x)=-\bigl[x^2-4x+6\bigr]$

$\bm{-f(x)=-x^2+4x-6}$

そして、Y 軸に関して対称な関数を見つけるには、次のことを行う必要があります。

$f(-x)$

。したがって、ある場所を置き換えます。

$x$

元の関数では項によって

$-x :$

$f(x)=x^2-4x+6$

$f(-x)=(-x)^2-4\cdot (-x)+6$

$f(-x)=x^2-4\cdot (-x)+6$

$\bm{f(-x)=x^2+4x+6}$

以下に、元の関数と見つかった対称関数の両方を表します。

関数の拡張と縮小

翻訳と同様に、拡大または縮小には垂直方向と水平方向の 2 つのタイプがあります。

関数の垂直方向の伸縮

整数関数に係数を乗算すると、関数を拡大または縮小できます。

Y 軸上の関数を拡大 (または拡張) するには、関数に 1 より大きい数値を乗算する必要があります。

$kf(x)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> <p style=$ Y 軸上の関数を縮小するには、関数に 1 未満の正の数を掛ける必要があります。

$kf(x)\qquad 0</div> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="http://mathority.org/wp-content/uploads/2023/07/expansion-et-contraction-d-une-fonction.webp" alt="expansion et contraction verticales d'une fonction" class="wp-image-320" width="442" height="438" srcset="" sizes="" data-src=""></figure> </div> <p> Comme vous pouvez le voir dans le graphique précédent, si on multiplie une fonction par un coefficient supérieur à 1 (fonction verte) on la rend plus grande le long de l’axe OY, en revanche, si on multiplie une fonction par un coefficient supérieur à 0 mais plus petit que 1 (fonction rouge), nous le rendons plus petit le long de l’axe OY.</p> <h3 class="wp-block-heading"> Expansion et contraction horizontales d’une fonction</h3> <p> Dans ce cas, au lieu de multiplier la fonction entière par un coefficient, pour qu’une fonction se dilate ou se contracte horizontalement, nous devons multiplier la variable indépendante <em>x</em> . </p> <div style="padding-top: 23px; padding-bottom: 0.5px; padding-right: 30px; padding-left: 30px; border: 2px dashed #FF9B28; border-radius:20px;"> Pour <strong>étendre (ou dilater) une fonction sur l’axe X,</strong> il faut multiplier tous les <em>x</em> par un nombre compris entre 0 et 1 :” title=”Rendered by QuickLaTeX.com” height=”392″ width=”2425″ style=”vertical-align: -4px;”></p> <p> f(kx)\qquad 0</p> <p style=$ X 軸上の関数を縮小するには、すべてのxに 1 より大きい数を掛ける必要があります。

$f(kx)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> </div> <div class=$

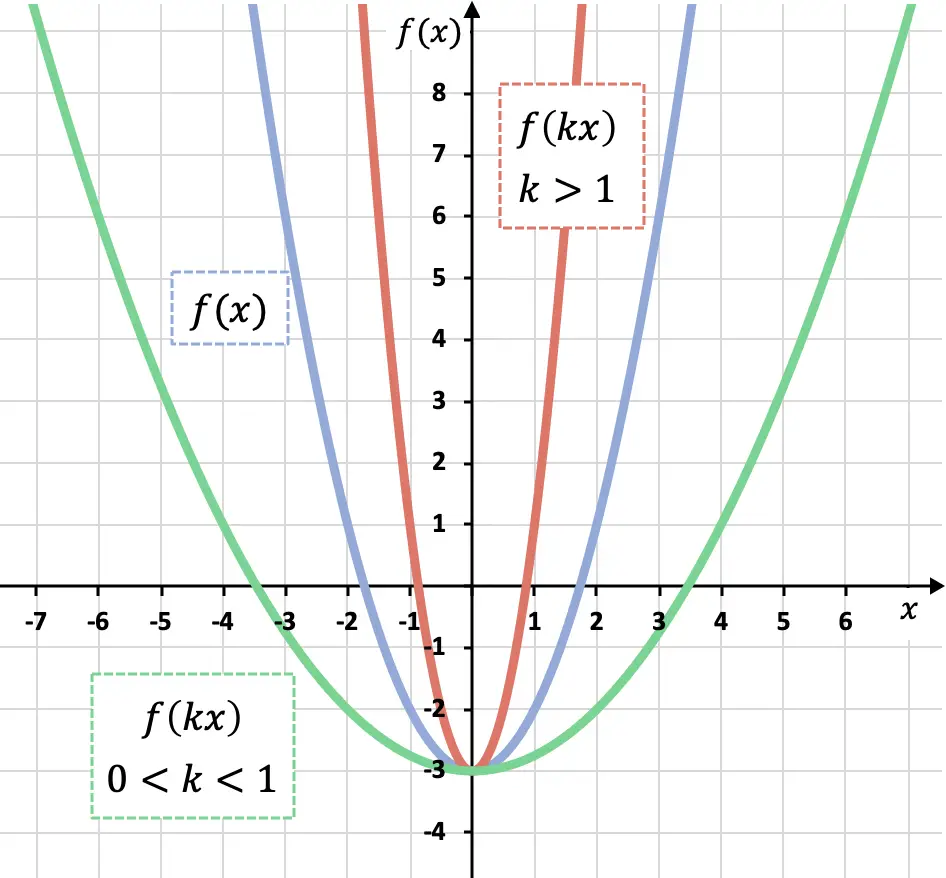
前のグラフでわかるように、関数のすべてのxに 0 より大きく 1 未満の係数を掛けると (緑の関数)、OX 軸に沿って拡大されます。 1 より大きい係数による関数 (赤色の関数) を OX 軸に沿って縮小します。

関数を展開または折りたたむ方法の例

次の無理関数を垂直方向と水平方向に複製します。

$f(x)=\sqrt{9-x^2}$

y 軸上の関数を 2 倍に拡張するには、関数全体を 2 倍する必要があります。

$2f(x)=2\sqrt{9-x^2}$

また、関数を x 軸で 2 倍に拡張するには、関数のすべてのxに次の値を乗算する必要があります。

$\displaystyle \frac{1}{2}:$

$\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}$

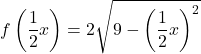
したがって、2 つの座標軸上で複製される関数は次のようになります。

$\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}$

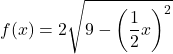
以下に、元の関数と変換された関数をグラフで示し、それらの違いを確認します。

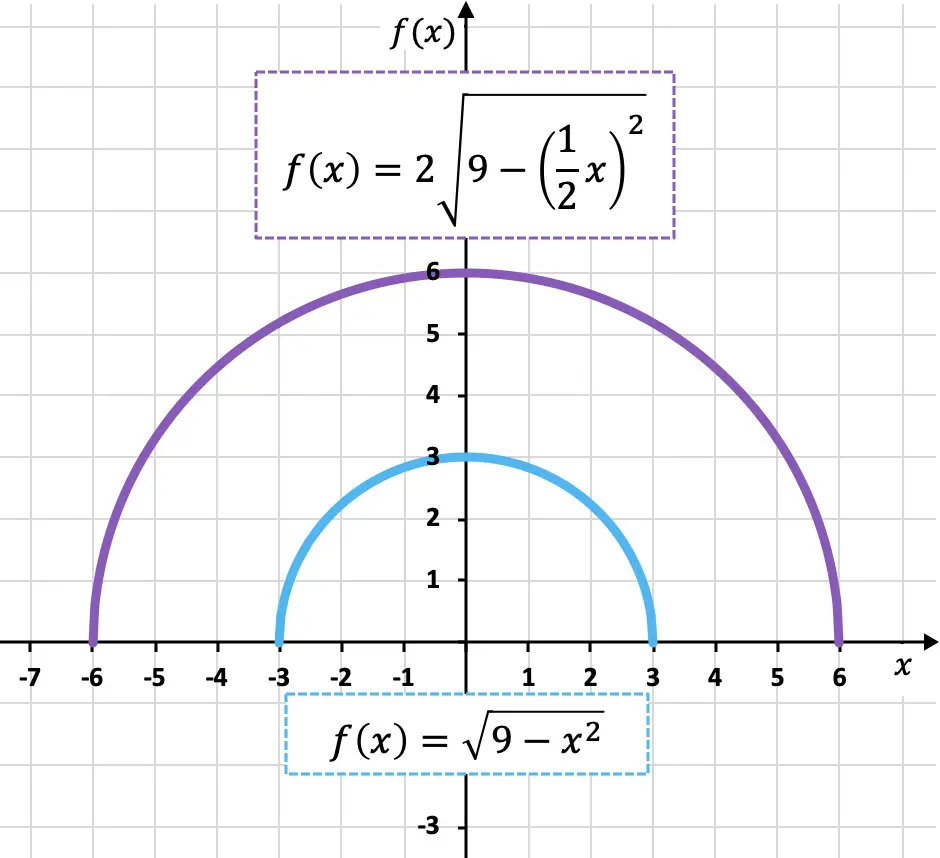
ご覧のとおり、新しいフィーチャ (紫色) は元のフィーチャ (青色) の縦方向と横方向の両方で 2 倍の大きさになっており、フィーチャが拡張されています。

関数変換に関する演習を解決しました

演習 1

次の 3 次関数を 5 単位上に移動します。

$f(x) = 4x^3-9x-2$

解決策を見る

関数を 5 単位上に移動するには、関数に 5 を追加します。

$\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}$

したがって、5 単位シフトされた関数は次のようになります。

$\bm{f(x) = 4x^3-9x+3}$

演習 2

次の二次関数の Y 軸を中心とした対称関数を求めます。

$f(x) = 2x^2-3x+6$

解決策を見る

Y 軸に関して対称な関数を見つけるには、次の計算が必要です。

$f(-x)$

つまり、置き換える必要があります

$x$

のために

$-x$

関数内:

$f(-x) = 2(-x)^2-3\cdot (-x)+6$

$f(-x) = 2x^2+3x+6$

したがって、OY 軸に関する対称関数は次のようになります。

$\bm{f(x) = 2x^2+3x+6}$

演習 3

次の関数の水平圧縮をその表現の 3 分の 1 に実行します。

$f(x) = x^3-4x^2-5x+1$

解決策を見る

機能を削減するには、

$f(3x) = (3x)^3-4(3x)^2-5(3x)+1$

$f(3x) = 27x^3-4\cdot 9 x^2-15x+1$

$f(3x) = 27x^3-36 x^2-15x+1$

したがって、縮小された関数は次のようになります。

$\bm{f(x) = 27x^3-36 x^2-15x+1}$

演習 4

4 単位右に変換された次の関数の OX 軸に関する対称関数を計算します。

$f(x) = 3x^3-x^2+5x+8$

解決策を見る

対称関数を計算する前に、まず関数を右に 4 単位移動する必要があります。したがって、次のようになります。

$f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-12$

そして関数を移動したら、X 軸に関して対称な関数を計算します。これを行うには、取得した関数を否定する必要があります。

$\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]$

$-f(x) = -3(x-4)^3+(x-4)^2-5x+12$

つまり、すべての基本操作を適用した後の関数は次のようになります。

$\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}$

演習 5

次の関数を左に 2 単位シフトしてから、垂直方向に 4 倍に拡張します。

$f(x) = x^4-5x^3-x-3$

解決策を見る

まず、関数を 2 単位左に移動します。

$f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-2-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-5$

次に、係数 4 を使用して関数を Y 軸に沿って展開します。

$4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]$

$f(x) = 4(x+2)^4-20(x+2)^3-4x-20$

結論として、すべての基本変換を適用した後の関数は次のようになります。

$\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}$

演習 6

関数から

$f(x)=x,$

グラフ上のどの表現が関数に対応するかを決定する

$f(x)=x-3 .$

解決策を見る

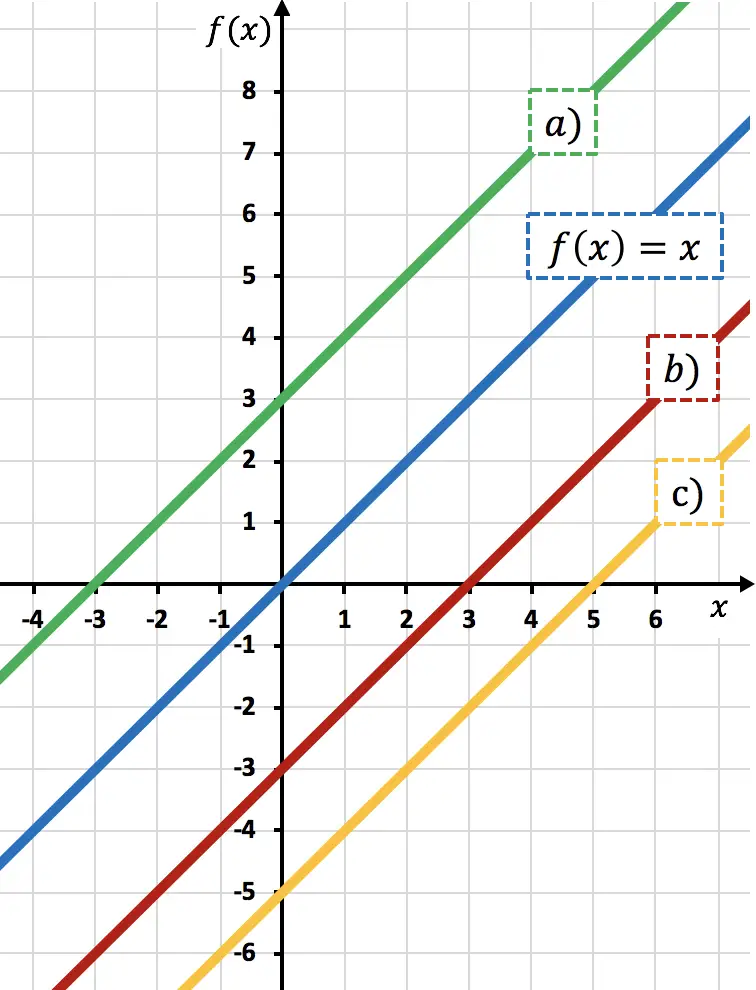
関数

$f(x)=x-3$

関数です

$f(x)=x$

3ユニット下に移動しました。関数から数値を引くと、関数が下に移動するためです。

したがって、次の表現は、

$f(x)=x-3$

線 b)に対応します。これは、線と比較して 3 単位下にシフトしているためです。

$f(x)=x .$

これは縦軸を見るとわかります。

$f(x)=x$

が 0 を通過すると、赤い線は -3 を通過するため、3 単位下にシフトされます。

演習 7

関数から

$f(x)=x^2+2,$

どの放物線が関数を表現しているかを決定する

$f(x)=(x-6)^2+2 .$

解決策を見る

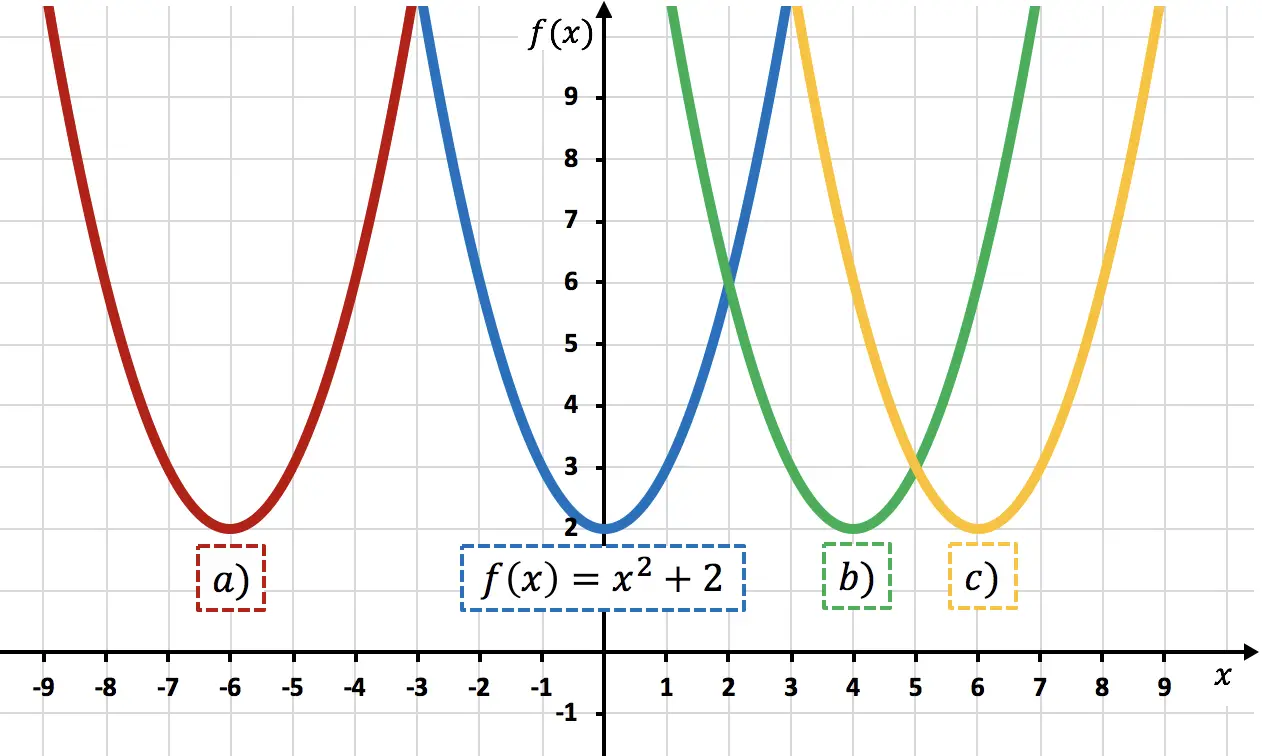
関数

$f(x)=(x-6)^2+2$

関数です

$f(x)=x^2+2$

6ユニット右に移動しました。これは計算して確認できます

$f(x-6):$

$f(x)=x^2+2$

$f(x-6)=(x-6)^2+2$

したがって、次の表現は、

$f(x)=(x-6)^2+2$

放物線 c)に相当します。これは、放物線 c) と比較して右に 6 単位シフトしているためです。

$f(x)=x^2+2$

。

これは、放物線の頂点を見るとわかります。放物線の頂点間の距離です。

$f(x)=x^2+2$

放物線 c) の頂点は 6 単位なので、後者は最初のものと比較して右に 6 単位シフトします。

関数変換: 平行移動、対称、拡張、圧縮

関数変換とは何ですか?

関数の変換または移動

関数の平行移動または垂直移動

関数の平行移動または水平移動

関数の変換または移動の例

座標軸に対する関数の鏡映または対称性

関数のミラーリングの例

関数の拡張と縮小

関数の垂直方向の伸縮

関数を展開または折りたたむ方法の例

関数変換に関する演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

コメントする返信をキャンセル

関数変換とは何ですか?

関数の変換または移動

関数の平行移動または垂直移動

関数の平行移動または水平移動

関数の変換または移動の例

座標軸に対する関数の鏡映または対称性

関数のミラーリングの例

関数の拡張と縮小

関数の垂直方向の伸縮

関数を展開または折りたたむ方法の例

関数変換に関する演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

コメントする 返信をキャンセル

コメントする返信をキャンセル