Magic Squares は、楽しくエキサイティングな方法で計算スキルを訓練する数学パズル ゲームです。だからこそ、これは若い学生に数学を教えるための最良のリソースの 1 つです。
マジック アレイとは何ですか?また、それはどのように解決されますか?
魔方陣は、整数が書き込まれる、さまざまなボックスで構成される一種のテーブルまたは行列です。ただし、いかなる状況でもインストールすることはできません。一連のルールは遵守する必要があります。
- すべてのマジックサム (水平、垂直、または対角線のすべての値の合計) は、常にマジック定数と同等の値 (単一の値) を与える必要があります。
- どの数値も 2 回繰り返すことはできません。
- 使用できるのは、連続する数字 (たとえば、1 から 9)、または特定の系列に続く数字 (たとえば、奇数、5 の倍数など) のみです。
また、正方形はその構造に応じてさまざまに分類できることを強調することが重要です。 1 つ目は正方形の次数に応じたもので、行または列にあるセルの数に相当します。 2 つ目は、テーブルの次数の種類 (偶数または奇数) に応じて異なります。これらの区別から、すべての正方形をさまざまなカテゴリに分類できますが、これについては後で詳しく説明します。
魔方陣の解き方は?
この数学ゲームを解決するには、幾何学を使用するか、魔法の定数を計算するという 2 つの異なる方法を使用できます。どちらの手順も同様に有効ですが、一方の手順ではより迅速に結果を得ることができますが、もう一方の手順ではより多くの時間と推論が必要になります。次に、両方の方法について説明しますので、好みの方法を選択して、それぞれの状況にうまく適応できます。
魔方陣の公式は何ですか?
最初の方法は、魔法の定数を計算することで構成されます。これには次の式を使用する必要があります: n(n 2 +1)/2 (n は二乗の次数)。この値を取得したら、あとはさまざまな数値の組み合わせを試すだけです。これにより、正方形全体のマジック サムを定数に等しくすることができます。言い換えれば、全体のバランスがとれるように、合計が定数の値になる数値の組み合わせを形成する必要があります。
幾何学を使用して魔方陣を解くにはどうすればよいですか?
次に、 geometryを使用して魔方陣を解くことができます。ただし、この方法は非常に単純であり、純粋に系統的であるため、計算スキルを発揮する必要がないことに注意してください。ということで、偶数次マスと奇数次マスの両方を解く手順を説明します。
奇数の魔方陣を解くにはどうすればいいですか?
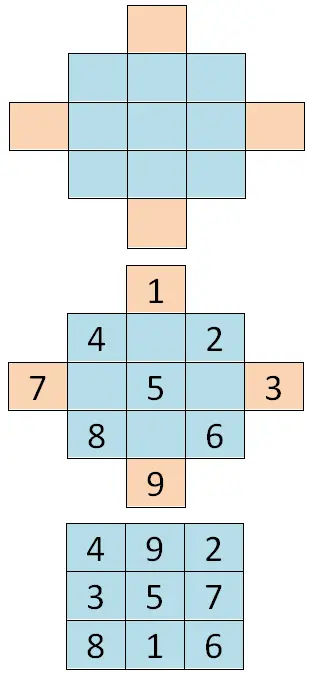
この最初のケースを解決するには、最初のテーブルにセルを追加して、一種のダイヤモンドを作成する必要があります。次に、一連の最初の桁 (この場合は 1) から始まるすべての連続する数字を書き、ひし形の対角線に沿って書きます。最後に、数値を「2倍」にする必要があるため、外側のセルの値は反対側に移動します。したがって、垂直軸の外側のセルが交差すると、水平軸のセルでも同じことが起こります。以下に例を示します。
偶数次の魔方陣を解くには?
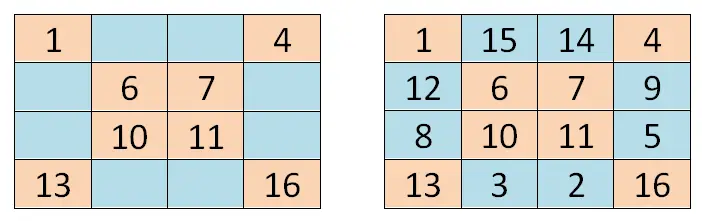
偶数次の魔方陣(偶数の行と列を持つ魔方陣) を解くには、前の方法とは多少異なる方法を使用できますが、これも幾何学に基づいています。まず、シリーズの最初の番号 (この場合は 1) を左上隅に書き込みます。次に、2 つの主な対角線をトラバースし、各ボックスの位置に対応する値を書き込みます。
2 つの主な対角線を書き終えたら、右下隅から始まる最初の空のボックス (この場合はボックス 15) に配置する必要があります。そこに系列の 2 番目の値を書き込み、残りの値を順番に (最小から最大まで) 書き込み、セルを右から左、下から上に完成させます。より明確にするために、以下に示す画像を見てください。
魔方陣の作り方は?
自分で魔方陣を構築するには、いくつかの手順に従うことができますが、そのうちの 2 つを取り上げます。それぞれが異なるタイプの正方形を作成するために使用されるため、生成したい正方形に応じて方法を慎重に選択する必要があることに注意してください。
シャム法
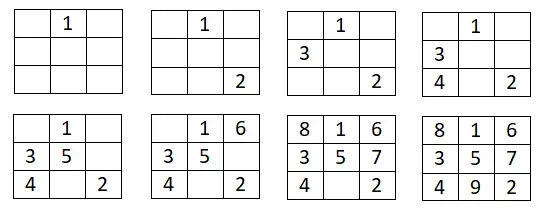
この最初の方法は非常に簡単で、特に任意のサイズの奇数の魔方陣を構築するのに役立ちます。従う手順は非常に簡単です。基本的には、最初の行の中央のボックスにシリーズの最初の番号を書き込みます。そこから、選択した等差数列の順序に戻り、次の数値を上と右に書き込みます。ただし、この位置が描画された正方形の外側にある場合は、最後の行または列に移動する必要があります。そして、完全な正方形になった場合は、最後に入力した数字の正方形から 1 つ下に移動し、同じ方法を続行する必要があります。
以下に 3×3 の例を示します。
Strachey の魔方陣法
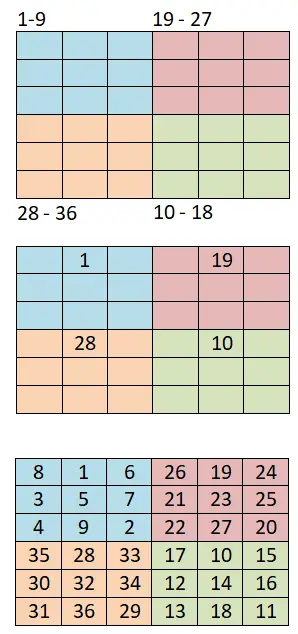
次数 4k + 2 ペアの魔方陣を生成するには、この別の方法を使用します。これは、前の方法 (シャム方法) に基づいており、これも非常に簡単です。以下に、従うべき手順と 6×6 の魔方陣の実際の例を示します。
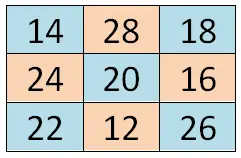
- より小さな象限に分割する:最初に行う必要があるのは、ボードを小さな正方形に分割することです。たとえば、6×6 のボードがある場合は、3×3 の正方形からなる 4 つの等しい象限を作成する必要があります。
- シャム法を使用します。次に、各小さな象限に数値の範囲を割り当てます。たとえば、シーケンスを 1 で開始する場合、範囲は 1 ~ 9 (最初)、10 ~ 18 (4 番目)、19 ~ 27 になります。 (2位)、28-36(3位)。
Conway の魔方陣に対する LUX 法
次数4n + 2 (n は自然数) の魔方陣を生成する場合は、後者のシステムを使用します。したがって、このスタイルの正方形を作成する手順は次のとおりです。
- テーブルまたは行列の作成:まず、次数 2n + 1 の行列を作成します (n は自然数)。これでテーブルを設計できるようになり、その次数を念頭に置いて設計を開始します。
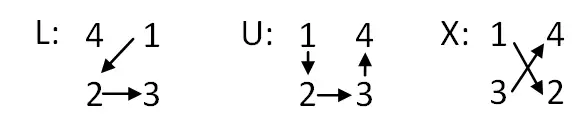
- 文字の配置:表を作成したら、上から下に、L を n + 1 行、U を 1 行、X を n – 1 行と書く必要があります。その後、U を交換する必要があります。真ん中にLが付いています。
- 文字を数値に置き換える:次に、文字を 4 つの連続する数字のグループに置き換える必要があります。文字に応じて、番号に何らかの順序を付けます。以下で説明します。
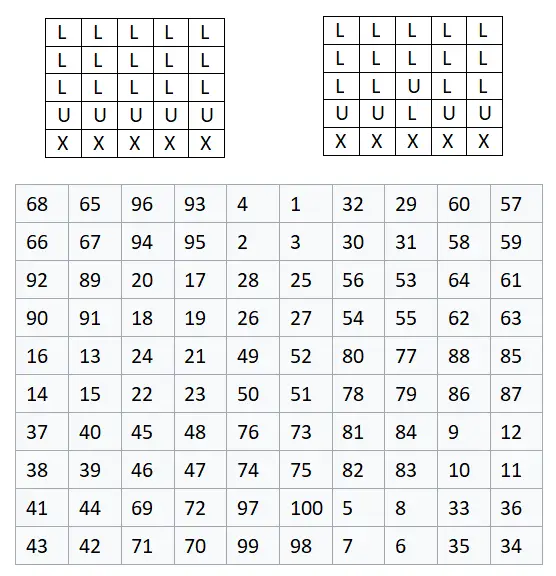
5×5 行列を構築することから始めます。つまり、2n + 1 = 2 · 2 + 1 = 5 であるため、n = 2 となります。これは、行列のサイズが最終的に 10×10 になることを意味します。すでに述べたように、文字を含む各セルは 4 つの数字のグループ、つまり 2×2 の行列に相当します。以下に完成した例を示します。この例では、各文字が、画像に示されている順序で 4 つの数字のグループに置き換えられています。
魔方陣の練習
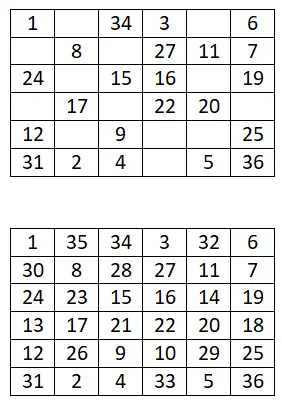
次に、不完全な魔方陣をいくつか提供します。この記事で説明した概念に従って、自分でそれらを埋める必要があります。教えられたどの方法でも使用できることを覚えておいてください。さらに、1 は宣言に含められますが、シリーズの最初の数字ではない可能性があることを考慮する必要があります。演習の 1 つを完了すると、ステートメントの下に解決策が表示されます。
3×3の魔方陣
奇数のみを使用して 3×3 の魔方陣を作成します。
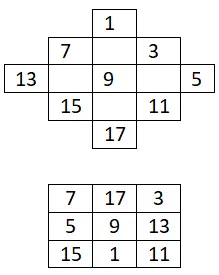
4×4の魔方陣
次の 4×4 の魔方陣を完成させます。
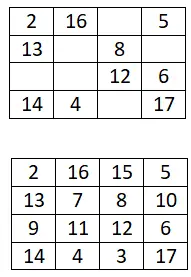
5×5の魔方陣
次の 5×5 の魔方陣を完成させます。
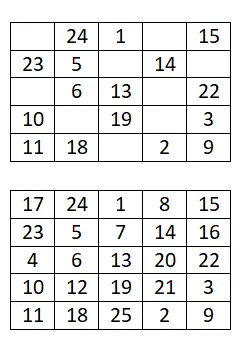
6×6の魔方陣
次の 6×6 の魔方陣を完成させます。