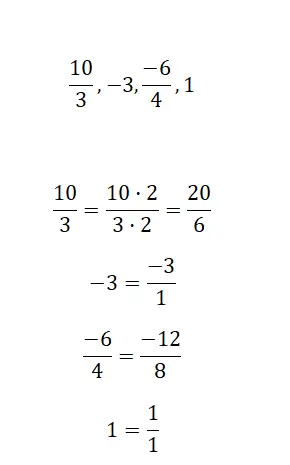この記事では等価分数や等分数についての解説が充実していて分かりやすいです。より具体的には、それらの定義、計算方法、および 2 つの分数が等しいかどうかを確認する方法について説明します。こうすることで、最後に紹介するような等価分数の練習問題を解くために必要なすべてを知ることができます。ということで、本題から始めましょう。
等価分数計算機
この等価分数計算ツールを使用すると、計算を行わずに 2 つの分数が等しいかどうかを確認できます。操作は非常に簡単で、基本的には2つの分子と2つの分母に相当する値を入力して「計算」ボタンを押すだけです。
等価分数とは何ですか?
等価分数とは、同じ数値を表す分数のことで、分子と分母が違っても同じ結果となる分数です。これは、それらが比例関係にあることを意味し、増幅または単純化の 2 つのタイプがあります。次に、概念をよりよく理解できるように、等価分数の図例を示します。
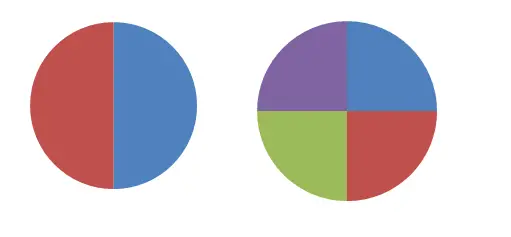
前の画像では、2 つの円が 2 つと 4 つの部分に分割されていることがわかります。最初の図を分数で定義しようとすると、各部分は全体の 1/2 に等しいと言えますが、2 番目の図では分数 1/4 を使用します。明らかに、これら 2 つの分数は異なる量を表すため、等価ではありません。しかし、2 番目の円 (2/4) を 2 つ取ると、この式は 1/2 に相当します。
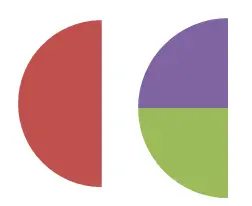
この 2 番目の画像では、 1/2 と 2/4 が等価であることがわかり、数値的にも検証できます。 1/2 = 0.5 および 2/4 = 0.5 なので。以前にコメントした定義によれば、2 つの分数が同じ数値を表す場合、それらは等価な分数です。
相当する分数の例
ここで、等価な分数の例を 5 つ示します。それらの計算方法を理解したい場合は、読み続けることをお勧めします。
- 半分に相当する分数: 2/4、3/6、4/8 など。
- 3 分の 1 に相当する分数: 2/6、3/9、4/12 など。
- 4 分の 1 に相当する分数: 2/8、3/12、4/16 など。
- 1 に等しい分数: 4/4、7/7、15/15 など。
- 5 分の 1 に相当する分数: 2/10、3/15、4/20 など。
同等の分数を計算するにはどうすればよいですか?
同等の分数を取得するには、分子と分母に同じ数値を乗算または除算する必要があります。分数の両方の部分を同じ方法で変更すると、比例関係が維持されるためです。したがって、増幅と縮小の 2 つの方法を使用できます。
増幅によって等価な分数を見つける
この最初のケースでは、最初の分数に特定の数値を掛ける必要があります。これは、分子と分母にこの数値を掛ける必要があることを意味します。例で確認できるように、乗算を実行した後に得られる 2 つの等価な分数を以下に示します。
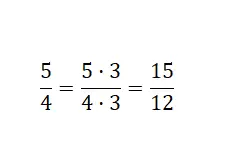
私たちが行ったのは、分数の両方の部分に 3 を掛けることでした: 5 x 3 = 15 と 4 x 3 = 12 。したがって、増幅された等価部分が得られます。これは、それが大きいためです。結論として、元の分数と同じ量を表す、異なる数値から構成される分数が見つかりました。
単純化によって等価な分数を求める
2 番目に、特定の分数の分子と分母を割ることによって分数を単純化することを選択できます。このようにして、最初のものよりもさらに単純な、別の等価な分数を取得します。ただし、この方法は、最初の式が既約分数でない場合にのみ機能することに注意してください。後者はそれ以上約分できないためです。以下にリダクション(簡略化)による等価分数の計算例を示します。
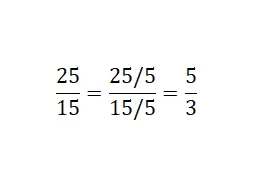
図からわかるように、私たちが行ったことは、分数の分子と分母の両方を公約数で割ることです。この例では、25/5 = 5 および 15/5 = 3 の 5 つを使用しました。最後に、25/15 の既約同分数を取得しました。
2 つの分数が等しいかどうかはどうやってわかりますか?
同等の分数を特定するには、以下で説明する 3 つの手順のいずれかに従う必要があります。 2 番目は、前のセクションで説明した分数の簡略化に関連していることに注意してください。
分子と分母の乗算
2 つの分数間の等価性を確認したい場合は、この最初の手順を使用できます。基本的に、最初の分数の分子に 2 番目の分数の分母を掛ける必要があります。次に、2 番目の分数の分子に最初の分数の分母を掛ける必要があります。両方の結果が同じである場合、これらの分数は等しいことになります。次の例を見てください。
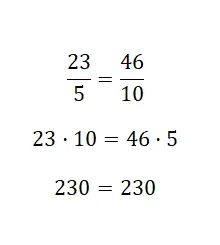
この最後の例では、2 つの分数が等しいことを検証しました。この例は、2 番目の分数が最初の分数の 2 倍である、つまり増幅された等価関係があるため、分かりやすかったです。この手順は非常に使いやすく、十字を掛けるだけで十分であることに注意してください。ただし、より多くの数学的リソースを自由に使えるようになるため、他の 2 つのシステムの使用方法を学ぶこともお勧めします。
分数を簡略化する
既約分数の場合は、最大の数で構成される分数をできるだけ減らすという別の方法を使用できます。この還元を行う際に、小さい方の部分がもう一方の既約であることが判明した場合、それらは等しいと仮定できます。
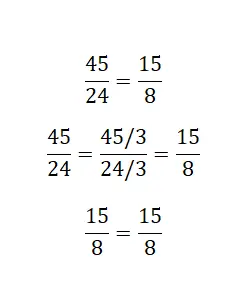
分割を解決して均等化する
最後に、帯分数は常に除算であるため、分数によって生成される商の解を利用することができます。基本的に、2 つの分数の等しい数値を計算する必要があり、それが同じ数値であれば、それらは等価になります。次の画像では、非常に明確な例が見られます。
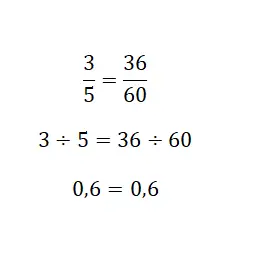
相当する分数の練習
理論全体を読んだので、次の演習を解いてみて、説明を理解することができます。ご自身で解決してみて、解決できたら、その結果と当社が提供する結果を比較することをお勧めします。つまり、次のことを練習してもらいます。
演習 1
私たちが提供する各分数を単純化して同等の分数を見つけます。
この演習を解くには、分数の単純化を適用するだけで、同等の既約分数が得られます。 4 つの例は非常に似ているため、解くのはそれほど難しくありません。
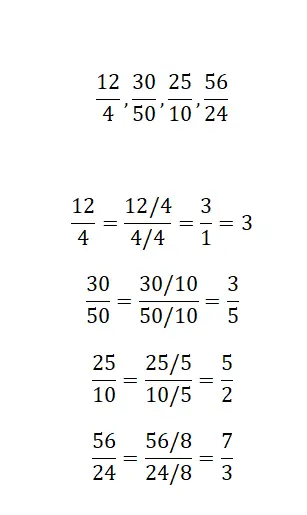
演習 2
私たちが提案する各分数の増幅によって等価な分数を見つけます。
次に、提案する分数を増幅する必要があります。これにより、より大きな等価分数が得られます。掛け算にどのような数値を使用するかは関係ありません。たとえば、2 と 3 を使用します。
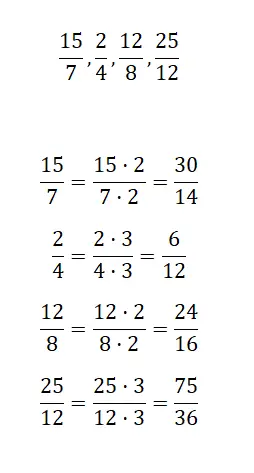
演習 3
次の分数が等しいかどうかを判断します。
2 つの分数が等しいかどうかを確認するには、上で説明した 3 つの方法のいずれかを使用する必要があります。最初の手順で修正が解決されることがわかりますが、どのシステムを使用するかは自由です。
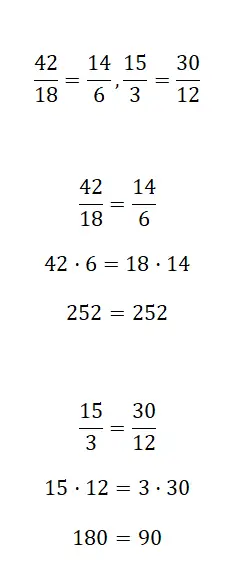
演習 4
次の式の等価な分数を計算します。
この最後の演習では、等価関係を維持するために、提案する式 (整数と帯分数) を分数形式で書き直す必要があります。