分数の簡略化または分数の縮約は、複素分数を別のより単純な同等の分数に変換することを目的とした数学的手順です。したがって、これにより元の式の既約分数を見つけることができ、これはいくつかの方法で実行できます。ただし、説明する前に、このテキストのすぐ下にある分数の簡略化計算を試してみることをお勧めします。
オンライン分数簡略化
オンラインで分数を簡略化する次の計算機を使用すると、あらゆる種類の帯分数を約分できます。分子と分母の値を入力し、単純化ボタンをクリックするだけです。これを実行すると、最も単純化された式が得られます。
分数を簡略化するにはどうすればよいですか?
前に述べたように、分数の単純化には、より複雑な分数の既約分数を見つけることが含まれます。現在、分数を単純化する方法は 2 つあります。1 つ目は通常の除算を使用する方法で、2 つ目は共通因数を抽出する方法です。
割り算による分数の簡略化
この系は、分子と分母の両方を公約数 (1 を除く) で、公約数がなくなるまで割り算することで構成されます。こうすると、既約分数が得られます。各割り算で使用する約数を選択するには、2 つの異なる方法があります。1つ目は、その分数の最も単純な形が得られるまで公約数を使用すること、2 つ目は、次の最大公約数を計算することです。分子と分母。
たとえば、分数 12/64 を簡略化したい場合は、分子と分母を両方の gcf で割るか、既約分数が得られるまで分数の両方の部分を同じ数で割ることによって行うことができます。最小の約数 (1 は数えません) から順に増加します。以下に、両方の方法を段階的に解決した様子を示します。
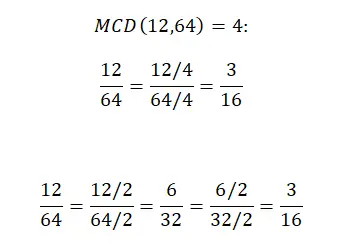
共通因数抽出による分数の簡略化
この別の方法を実行するには、分子と分母を素数に分解する必要があります。そして、等価べき乗の積を元の数値に置き換えます。次に、べき乗の性質を利用して、共通の基底でべき乗を簡略化し、表現を削減していきます。次に、この方法を使用して分数の例を単純化します。
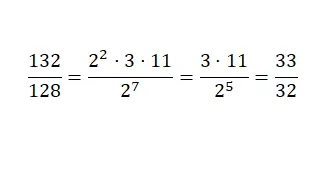
減らすのが難しい分数
次に、最も複雑な単純化のケースに関するいくつかの疑問を解決します。これにより、提案された端数を減らすことができます。このセクションはオプションですが、練習を始めたい場合は、最後のセクションまでスキップしてください。
指数を使って分数を簡略化する
このタイプの分数を単純化するには、指数式を単一の数値として記述する必要があります。まず、素因数分解を試して、分子と分母を単純化します。そして、まだ約分できない分数が得られていない場合は、約分できない式が得られるまで分数の 2 つの部分を分割します。ご覧のとおり、分数をべき乗で単純化するには、前のセクションで説明したすべての方法を組み合わせる必要があります。
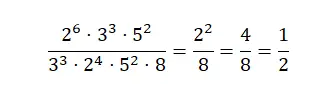
負の分数を単純化する
負の分数を簡略化したい場合、符号は計算手順に直接影響しないため、前に説明した 3 つの方法のいずれかを使用して簡略化できます。結果に必要な変更は 1 つだけで、それは負符号を追加することです。ただし、その他はすべてまったく同じです。それがわかるように、解決済みとして説明した最初の例を以下に示しますが、マイナス記号が付けられています。
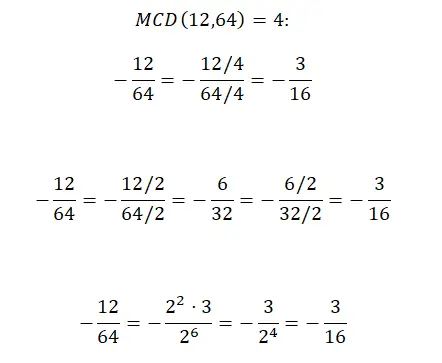
大きな数値を含む分数の簡略化
この場合、大きな数を素因数で表現すると扱いやすくなるため、共通因数抽出法を使用することをお勧めします。したがって、既約分数に到達するまで多くの割り算を解く必要がなくなります。ただし、実際には好きな方法を使用できます。
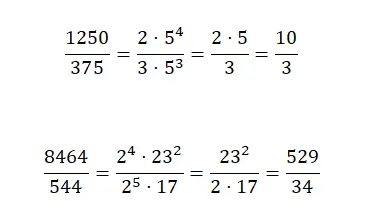
関数電卓で分数を簡略化するにはどうすればよいですか?
多くの関数電卓では、既約でない限り、必要な分数をより簡単な方法で表現できます。カシオの関数電卓(学生に最も多く使われているブランド)の場合は、「S⇔D」と書かれたボタンを押す必要があります。このおかげで、分数を含むすべてのタイプの式を簡略化できるようになります。他のブランドにもこれを行う方法がありますが、従う手順が若干異なる場合があるため、モデルのマニュアルを参照する必要があります。

分数を簡略化するための解決済み演習
ここでは、分数を簡略化するための演習をいくつか紹介します。これを使用して、これまで説明したさまざまな方法を練習できます。理論的な部分を実践と同じくらい重要視して取り組むことをお勧めします。理論的な部分のおかげで、このタイプの演習に含まれる数学的概念を完全に理解できるからです。
演習 1
既約分数が見つかるまで、次の分数を単純化します。
次の画像では、3 つの方法のいずれかを使用して簡略化された 4 つの分数が示されています。自分でこれらを削減しようとする場合は、好みの方法で行うことができますが、重要なのは正しい結果が得られることです。その結果を、修正で示した結果と比較する必要があります。

演習 2
次の分数方程式の x の値を計算します。
ここで、分数を含む 2 つの方程式を提供します。これらは単純化によって解くことができます。これは少し複雑な演習ですが、この記事で説明したいくつかの基本的な数学的概念を適用することで、簡単に解くことができるようになります。
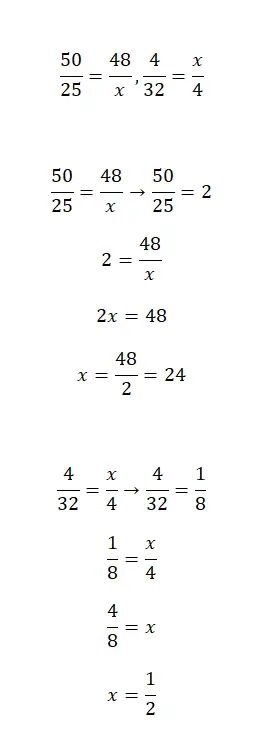
演習 3
以下に示す各分数の等価既約分数を計算します。
ここで、これらの分数をできるだけ単純化することに挑戦します。問題を解くと、前の分数よりも少し難しいことがわかります。 1 つは負の符号を含み、もう 1 つは大きな数値を含み、もう 1 つは累乗を含むためです。

分数に関するさらに演習が必要な場合は、この最後のリンクにアクセスすることをお勧めします。そこでは、分数に関する多くの問題と演算が見つかります。これを使用すると、分数に関連するすべての概念を練習できます。