分数または帯分数は、ある量を別の量で割ることを示す数値表現です。したがって、これは 2 つの数値の商によって表される値です。このタイプの数値を使用すると、小数および整数の数量を表すことができ、比率を示すこともできます。次に、分数をより数学的な方法で定義し、この概念を図で理解できるようにいくつかの例を示します。
分数とは何ですか?
分数は、単位を等しい部分に分割したときの部分の数に等しくなります。したがって、図的には、中央の水平線で区切られた 2 つの項で表されます。より正確には、行の一番上に分子があり、分母の下にあります。
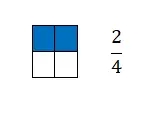
ご覧のとおり、分数は比率と密接に関連しているため、グラフを作成するのが非常に簡単な数学の概念です。前の例で色付きの正方形の数を分数で表現したのはこのためです。
分数項
分数の 2 つの部分は次のとおりです。
- 分子:この用語は水平線の上にあり、ここに取得するピースの数を書き込みます。正、負、ゼロ (ゼロに等しい) の分子を見つけることができます。
- 分母:このもう 1 つの項は線の下にあり、ここにユニットが分割される部分の合計数を書き込みます。正の分母と負の分母を見つけることはできますが、これらをゼロにすることはできません。
分数の種類
分数には、それを構成する数値や他の分数との等価性に応じて、多くの種類があります。次に、存在するすべてのカテゴリを定義し、それらを他のカテゴリと区別できるようにする特性についてコメントします。
- 固有分数:分母よりも小さい分子によって形成される分数です。これらの分数を 10進数に変換すると、0 から 1 までの数値が得られます。分子の値は常に分母の値より小さく、したがって 1 を超えることはないため、1 より大きくすることはできません。
- 仮分数:分子が分母より大きいもので、この場合は 1 より大きい数値を表します。たとえば、8/5 は 1.6 に等しく、1 より大きいです。 これらは帯分数を表す別の方法であり、次のタイプがあります。
- 帯分数:帯分数とも呼ばれ、整数と帯分数で構成されるものです。基本的には分数の前の整数値で表されるため、不正な分数に変換するには、整数部分に分母を掛けて分子に加え、分母はそのままにする必要があります。
- 小数分数: 10 のべき乗に相当する数量を表す分母を持つ分数です (例: 6/10、34/1000、または 5/100)。これらは10 進表記で使用され、正確な 10 進数を帯分数に変換する場合に最も一般的です。これについては次のセクションで詳しく説明します。
- 複分数:分子、分母、またはその両方が別の分数で構成されている分数です。したがって、これらの式を単純化して単一の分数として示すには、分子を分母で割る必要があります。これは、分数の割り算を説明するとより明確になります。
- 等価分数:同じ分子または分母で構成されていないにもかかわらず、同じ数に等しい分数です。たとえば、8/4 = 4/2 = 2、どちらの分数も 2 に等しくなります。この特定のケースでは、最初の分数が 2 番目の分数の 2 倍に等しいため、比例関係が維持されます。
- 既約分数:分子と分母に共通の因数がないため、これ以上単純化できない分数であり、したがってどのような数でも割ることができません。このタイプの例としては、9/5、5/6、7/8 などがあります。それらを検出する方法を知るには、最大公約数の計算方法を知ることが重要です。
分数を使った演算
存在する分数のさまざまなカテゴリがわかったので、次は帯分数を使用したさまざまな算術演算を解く方法を見ていきます。これは整数の演算よりも少し複雑ですが、方法論を理解すれば、すべては非常に簡単であることに注意してください。さらに、理論を説明するだけでなく、いくつかの例も示します。それでは始めましょう。
分数の合計
共通の分母を持つ分数の加算は、2 つの分子を加算し、分母を同じままにするだけなので、非常に簡単です。一方、分母の異なる分数を加算する場合は、分母の最小公倍数を見つける必要があるため、少し難しくなります。次に、lcm (新しい分母) を古い分母で割って、各分子の積を加算する必要があります。より深く理解するには、次の図を見てください。
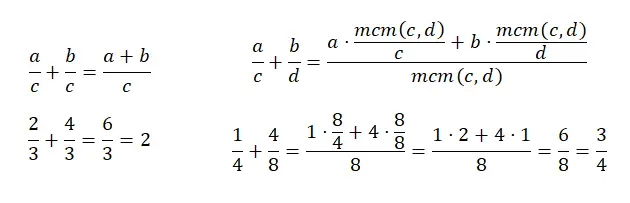
引き算の分数
共通の分母を持つ分数の減算は加算に非常によく似ています。実際、加算の代わりに減算する必要があるため、分子の合計を除いてすべてが同じ方法で行われます。そして、異なる分母を持つ分数の引き算でも同じことが起こります。 lcm を古い分母で割って分子の積を加算する代わりに、 を減算しなければならないことを除けば、実質的に同じことです。これは別の図です。
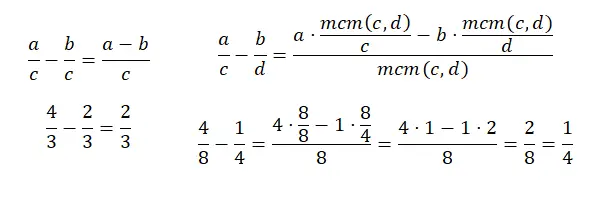
分数の掛け算
分数のかけ算は、分母が同じかどうかに関係なく、同じ方法で解くことができます。基本的に、分子にある部分を掛け、分母に別の部分を掛ける必要があります。これは、2 つの乗算を実行するだけなので、おそらく最も単純な演算です。
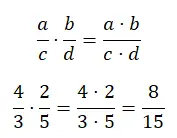
分数の割り算
分数の割り算も非常に簡単に解けます。クロスを掛けるだけです。言い換えれば、分子は最初の分数の分子と 2 番目の分数の分母を乗算した結果です。一方、分母は最初の分数の分母と 2 番目の分数の分子の積です。
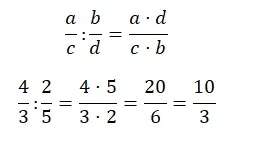
分数を簡略化する
分数の簡略化または分数の約分は、それ自体は算術演算ではありませんが、その方法を知ることは非常に重要です。また、分数の種類についてはすでに少し説明したトピックでもあります。したがって、帯分数を単純化するには、分子と分母を同じ数で割る必要があります。一般に、この単純化を行うために最大公約数を選択します。次の画像に例があります。
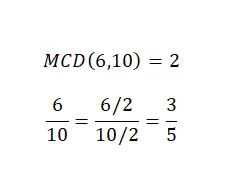
ご覧のとおり、同等の分数が2 つあり、どちらも同じ数値を表しますが、2 番目の分数は最初のものより単純です。したがって、簡素化の目標は達成できました。
小数から分数へ、またはその逆にするにはどうすればよいですか?
生成分数は、 10 進数 (正確な 10 進数または繰り返し 10 進数) から得られる既約分数です。もちろん、小数の種類に応じて異なる方法を使用する必要がありますが、これについては後で説明します。
正確な小数から生成分数への変換
この場合、最初に説明した小数を利用できます。単純に、分子に数値を書き込む必要がありますが、小数点は付けません。分母には、分子の桁数と同じ数のゼロを含む 10 のべき乗を書きます。
ただし、4.25 など、1 より大きい 10 進数がある場合は、完全なユニットの数に分母の値を掛けて、元の分子に加算する必要があります。以下に各タイプの例を示します。
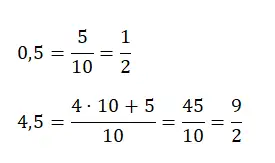
純粋な繰り返し小数を生成分数に変換します
純粋な周期 10 進数がある場合、生成する分数を取得したい場合は、分子に同じ値を入力しますが、小数点は付けず、整数部分を減算する必要があります。分母は 9 だけで構成される数値に等しくなりますが、元の数値の小数部分の桁数と同じ数の 9 を具体的に記述する必要があります。このシステムはややわかりにくいですが、いくつかの例を見て理解してみましょう。
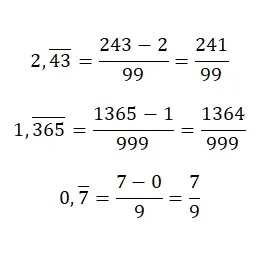
混合繰返し小数を分数生成に変換する
混合繰り返し 10 進数がある場合、かなり複雑なルールを適用する必要があります。まず、分子にカンマなしの数値を書き、整数部分と、その後に続く非繰り返し小数を、これもカンマなしで引きます。分母については、周期小数部分の桁数と同じ数の 9 を書き、その後非循環小数部分の桁数と同じ数のゼロを書く必要があります。
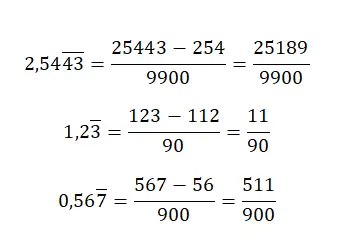
分数を小数に変換する
分数から小数に変換するには、分子を分母で割るだけです。帯分数は2 つの値の商にすぎないからです。したがって、割り算を解くと、対応する 10 進数が得られます。次の画像には、非常に単純な例がいくつかあります。
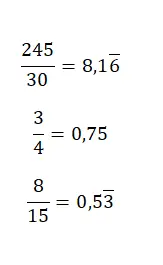
分数の練習
分数に関する理論はすべて理解できたので、いくつかの演習を行うことをお勧めします。こうすることで、説明されているすべての概念をより深く学ぶことができ、試験当日には計算をより速く解くことができます。さらに、存在するすべての種類の分数の練習問題を確認し、それに応じて解く方法もわかります。最後に、すべての分数演算を解決できるオンライン分数計算機もご用意していることをお知らせします。