このページでは、3 つのベクトルの混合積 (または三重点積) とは何か、およびその計算方法を説明します。また、このタイプのベクトル間の演算に関する例、演習、および解決された問題も表示されます。さらに、混合製品の特性と用途もわかります。
3 つのベクトルの混合積は何ですか?
3 つのベクトルの混合積(トリプル ドット積とも呼ばれます) は、 ドット積とベクトル積という 2 つの異なるタイプの演算を含む 3 つのベクトル間の連続乗算です。したがって、2 つのベクトル演算を組み合わせるとスカラー (実数) が得られます。
具体的には、混合積は 2 つのベクトルのベクトル積を計算し、その後、得られた結果に 3 番目のベクトルをベクトル乗算することで構成されます。このように書くと非常に複雑に見えるかもしれませんが、実際にはそれほど複雑ではありません。三重点積の式を見てください。
![]()
その式から分かるように、3 つのベクトルの混合積は 2 つの角括弧で示されます。
3 つのベクトルの混合積を計算するにはどうすればよいですか?
三重ドット積の公式は前のセクションで説明したものですが、より簡単で高速な別の方法があるため、一般的には 3 つのベクトルの混合積を求めるためには使用されません。
任意の 3 つのベクトルを次のようにします。
![]()
3 つのベクトル間の混合積を計算するには、ベクトルの成分によって形成される 3×3 行列式を解くだけです。
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a3fed933d4d02bb5ca6f5bae06ea544d_l3.png)
これがどのように計算されるかの例を見ることができます。次の 3 つのベクトルの混合積が求められます。
![]()
混合積を決定するには、行列の行にベクトルを配置して次数 3 の行列式を構築します。
![Rendered by QuickLaTeX.com \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e5341b4a39b42c1284a4b0129b38b61a_l3.png)
ここで、行列の行列式を解く必要があるだけです。これには任意の方法を使用できます。この場合、Sarrus の法則を適用します (ただし、これは加算または余因子によっても実行できます)。
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-df86565048cf897265878936f2294525_l3.png)
2 つの手順が同等であることを示すために、次の定義に従って同じベクトルの混合積を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e4d15d610ca9b4cb39e9f268cfb152ae_l3.png)
ベクトルの行列式を使用して混合積を計算することをお勧めします。これは、高速で間違いを犯す可能性が低いためです。ただし、ご覧のとおり、どちらの方法を使用しても結果は同じなので、お好みの方法を使用してください。 👍
混合積の幾何学的解釈
3 つのベクトルの混合積を求める方法がわかると、混合積は何のためにあるのか疑問に思うかもしれません。数学では、平行六面体の体積と四面体の体積を計算するという 2 つの主な用途があります。
平行六面体の体積は、幾何学的フィールドの 3 次元をマークするベクトルの混合積の絶対値に等しくなります。
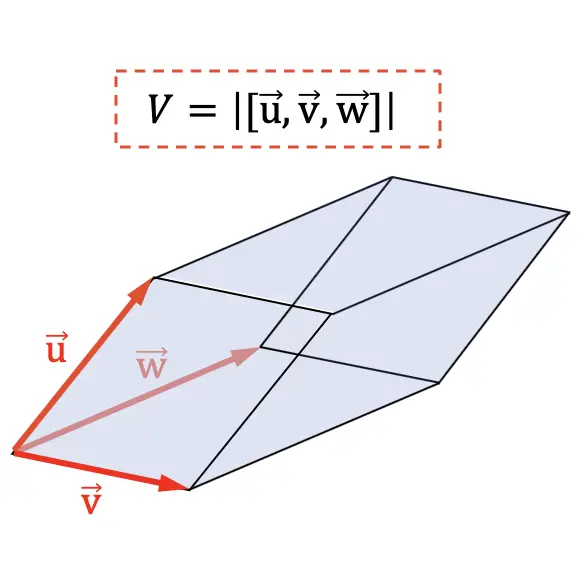
混合積の別の用途は、四面体の体積を決定することです。幾何学的には、混合積の絶対値の 6 番目の部分は四面体の体積を表すため、次のようになります。
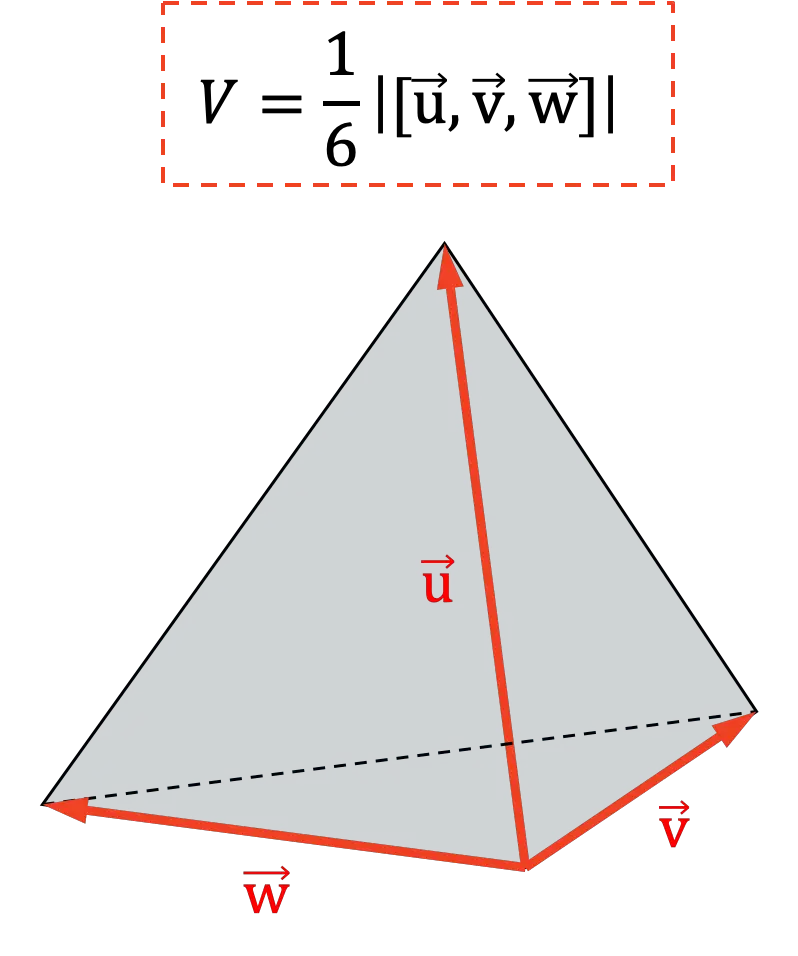
混合積またはトリプルドット積の特性
混合積、つまりトリプル スカラー積には、次の特性があります。
- 一般に、混合積ベクトルの順序の変化は、符号の変化も意味します。したがって、混合積ベクトルの順序が重要です。
![]()
- ただし、順序を周期的に変更しても、符号は変わりません。
![]()
- 3 次元空間 (R3 内) では、(同じ平面に属する) 3 つの線形依存ベクトルまたは共面ベクトルの混合積は 0 に等しくなります。
混合製品の問題を修正
演習 1
3 つのベクトルが与えられた場合:
![]()
3 つのベクトルの混合積を計算します。
![]()
その混合積を見つけるには、ベクトルの座標で構成される行列式を解く必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-549ed90889d541ae4a1075449567b062_l3.png)
演習 2
3 つのベクトルが与えられた場合:
![]()
3 つのベクトル間の混合積を決定します。
![]()
その混合積を見つけるには、線形のベクトルのデカルト座標を持つ行列式を解く必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29b46155243552a99f6fd75de69f59da_l3.png)
演習 3
3 辺が次のベクトルである直方体の体積を計算します。
![]()
直方体の体積は、辺として持つ 3 つのベクトルの混合積の絶対値に等しくなります。したがって、最初にベクトルの三重外積を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9718b369a508216fbb69ab68ac7de381_l3.png)
したがって、直方体の体積は混合積の結果の絶対値になります。
![]()
演習 4
次の点を頂点とする四面体の体積を計算します。
![]()
まず、四面体のエッジを表すベクトルを計算します。
![]()
![]()
![]()
四面体の体積は、四面体のエッジに対して持つ 3 つのベクトルの混合積の絶対値の 1/6 に相当します。したがって、最初に、見つかったベクトルの混合積を計算します。
![Rendered by QuickLaTeX.com \begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d384e76415a756b834e0a8e7c695b1c1_l3.png)
したがって、四面体の体積は、混合積の絶対値の 6 分の 1 になります。
![]()