行列の乗算 - Mathority

このページでは、2×2、3×3、4×4などの次元の行列を乗算する方法を見ていきます。行列の乗算の手順を例を使って段階的に説明し、解決済みの練習問題も用意されているので、練習することもできます。最後に、2 つの行列を乗算できない場合と、この行列演算のすべてのプロパティを学習します。

2 つの行列を乗算するにはどうすればよいですか?

例を使用して 2 つの行列の乗算を実行する手順を見てみましょう。

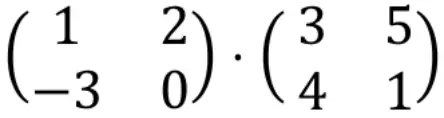
行列の乗算を計算するには、左側の行列の行を右側の行列の列で乗算する必要があります。

したがって、最初に最初の行と最初の列を乗算する必要があります。これを行うには、最初の行の各要素と最初の列の各要素を 1 つずつ乗算し、結果を加算します。したがって、これらすべてが結果の配列の最初の行の最初の要素になります。手順を見てください。

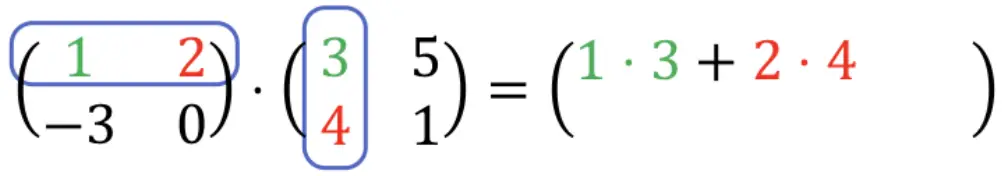
1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11。つまり、次のようになります。

次に、最初の行と 2 番目の列を乗算する必要があります。したがって、この手順を繰り返します。最初の行の各要素と 2 番目の列の各要素を 1 つずつ乗算し、その結果を加算します。これらはすべて、結果の配列の最初の行の 2 番目の要素になります。

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7。つまり、次のようになります。

結果の行列の最初の行を埋めたら、2 番目の行に移動します。したがって、次の手順を繰り返して、2 行目と1 列目を乗算します。2 行目の各要素と 1 列目の各要素を 1 つずつ乗算し、その結果を加算します。

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9。まだ：

最後に、 2 番目の行と 2 番目の列を乗算します。常に同じ手順で、2 行目の各要素と 2 列目の各要素を 1 つずつ乗算し、その結果を加算します。

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15。まだ：

そしてここで 2 つの行列の乗算が終了します。これまで見てきたように、行と列を乗算する必要があります。常に同じ手順を繰り返す必要があります。行の各要素と列の各要素を 1 つずつ乗算し、その結果を加算します。

行列乗算の演習を解決しました

演習 1

次の行列積を解きます。

解決策を参照

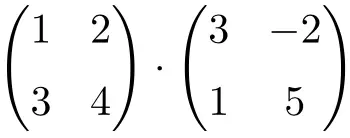
これは次数 2 の行列の積です。

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

行列の積を解くには、左の行列の行と右の行列の列を乗算する必要があります。

したがって、最初に最初の行と最初の列を乗算します。これを行うには、最初の行の各要素と最初の列の各要素を 1 つずつ乗算し、結果を加算します。これらはすべて、結果の配列の最初の行の最初の要素になります。

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

次に、最初の行と 2 番目の列を乗算して、結果の行列の最初の行の 2 番目の要素を取得しましょう。

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

2 行目に移動するので、 2 行目に最初の列を乗算します。

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

最後に、 2 番目の行と 2 番目の列を乗算して、テーブルの最後の要素を計算します。

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

したがって、行列乗算の結果は次のようになります。

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

演習 2

次の 2×2 正方行列の乗算の結果を求めます。

解決策を参照

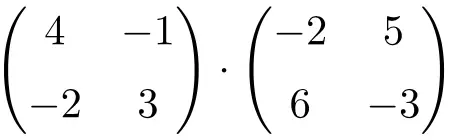
これは 2×2 次元の行列の積です。

乗算を解くには、左の行列の行と右の行列の列を乗算する必要があります。

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

演習 3

次の 3×3 行列の乗算を計算します。

解決策を参照

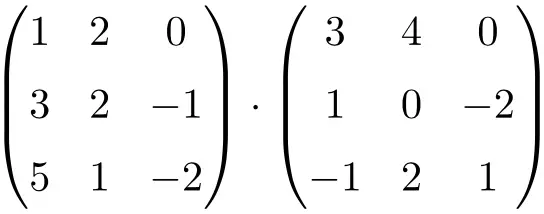
3×3 行列の乗算を実行するには、左の行列の行と右の行列の列を乗算する必要があります。

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

演習 4

行列が与えられると

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

計算します:

$\displaystyle 2A\cdot A^t$

解決策を参照

まず、次の転置行列を計算します。

$A$

乗算を行うために。転置行列を作成するには、行を列に変更する必要があります。つまり、行列の 1 行目は行列の 1 列目になり、行列の 2 行目は行列の 2 列目になります。まだ：

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

したがって、行列演算はそのまま残ります。

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

これで計算ができるようになりました。まず計算します

$2A$

(ただし、最初に計算することもできます

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

そして最後に、行列の積を解きます。

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

演習 5

次の行列を考えてみましょう。

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

計算します:

$\displaystyle A\cdot B - B \cdot A$

解決策を参照

これは、減算と次数 2 の行列乗算を組み合わせた演算です。

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

まず左側の乗算を計算します。

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

ここで、右側の乗算を解きます。

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

そして最後に行列を減算します。

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

2 つの行列を乗算できないのはどのような場合ですか?

すべての行列を乗算できるわけではありません。 2 つの行列を乗算するには、最初の行列の列数が 2 番目の行列の行数と一致する必要があります。

たとえば、最初の行列には 3 列があり、2 番目の行列には 2 行があるため、次の乗算は実行できません。

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

しかし、順序を逆にすると、それらを乗算することができます。最初の行列には 2 つの列があり、2 番目の行列には 2 つの行があるため、次のようになります。

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

行列乗算のプロパティ

このタイプの行列演算には次の特徴があります。

行列の乗算は結合的です。

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

行列乗算には次のような分配特性もあります。

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

行列の積は可換ではありません。

$\displaystyle A \cdot B \neq B \cdot A$

たとえば、次の行列乗算の結果は次のようになります。

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

しかし、行列の乗算の順序を逆にすると、積の結果は異なります。

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

さらに、行列に単位行列を乗算すると、結果は同じ行列になります。これは乗法恒等性プロパティと呼ばれます。

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

例えば：

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

最後に、すでにご想像のとおり、行列にゼロ行列を乗算すると、行列はゼロ行列に等しくなります。これはゼロの乗法的性質と呼ばれます。

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

例えば：

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

2 つの行列を乗算するにはどうすればよいですか?

行列乗算の演習を解決しました

演習 1

演習 2

演習 3

演習 4

演習 5

2 つの行列を乗算できないのはどのような場合ですか?

行列乗算のプロパティ

コメントする 返信をキャンセル

コメントする返信をキャンセル