このページでは、幾何学における 2 点間の距離を計算する方法 (公式) を説明します。また、例を確認したり、2 点間の距離に関する解決済みの演習を使って練習したりすることもできます。
2点間の距離を求める公式は何ですか?
2 つの点の間の距離は、それらを結ぶ線分の長さに等しくなります。したがって、数学では、2 つの異なる点の間の距離を決定するには、それらの座標間の差の二乗を計算し、その二乗の和の根を求める必要があります。
つまり、デカルト平面上の 2 つの異なる点間の距離を計算するために使用される式は次のとおりです。
2 つの異なる点の座標を考えてみましょう。
![]()
2 点間の距離の公式は次のとおりです。
![]()
この式はベクトルの大きさから得られます。実際、この式で行っていることは、問題の 2 点によって決定されるベクトルの大きさを実際に計算していることです。これについては、 ベクトルの係数とは何かという説明で詳しく読むことができます。
一方、解析幾何学では、ピタゴラスの定理を使用して 2 点間の距離の公式を証明することもできます。
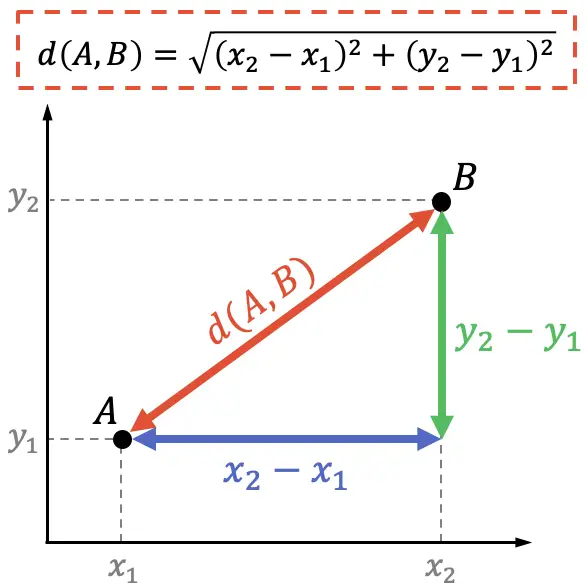
ピタゴラスの定理は、直角三角形の斜辺の二乗はその脚の二乗の和に等しいと述べており、したがって次のようになります。
![]()
式を得るには、2 点間の距離を見つける必要があります。
![]()
最後に、3 座標点を使用している場合、空間 (R3) 内の 2 点間の距離の式は同じになりますが、Z 座標が追加されることは注目に値します。
![]()
2点間の距離の計算例
2 点間の距離の公式の定義を理解したら、例を使用してその距離を決定する方法を見てみましょう。
- 次の 2 点間の距離を求めます。
![]()
2 点間の距離を幾何学的に求めるには、次の式を適用するだけです。
![]()
次に、点の座標を式に代入します。
![]()
そして計算を行います。
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4e48600907e65f89fb9be0d55a2d3b3a_l3.png)
したがって、2 点間の距離は 5 単位に等しくなります。
距離は常に正であるため、距離の値は常に正の符号を示す必要があることは明らかです。そうでない場合は、ステップを間違えたことを意味します。
2 点間の距離のトラブルシューティング
演習 1
次の 2 点間の距離を計算します。
![]()
2 点間の幾何学的距離を求めるには、次の式を使用します。
![]()
次に、点の座標を式に代入します。
![]()
そして計算を行います。
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-81d70676cabdc2985f2ebe7b88c54e2d_l3.png)
演習 2
次の 2 点間の距離を求めます。
![]()
2 点間の数学的距離を求めるには、対応する式を使用する必要があります。
![]()
次に、点の座標を式に代入します。
![]()
そして計算を行います。
![Rendered by QuickLaTeX.com \begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c9f9f5c93377868a352891d5b09630a_l3.png)
演習 3
以下の図に示す点 A、B、C によって形成される三角形の周囲長を計算します。
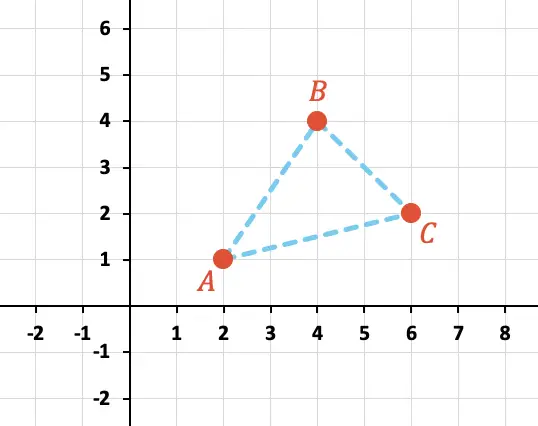
まず、グラフ上の各点の X 座標と Y 座標を特定する必要があります。
![]()
![]()
![]()
次に、次の式を使用してすべての点間の距離を計算する必要があります。
![]()
![]()
![]()
したがって、三角形の周囲の長さは 3 つの辺の長さの合計になります。
![]()
演習 4
点A、B、Cを頂点とする三角形が二等辺三角形であるかどうかを調べます。ただし、次の 3 つのポイントがあります。
![]()
三角形が二等辺であるためには、その辺のうちの 2 つが等しくなければなりません。したがって、頂点間の距離に対応する各辺の長さを見つける必要があります。
したがって、三角形の頂点間の距離を計算します。
![]()
![]()
![]()
したがって、三角形には 2 つの同一の辺があり、3 番目の辺の寸法が他の 2 辺とは異なる場合、実質的には二等辺三角形となります。
演習 5
次の 2 点から等距離にある Y 軸上の点を見つけます。
![]()
まず、点がコンピュータ軸 (OY 軸) 上にある場合、これは点の横座標がゼロであることを意味します。
![]()
次に、点が点 A および B から等距離にある場合、これは次の方程式が満たされていることを意味します。
![]()
したがって、2 点間の距離の公式を使用すると、前の式から変数yの値を見つけることができます。
![]()
方程式の両辺には根があるため、次のように単純化できます。
![]()
注目すべき力と平等(または注目すべき積)を解決します。
![]()
そして、未知のyの値が見つかるまで操作します。
![]()
![]()
![]()
![]()
つまり、問題文が私たちに問いかけている点は次のとおりです。
![]()
この記事が役立つと思われた場合は、点と線の間の距離に関する演習にも興味があるでしょう。リンクされたページには、段階的に解決された演習だけでなく、点と線の間の距離の計算の詳細な説明、別のタイプの距離を決定するための点と線の間の距離の公式の例と応用も含まれています。 。