2 本の線の間の角度 (公式)

このページでは2本の線の間の角度の計算方法（公式）を解説します。また、いくつかの例を見ることができ、さらに、段階的に解決された演習で練習することもできます。

2本の線の間の角度はいくらですか?

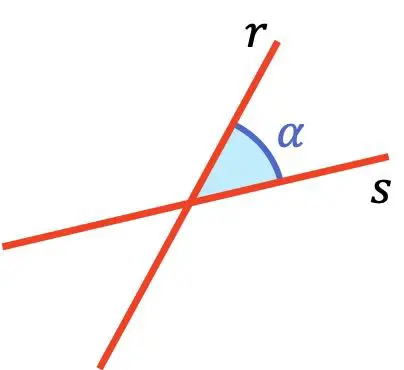
2 本の線の間の角度は、これら 2 本の線の間の最小角度です。

平面図では、線と線とのなす角度に応じて、交差線（0°～90°）、垂直線（90°）、平行線（0°）、一致線（0°）の4種類があります。

交差する線

交差線は 0 度から 90 度までの鋭角で交差します。

垂直直線

垂線は90度の直角で交わります。

平行線

平行線は決して接触せず、その間の角度は 0 度になります。

一致する線

一致する 2 つの直線にはすべての点が共通しているため、それらの間には常に 0 度の角度が存在します。

結論として、2 本の平行線、一致線、または垂直線間の角度の計算はすぐに行われます。平行線と一致線は同じ方向を持っているため、角度 0 度を形成し、垂直線は 90 度の角度で交差します。。一方、交差する 2 つの線の間の角度を求めるには、公式を適用する必要があります (これについては以下で説明します)。

2 本の線の間の角度はどのように計算されますか?

2 本の線の間の角度を計算するには 2 つの方法があります。最初の方法は各ラインの方向ベクトルを使用し、2 番目の方法は各ラインの傾きに基づきます。

どちらの手順が優れているというわけではなく、実際にはどちらも非常に簡単ですが、線の表現方法に応じてどちらかの方法が実用的になります。したがって、両方の数学的手法の使用方法を理解しておくことをお勧めします。

線ベクトル配向法

方向ベクトルを使用して 2 つの線の間の角度を計算する式は次のとおりです。

2 つの異なるラインの方向ベクトルを考えると、次のようになります。

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

これら 2 本の線の間の角度は、次の式で計算できます。

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

金

$\lvert \vv{\text{u}} \rvert$

そして

$\lvert \vv{\text{v}} \rvert$

ベクトルのモジュールです

$\vv{\text{u}}$

そして

$\vv{\text{v}}$

それぞれ。

ベクトルの大きさの公式は次のとおりであることに注意してください。

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

例を使用して 2 つの線の間の角度を見つける方法を見てみましょう。

次の 2 つの線の間の角度を計算します。

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

2 本の線の間の角度を計算するには、まず各線の方向ベクトルを見つける必要があります。

権利

$r$

はパラメトリック方程式の形式で表現されるため、その方向を示すベクトルの成分は次のようになります。

$\vv{r} = (-3,4)$

そして法律

$\displaystyle s$

は暗黙的な (または一般的な) 方程式の形式で定義されるため、その方向ベクトルの座標は次のようになります。

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

各線の方向ベクトルがわかったので、2 本の線の間の角度の公式を使用できます。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

したがって、2 つのベクトルの大きさを決定します。

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

角度の公式のベクトル演算を実行します。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

そして最後に、コサインの逆数を使用して 2 つの直線によって形成される角度を計算します。

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

キーを使用して電卓を使用すると、コサインの逆数を計算できることを覚えておいてください。

$\boxed{\cos ^{-1}}.$

スロープ法

明らかに、この方法を理解するには、線の傾きを知る必要があります。この概念はリンクで確認できます。この概念の意味、計算方法、例、および線の傾きの演習問題の詳細な説明が記載されています。

2 本の線の傾きから間の角度を計算する式は次のとおりです。

または 2 つの異なる行:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

これら 2 本の線の間の角度は、次の式で求めることができます。

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

金

$m_1$

そして

$m_2$

線の傾きです

$r_1$

そして

$r_2$

それぞれ。

例を使用して、傾きを使用して 2 つの線の間の角度を計算する方法を見てみましょう。

次の 2 つの線の間の角度を求めます。

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

各線の傾きは変数の前の数値です。

$x:$

$m_r = 4$

$m_s = -3$

したがって、2 つの線の間の角度は、次の傾き公式を適用することで求めることができます。

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

そして最後に、接線の逆角度を求めます。

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

キーを使用して電卓を使用すると、正接の逆数を計算できることを覚えておいてください。

$\boxed{\tan ^{-1}}.$

2 つの直線の傾きを明示的な方程式として表現した例を先ほど見ましたが、それらが点傾き方程式の形式である場合は、これと同じ手順を使用する必要があります。

2 本の線の間の角度の問題を解く

演習 1

次の 2 つの直線によって形成される角度を決定します。

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

解決策を参照

この場合、方向ベクトル法を使用します。したがって、最初に各ラインの方向ベクトルを見つける必要があります。どちらの直線もパラメトリック方程式として表現されるため、方向ベクトルの成分はパラメーターの前の項になります。

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

各線の方向ベクトルがわかったので、2 本の線の間の角度の公式を使用できます。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

したがって、2 つのベクトルの大きさを決定します。

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

分子の 2 つのベクトル間のスカラー積と、分母のモジュールの乗算を解きます。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

そして最後に、コサインの逆関数を実行して、2 つの線によって形成される角度を見つけます。

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

演習 2

次の 2 つの線の間の角度を求めます。

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

解決策を参照

この問題を方向ベクトル法を使って解くので、まず各ラインの方向ベクトルを求める必要があります。権利

$r$

は、その方向を示すベクトルの成分が次のような一般 (または暗黙的な) 方程式の形式で表現されます。

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

そして法律

$\displaystyle s$

は連続方程式の形式で定義されるため、その方向ベクトルのデカルト座標は分母の数になります。

$\vv{s} = (6,3)$

各線の方向ベクトルがわかったら、2 本の線の間の角度の公式を使用できます。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

したがって、2 つのベクトルのモジュールを決定します。

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

角度の公式のベクトル間の演算を実行します。

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$