このページでは、2 つのベクトルの外積とは何か、およびその計算方法について説明します。また、右手の法則 (またはコルク栓抜き) を使用して、外積の方向と方向を求める方法も説明します。さらに、このタイプの操作の使用法だけでなく、例、演習、問題が段階的に解決されることもわかります。
2 つのベクトルの外積は何ですか?
数学では、外積は3 次元空間 (R3) 内の 2 つのベクトル間の演算です。このベクトル演算の結果は、乗算された 2 つのベクトルに垂直な方向を持ち、モジュールが乗算ベクトルのモジュールとそれらが形成する角度の正弦の積に等しいベクトルになります。つまり、その式は次のようになります。
![]()
前の式でわかるように、外積は次のように表されます。
![]()
、そのため、外積とも呼ばれます。彼が発明したため、ギブス ベクトル積と呼ばれることもあります。
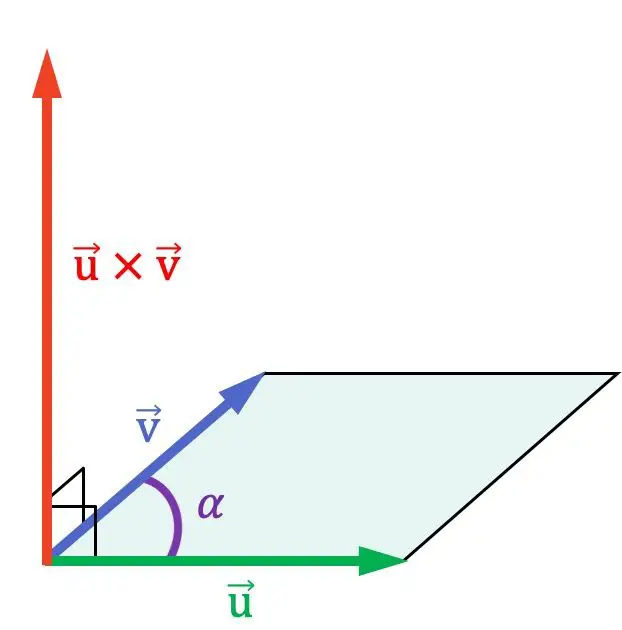
前のグラフ表示でわかるように、外積は乗算される 2 つのベクトルに対して垂直であるため、それらを含む平面に対して垂直になります。
2 つのベクトルの外積を計算する式
ベクトルのデカルト座標がわかっている場合、その外積を計算する最も簡単な方法は、3×3 の行列式を解くことです。それがどのように行われるかを見てください:
任意の 2 つのベクトルを考えてみましょう。
![]()
そのベクトル積は次のとおりです。
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-56551111a4f5a18a4609772ebaeaf919_l3.png)
ベクトルがどこにあるか
![]()
これらはそれぞれ X、Y、Z 軸方向の単位ベクトルです。
2 つのベクトル間の外積を計算する方法の例を見てみましょう。
![]()
ベクトル間のベクトル積を決定するには、次の次数 3 の行列式を作成する必要があります。
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-abc77b698bf6f4fddec1ab2dcc8b07f0_l3.png)
この場合、アジュバントまたは補因子によって行列式を解きます (Sarrus ルールも使用できます)。
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eeeac04b3f0edd64e5413629051551fd_l3.png)
したがって、2 つのベクトルのベクトル積の結果は次のようになります。
![]()
外積の方向と方向を決定します
外積から得られるベクトルの成分を知る必要がない場合もありますが、モジュール、その方向、およびその方向を見つけるだけで十分です。これは物理学、特に力の計算でよく起こります。
したがって、ベクトルの積の方向と方向を求めるための規則がいくつかあります。最もよく知られているのは、3 本の指または手全体を使用する右手の法則と、コルク抜きの法則 (またはネジ)です。どれでも使用できるので、すべてを知る必要はありません。引き続き 3 つのルールについて説明しますので、最も気に入ったものを使用してください。 😉
右手の法則(3本指)
右手のルールまたは法則の 3 本指バージョンでは、次の手順を実行する必要があります。
- 右手の人差し指を外積の最初のベクトルに向けて置きます。

- 右手の中指 (または中指) を外積の 2 番目のベクトルに向けて置きます。

- 結果として得られる親指の位置は、外積の方向と方向を示します。

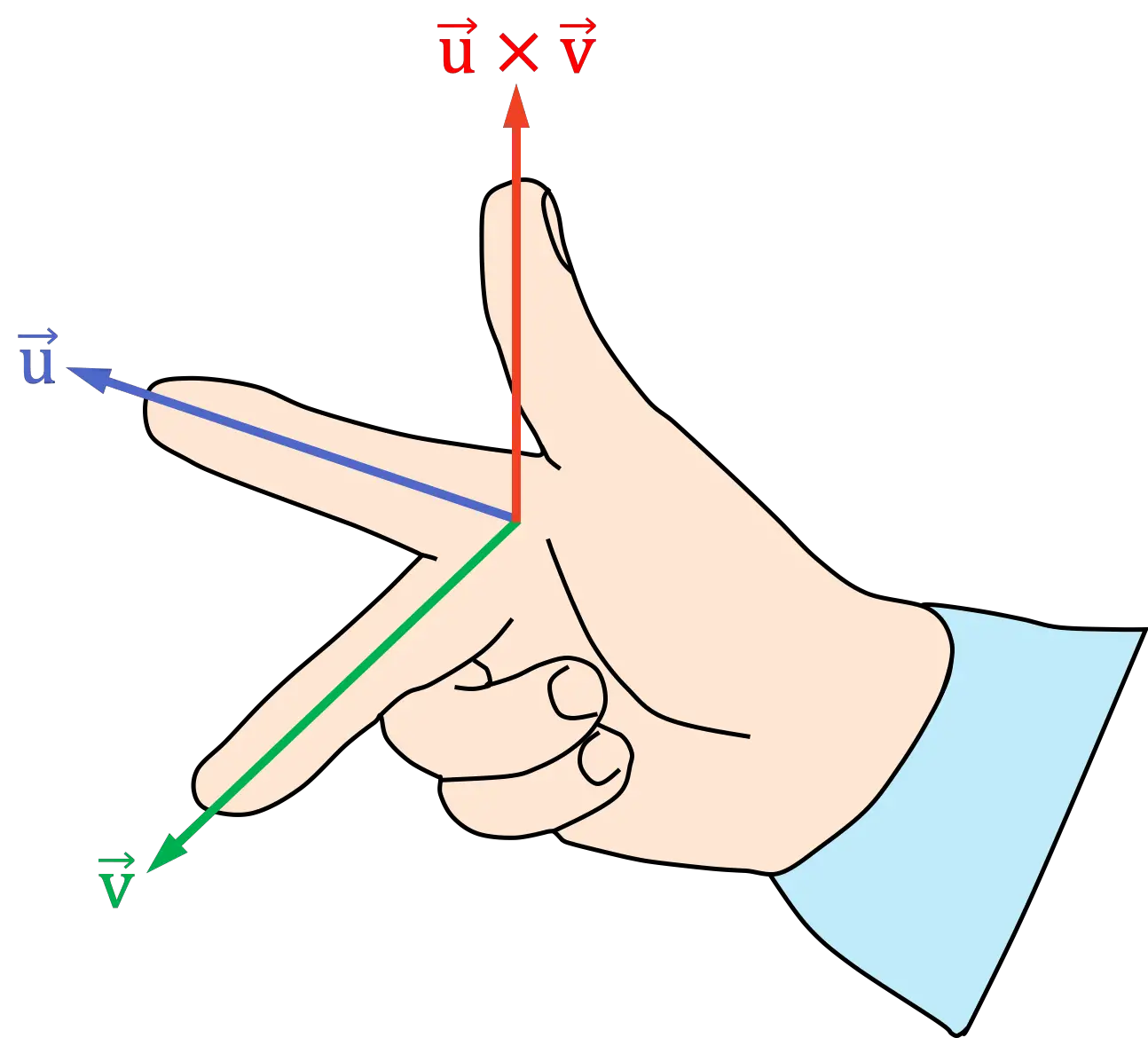
右手の法則(手のひら)
右手の法則または法則の手のひらバージョンは、前のルールと非常によく似ています。これを適用するには、次の手順に従う必要があります。
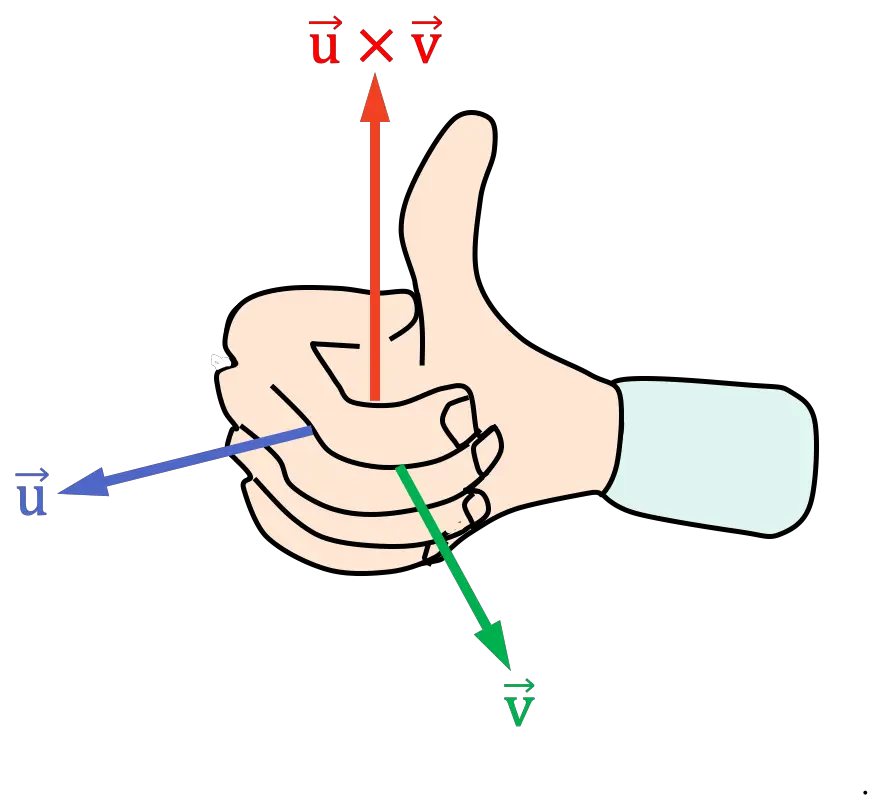
- 右手を指で外積の最初のベクトルと同じ方向に向けます。

- 外積の 2 番目のベクトルに向かって指を動かして右手を閉じます。

ベクトル間の角度(または距離)が小さい側で手を閉じる必要があります。
- 結果として生じる親指の位置によって、外積の方向が決まります。

コルク抜きルール
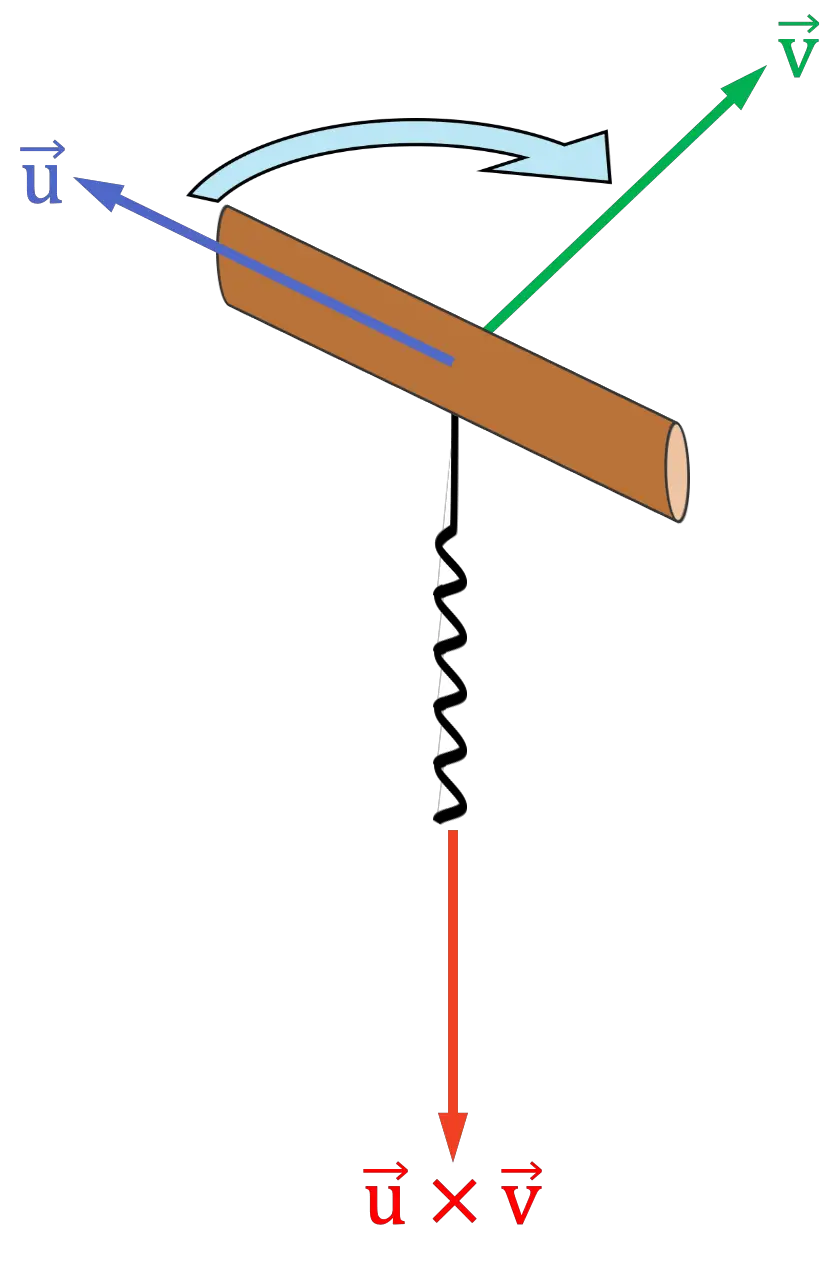
コルク栓抜きまたはねじの法則は、手のひら全体を使用する右手の法則に似ています。手順は次のとおりです。
- 想像力を働かせて、ハンドルが外積の最初のベクトルと同じ方向を向くようにコルク栓抜き (またはネジ) を配置します。

- 次に、コルク抜きを外積の 2 番目のベクトルに向けて回転させます。
まるでコルクに詰めるかのように。ベクトル間の距離が最も短くなる側にコルク抜きを回す必要があります。
- コルク栓抜きの螺旋が指す方向がベクトル積の方向と方向になります。

2 つのベクトルの外積のプロパティ
2 つのベクトルの外積には次の特性があります。
- 反可換性:符号がそれに応じて変化するため、ベクトル積に含まれるベクトルの順序は無関係ではありません。
![]()
- ベクトルの加算と減算に関する分配特性:
![]()
![]()
- 同次特性: 外積のベクトルにスカラー (実数) を乗算することは、外積の結果にそのスカラーを乗算することと同じです。
![]()
- ベクトル積から得られるベクトルは、演算に含まれる 2 つのベクトルに対して垂直です。
![Rendered by QuickLaTeX.com \begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a96345e09a0fdb952557c9138c72ac4_l3.png)
- さらに、2 つのベクトルが直交する場合、次の方程式が満たされます。
![Rendered by QuickLaTeX.com \vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d49d463798c6381c9a8c065417ee3dbf_l3.png)
- 2 つの平行ベクトルの外積は、ゼロ ベクトル (またはゼロ) に等しくなります。
![]()
- 2 つのベクトルによって形成される角度がわからない場合、次の式を使用してそれらのベクトル積の係数を計算することもできます。
![]()
外積を使用して、平行四辺形または三角形の面積を計算します。
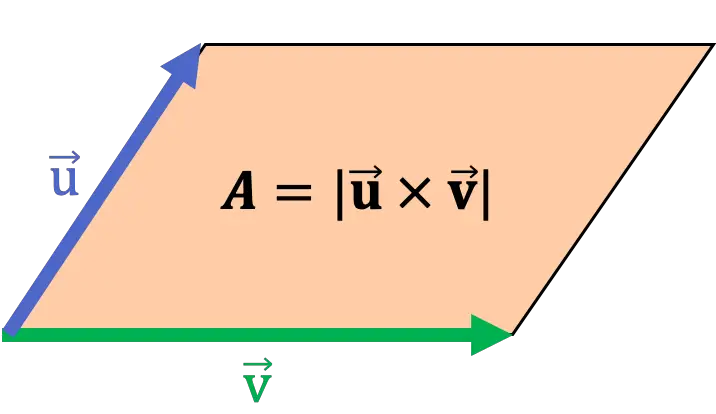
幾何学的には、2 つのベクトルの外積の係数は、これら 2 つのベクトルを辺とする平行四辺形の面積と一致します。したがって、外積を使用して、平行四辺形の面積を計算できます。
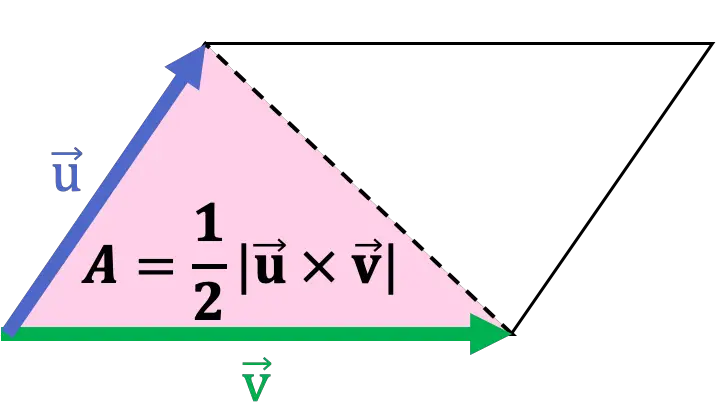
さらに、平行四辺形の対角線はそれを 2 つの三角形に分割します。つまり、三角形は平行四辺形の半分です。したがって、三角形の面積は、 2 つの辺をベクトルとしてとった外積の係数の半分になります。
3 次元空間におけるベクトルの法は、その座標の二乗和の根であることを思い出してください。
![]()
これらは、数学の分野における 2 つのベクトルの外積の 2 つの応用例です。ただし、物理学では磁場の計算に使用されるなど、他の用途もまだあります。
ベクトルのベクトル積に関する演習を解決しました
演習 1
次の 2 つのベクトル間の外積を計算します。
![]()
ベクトル間のベクトル積を決定するには、次の次元 3×3 の行列式を解く必要があります。
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-44db63ee02936f6e5f21891c3e412fb6_l3.png)
この場合、アジュバントまたは補因子によって行列式を解きます (ただし、Sarrus ルールを使用することもできます)。
![Rendered by QuickLaTeX.com \begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fe298c37814c92498e4fd8ade0620951_l3.png)
したがって、2 つのベクトルのベクトル積の結果は次のようになります。
![]()
演習 2
次の 2 つのベクトル間の外積を求めます。
![]()
2 つのベクトル間のベクトル積を求めるには、次の 3×3 行列式を解く必要があります。
![Rendered by QuickLaTeX.com \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6a23d8e45f9065f70c576e6b8db02465_l3.png)
この場合、行列式を随伴因子または余因子によって解きます (ただし、Sarrus の規則は同じ意味で使用できます)。
![Rendered by QuickLaTeX.com \begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-02ffb40666893faa7677234065f3f85f_l3.png)
したがって、2 つのベクトル間のベクトル積の結果は次のようになります。
![]()
演習 3
2 つのベクトルのモジュールとそれらが形成する角度を知る:
![]()
2 つのベクトルの外積の大きさを決定します。
次の式を適用すると、2 つのベクトル間のベクトル積の係数を簡単に計算できます。
![Rendered by QuickLaTeX.com \begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-06dcff41e0dcf31152f0047507056f24_l3.png)
演習 4
スクリーン平面に含まれる次のベクトルから:
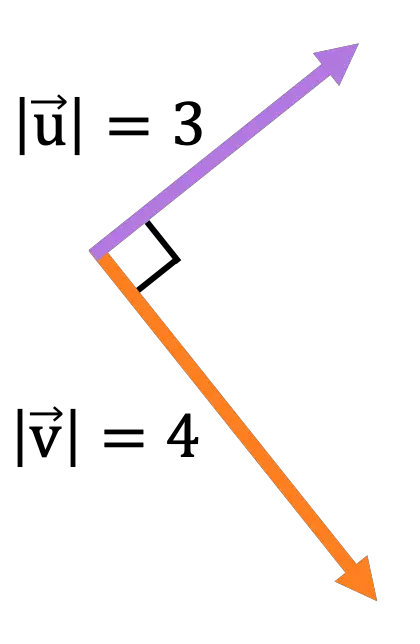
次のベクトル演算の結果として得られるベクトルの大きさ、方向、および意味を計算します。
![]()
2 つのベクトルは垂直であるため、ベクトル積のノルムは次のようになります。
![Rendered by QuickLaTeX.com \begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d8f675fe7eb44c050c508c4771c0a439_l3.png)
一方、ベクトル積から得られるベクトルは、演算に関与する 2 つのベクトルに対して垂直であるため、その方向は画面に対して垂直になります。
そして最後に、直線 (またはコルク栓抜き) ルールを使用して、結果のベクトルの方向が画面の内側に向かうと推定できます。
演習 5
2 つの辺として次のベクトルを持つ平行四辺形の面積を計算します。
![]()
平行四辺形の面積は、それを形成するベクトルの外積の係数と一致します。したがって、ベクトルのベクトル積を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e7c1825be82d94c4eae49c73f509858_l3.png)
そしてモジュールは次のようになります。
![]()
演習 6
次の点を頂点とする三角形の面積を求めます。
![]()
まず最初に、三角形の辺を形成するベクトルを計算する必要があります。
![]()
![]()
三角形の面積は、それを形成するベクトルのベクトル積の大きさの半分です。したがって、ベクトルのベクトル積を計算します。
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-42a0ae5858bcb681ee92ec1ed67424c7_l3.png)
モジュールの後:
![]()
そして最終的に、三角形の面積はモジュールの半分になります。
![]()