このページでは、類似行列とも呼ばれる類似行列について説明します。さらに、疑う余地がないように、2 つの類似した行列の明確な例と、このタイプの行列のすべてのプロパティを示します。最後に、それらが合同行列とどのように関係しているかを確認することもできます。
類似した(または類似した)行列とは何ですか?
類似行列の定義は次のとおりです。
2つの行列
![]()
そして
![]()
行列が存在する場合は類似 (または類似)
![]()
次の条件が満たされます。
![]()
または同等のもの:
![]()
実際、マトリックスは
![]()
基底変化行列として機能します。したがって、この式が意味することは、行列は
![]()
別の基数 (
![]()
)、行列が生じます。
![]()
。
実際に行列を変換しているため、この用語は相似変換とも呼ばれます。
![]()
マトリックスの中で
![]()
。
明らかにマトリックス
![]()
これは、正規行列または非縮退行列 (非ゼロ行列式) でなければなりません。
一方、2 つの行列が次の式に似ていることを示すことができます。
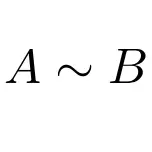
このクラスの行列は、線形代数にとって思っている以上に重要です。行列を対角化する手順は行列の類似性の概念に基づいているため、これらは主に対角化可能な行列に使用されます。
実際、行列を対角化するプロセスには、同時に対角行列である同様の行列を計算することが含まれます。それがどのように行われるかは、 「行列を対角化する方法」で確認できます。
類似または類似の行列の例
次に、2×2 次元の同様の行列の例を見て、概念の理解を完了します。
- 正方行列 A と B は、可逆行列 P によって互いに類似します。
![Rendered by QuickLaTeX.com \displaystyle A= \begin{pmatrix}-1&2\\[1.1ex] 3&1\end{pmatrix} \qquad B= \begin{pmatrix}-5&-3\\[1.1ex] 6&5\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4978e1117b69063b63256a0663eaf207_l3.png)
![Rendered by QuickLaTeX.com \displaystyle P= \begin{pmatrix}2&1\\[1.1ex] -1&0\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6344f1d5a14dd381ab105bcb52827455_l3.png)
これらが相互に類似した行列であることを示すには、まず P の逆行列を計算する必要があります。
![Rendered by QuickLaTeX.com \displaystyle P^{-1}= \begin{pmatrix}0&-1\\[1.1ex] 1&2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c49a4a995246e782635e2e2b43302798_l3.png)
次に、2 つの行列の類似性を定義する行列積を実行することで、それらが類似していることを確認します。
![]()
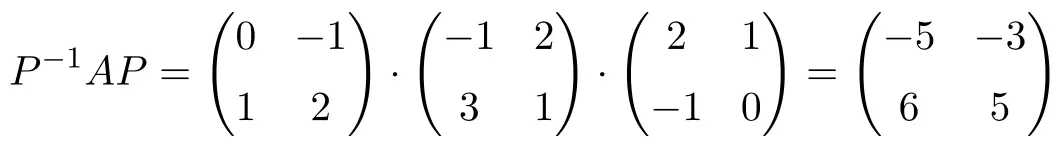
![]()
✅
はい、相似関係が成り立つので、相似行列になります。
同様の行列特性
2 つの類似した行列 A と B は、次の特性を共有します。
- 同じランクです。
![]()
- 2 つの行列の行列式は同じです。
![]()
- 同じトレースです。
![]()
- 同じ固有値(または固有値)。ただし、固有ベクトル (または固有ベクトル) は通常異なります。
- 同じ特性多項式と最小多項式。
- 行列の転置は元の行列と同様です。
- 行列 B は、行列 A の行に基本演算を適用することによって見つけることができ、逆も同様です。
- 明らかに類似性が反映されています。つまり、A が B に似ている場合、B も A に似ています。
- さらに、行列の相似性も対称です。つまり、行列 P で A (B) に似た行列が得られるのであれば、同じ行列 P でも B (A) に似た行列が得られます。
![]()
![]()
- さらに、類似性は推移的です。したがって、行列 A が行列 B に似ており、行列 B が行列 C に似ている場合、行列 A も行列 C に似ています。
![Rendered by QuickLaTeX.com \left. \begin{array}{l}A\sim B \\[2ex] B \sim C \end{array}\right\} \longrightarrow A \sim C](https://mathority.org/wp-content/ql-cache/quicklatex.com-a9f845ee4a4c9e72220ecb4033ea9640_l3.png)
- 最後に、各ダイは鋸歯状のダイに似ています。そして、この特性から次の結果を導き出すことができます。すべての正方行列は三角行列に似ています。
合同行列
一方、行列間には非常によく似た関係がもう 1 つありますが、これは逆行列ではなく転置行列です。これを合同といいます。
次の等式が満たされる可逆行列 P が存在する場合、2 つの行列 A と B は合同です。
![]()
ご覧のとおり、これは同様の行列に似ていますが、行列が転置されています。