非対称行列 - マソリティ

このページでは、反対称行列とは何かについて説明します。さらに、いくつかの例とその典型的な構造を見て完全に理解することができます。また、反対称行列の行列式の計算の特殊性と、このタイプの行列のすべての特性についても説明します。そして最後に、正方行列を対称行列と別の非対称行列の和に分解する方法を発見します。

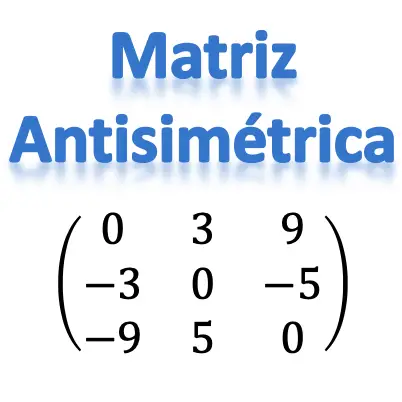
反対称行列とは何ですか?

非対称行列の定義は次のとおりです。

非対称行列は、転置が行列の負の値に等しい正方行列です。

$A^t = -A$

金

$A^t$

の転置行列を表します

$A$

そして

$-A$

マトリックスです

$A$

すべての要素の符号が変更されました。

反対称行列の例

反対称行列の概念を理解したら、それをよりよく理解するために反対称行列の例をいくつか見ていきます。

2 × 2 次の非対称行列の例

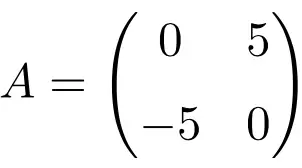
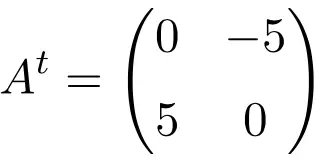
次元 3×3 の非対称行列の例

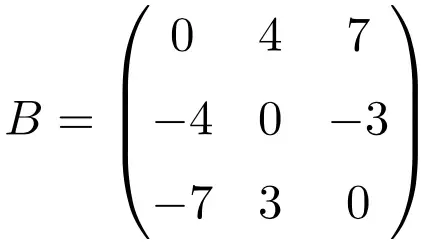
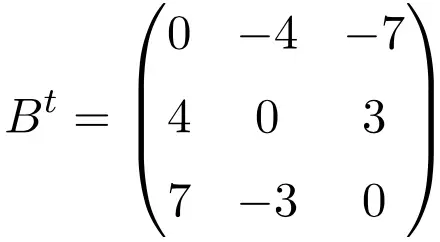
サイズ 4×4 の非対称行列の例

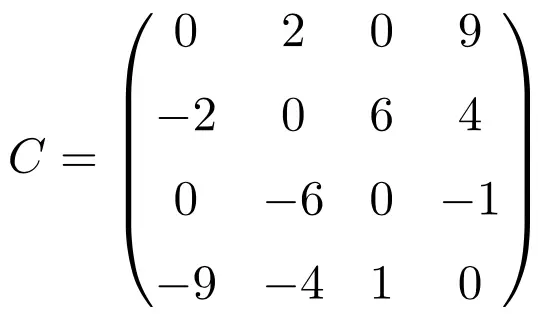
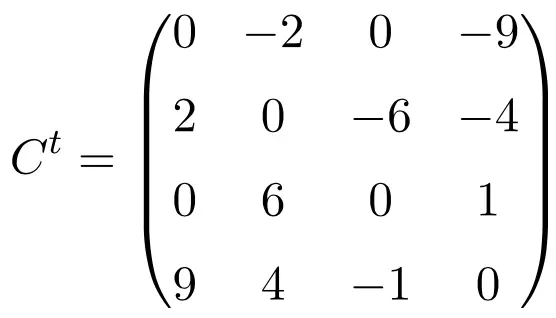
これら 3 つの行列を転置すると、転置された行列は符号を変更したそれぞれの元の行列と同等であるため、それらが非対称であることが検証されます。

反対称行列の構造

非対称行列の条件が満たされるには、それらは常に同じタイプの構造を持つ必要があります。主対角の数値はすべてゼロに等しく、行iと列jの要素は行jと列の要素の負の数です。私は。つまり、反対称行列の形式は次のとおりです。

$\displaystyle \begin{pmatrix} 0 & a & b & \cdots & c\\[1.1ex]-a & 0 & d & \cdots &e\\[1.1ex]-b & -d & 0 & \cdots & f\\[1.1ex]\vdots & \vdots & \vdots & \ddots & \vdots\\[1.1ex] -c & -e & -f & \cdots & 0\end{pmatrix}$

したがって、非対称行列の主対角線は非対称軸として機能します。これが、この特定のマトリックスの名前の由来です。

反対称行列の行列式

非対称行列の行列式は、その行列の次元に依存します。これは、行列式の特性によるものです。

$\displaystyle \text{det}(A)=\text{det}(A^t)=\text{det}(-A)=(-1)^n \text{det}(A)$

したがって、非対称行列が奇数次の場合、その行列式は 0 に等しくなります。一方、非対称行列が偶数次元の場合、行列式は任意の値を取ることができます。

したがって、奇数次元の非対称行列は特異行列または縮退行列です。一方、偶数次の非対称行列は正則行列です。

反対称行列の性質

非対称行列の特徴は次のとおりです。

2 つの反対称行列を加算 (または減算) すると、別の反対称行列が得られます。 2 つの加算 (または減算) 行列を転置することは、各行列を個別に転置することと同じであるため、次のようになります。

$\displaystyle \left(A+B\right)^t = A^t+B^t = -A-B$

非対称行列にスカラーを乗算すると、別の非対称行列も生成されます。

非対称行列の累乗は、非対称行列または対称行列に相当します。指数が偶数の場合、べき乗の結果は対称行列になりますが、指数が奇数の場合、べき乗の結果は非対称行列になります。対称行列とは何かについては、このリンクで参照できます。

非対称行列のトレースは常にゼロに等しくなります。

非対称行列とユニタリ行列の合計により、可逆行列が生成されます。

$\displaystyle \text{det}(A+I)\neq 0$

反対称行列の実固有値 (または固有値) はすべて 0 です。ただし、反対称行列は複素固有値を持つこともできます。

すべての非対称行列は正規行列です。したがって、それらは、非対称行列はユニタリ行列によって対角化できるというスペクトル定理の対象となります。

正方行列の対称行列と非対称行列への分解

正方行列の特別な特徴は、対称行列と非対称行列の和に分解できることです。

これを可能にする式は次のとおりです。

$\displaystyle \begin{array}{c} C = S + A \\[2ex] S = \cfrac{1}{2}\cdot (C+C^t) \qquad A = \cfrac{1}{2} \cdot (C-C^t)\end{array}$

ここで、C は分解したい正方行列、C^はその転置行列、最後に S と A はそれぞれ行列 C が分解される対称行列と非対称行列です。

以下に、公式を示すための解決済み演習があります。次の行列を分解してみましょう。

$\displaystyle C=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

次の式を使用して対称行列と非対称行列を計算します。

$\displaystyle S=\cfrac{1}{2}\cdot (C+C^t)= \begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}$

$\displaystyle A=\cfrac{1}{2}\cdot (C-C^t)= \begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}$

そして、2 つの行列を加算することで方程式が満たされていることを確認できます。

$\displaystyle C=S+A \quad ?$

$\displaystyle\begin{pmatrix} 1& 1 \\[1.1ex] 1 &2\end{pmatrix}+\begin{pmatrix} 0& 4 \\[1.1ex] -4 &0\end{pmatrix}=\begin{pmatrix} 1& 5 \\[1.1ex] -3 &2\end{pmatrix}$

$\displaystyle C=S+A$

✅