無理関数または根関数 -

このページでは、無理関数 (根関数とも呼ばれます) とは何か、およびこのタイプの関数のすべての特徴について説明します。また、根関数または無理関数の定義域を計算する方法を発見し、さらに、グラフ上でそれらを表現する方法を例とともに確認し、演習や問題を段階的に解決して練習することができます。

非合理 (またはラジカル) 関数とは何ですか?

無理関数は根関数と同じことを意味するため、これらは次の定義を共有します。

無理関数は根関数とも呼ばれ、根の記号の下に独立変数 x を持つ関数です。

すでにご存知のとおり、ルートの結果はプラスまたはマイナスになる可能性があります。したがって、無理数 (またはラジカル) 関数の表現には 2 つの可能な曲線があります。

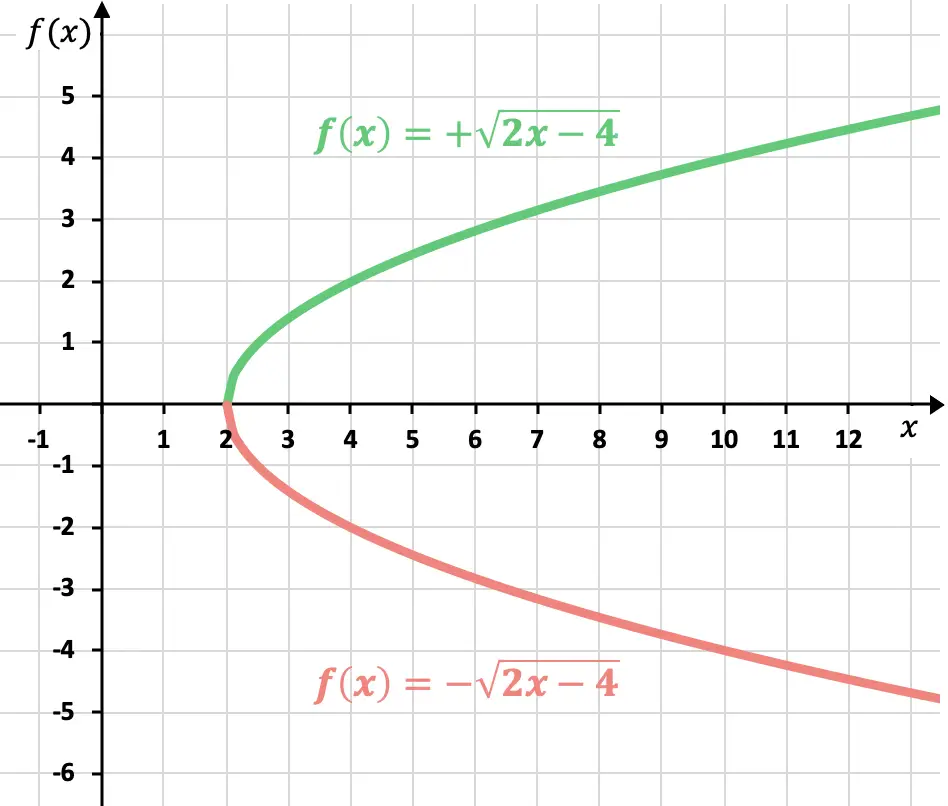
ただし、符号が指定されていない場合は、正の関数が表現されることになります。

一方、無理関数を有理関数と混同しないでください。これらは非常によく似た名前ですが、まったく異なるタイプの 2 つの関数です。

無理関数または根関数の領域

ルートを持つ関数の定義域は、ルートインデックスのパリティに依存します。つまり、根号インデックスが偶数であるか奇数であるかに依存します。

偶数インデックスのルートを持つ関数のドメイン

ご存知のとおり、負の数には根 (偶数のインデックス) がありません。したがって、偶数のインデックスを持つ根関数は、その内容が 0 以上である限り存在します。

例として、次の根関数または無理関数の定義域がどのように計算されるかを見てみましょう。

$f(x)=\sqrt{x-4}$

これはラジカル偶数インデックス関数であるため、その内容が正またはゼロである場合を確認する必要があります。

$x-4\ge 0$

不等式を解きます。

$x\ge 4$

したがって、この関数は x が 4 以上の場合に常に存在し、次の間隔で示されます。

$\text{Dom } f= [4,+\infty)$

奇数のインデックスのルートを持つ関数のドメイン

奇数のインデックスを持つ無理関数では、負の数の奇数のインデックスのルートが存在するため、この問題は発生しません。

$\sqrt[3]{-8}=-2$

したがって、奇数のインデックスの根関数は、 xの任意の値に対して存在します。言い換えれば、ドメインは実数のみで構成されます。

たとえば、インデックスが奇数である次の根関数の定義域を計算します。

$f(x)=\sqrt[3]{3x-4}$

これは奇数のインデックスを持つ無理関数であるため、その定義域は実数で構成されます。

$\text{Dom } f= \mathbb{R}$

無理関数または根関数を表現する方法

例を使用して、グラフ上で根を持つ関数を表す方法を見てみましょう。

次の根関数または無理関数をグラフにプロットします。

$f(x)=\sqrt{x+2}$

最初に行うことは、関数のドメインを見つけることです。これは平方根なので、負の数の平方根は存在しないため、そこに含まれるものはすべて正でなければなりません。したがって、ラジカル関数は、その内容が 0 以上である限り存在します。

$x+2\ge 0$

$x\ge -2$

したがって、関数の定義域は -2 以上のすべての数値で構成されます。つまり、次のようになります。

$\text{Dom } f = [-2,+\infty)$

関数のドメインがわかったら、値のテーブルを作成します。明らかに、計算するポイントが多ければ多いほど、関数の表現はより正確になります。ただし、ドメイン間隔内の 3 つまたは 4 つのポイントを計算すれば十分です。

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

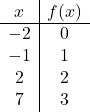
得られた点をグラフ上に表現します。

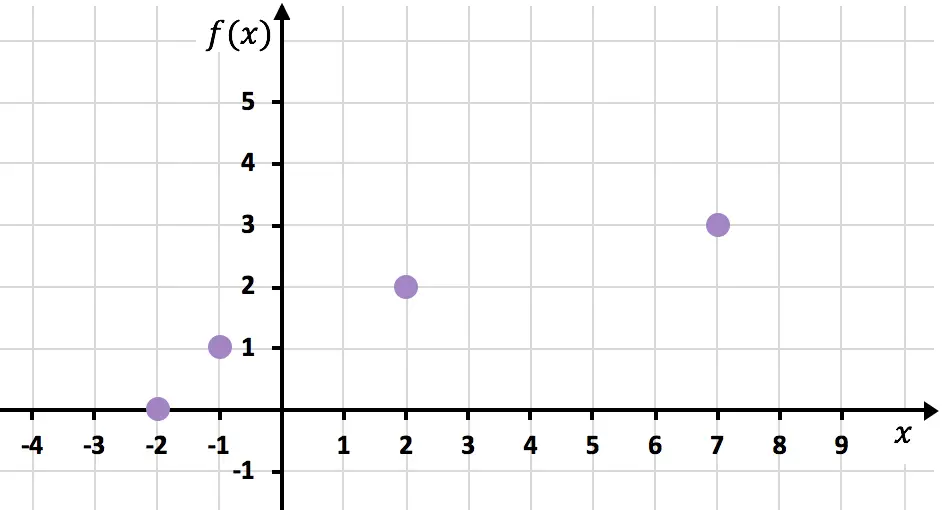
最後に、点を結合して曲線を延長し、関数が成長し続けることを示します。

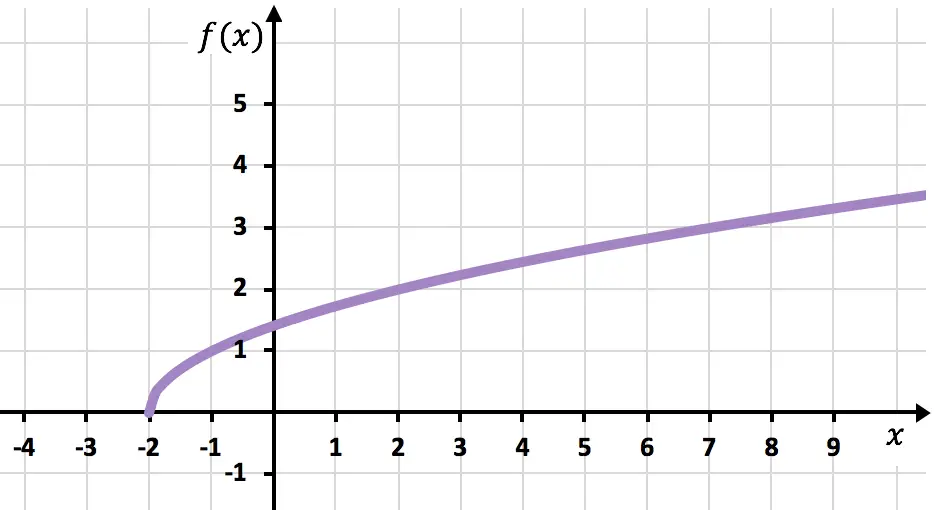
非合理関数または急進関数に関する演習問題を解決しました。

演習 1

次の根関数の定義域を求めます。

$\sqrt{3x+6}$

解決策を見る

負の数の平方根は存在しません。したがって、関数はルート引数が正またはゼロの場合に存在します。

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

演習 2

次の無理関数の定義域を求めます。

$\sqrt{-x+2}$

解決策を見る

負の数の平方根には実際の解はありません。したがって、ルートの内容が正またはゼロである限り、関数は存在します。

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

不等式で乗算または除算する負の数の辺を変更する場合は、不等号の符号も回転する必要があることに注意してください。

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

演習 3

次の無理関数をグラフにプロットします。

$f(x)= \sqrt{x-1}$

解決策を見る

まず最初に、関数の定義域を計算する必要があります。

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

次に、ドメイン範囲内の関数の値を指定して、値の配列を作成します。

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

最後に、点をプロットし、グラフ上に関数をプロットします。

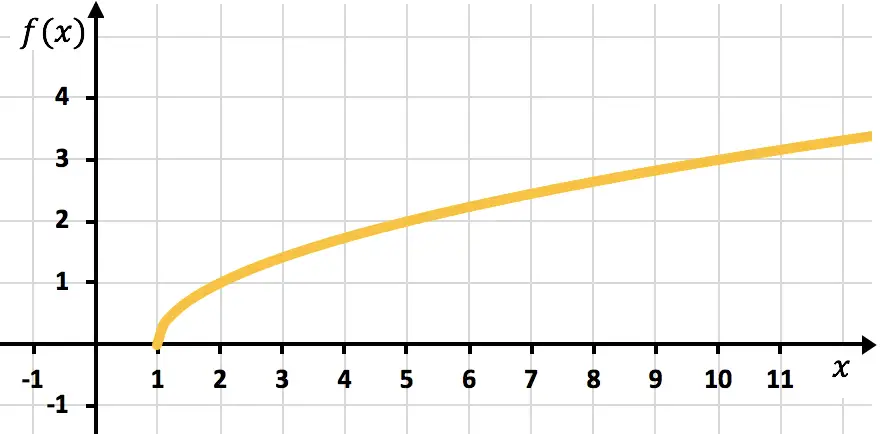
演習 4

次の無理関数または根関数をグラフにします。

$f(x)= -2\sqrt{x}+3$

解決策を見る

まず最初に、関数の定義域を計算する必要があります。

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

次に、ドメイン範囲内の関数の値を指定して、値の配列を作成します。

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

最後に、点をプロットし、グラフ上に関数を描画します。

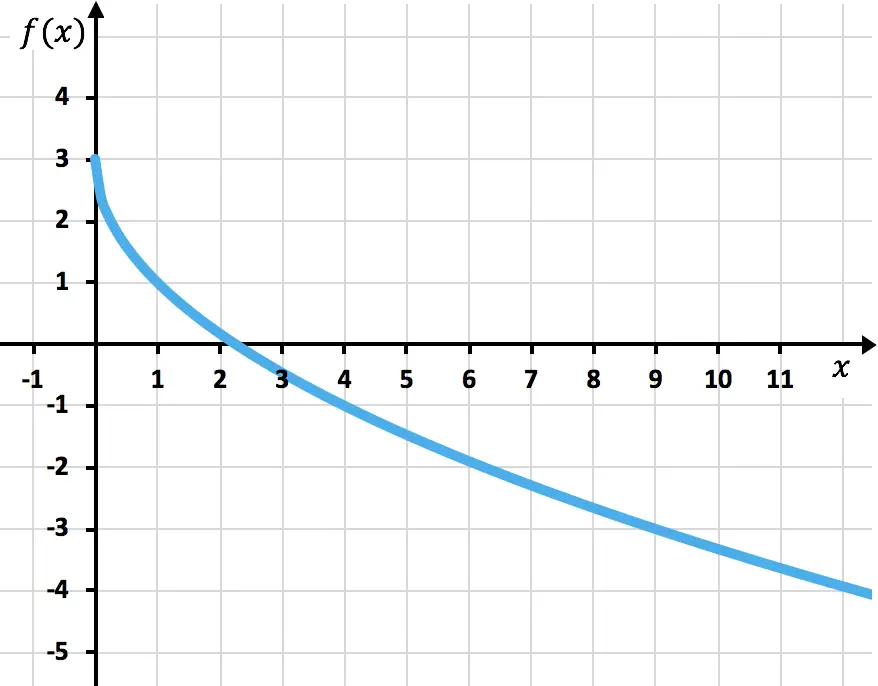
演習 5

次の無理関数または根関数をグラフにします。

$f(x)= \sqrt{-x+5}$

解決策を見る

関数をプロットする前に、関数の定義域を計算する必要があります。

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

不等式で乗算または除算する負の数の辺を変更する場合は、不等号の符号も変更する必要があることに注意してください。

$x\le5$

$\text{Dom } f = (-\infty,5]$

ここで、関数のドメインに属する点で関数を評価することにより、値のテーブルを構築します。

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

最後に、点を表し、グラフ上に関数をペイントします。

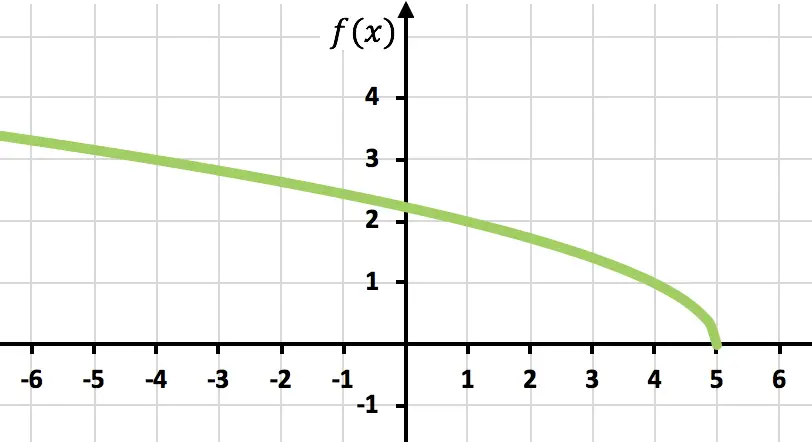
演習 6

次の無理関数または根関数をグラフにプロットします。

$f(x)= \sqrt{x^2-5x+4}$

解決策を見る

まず関数の定義域を計算する必要があります。

$x^2-5x+4\ge 0$

この場合、2 次不等式が得られたため、それを解くために 2 次方程式の公式を適用する必要があります。

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

得られたルートを使用して、行を 3 つの部分に分割します。

そして、不等式の各セクションに数値を代入して、どのセクションが不等式を満たしているのか、したがってドメインに属しているのかを確認します。

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

したがって、不等式を尊重するセクションは辺のセクションです。

したがって、関数のドメインは次のようになります。

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

関数の定義域を計算したら、定義域の範囲内の関数の値を与える値のテーブルを作成します。

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

最後に、取得した点をグラフ上に表し、関数をプロットします。

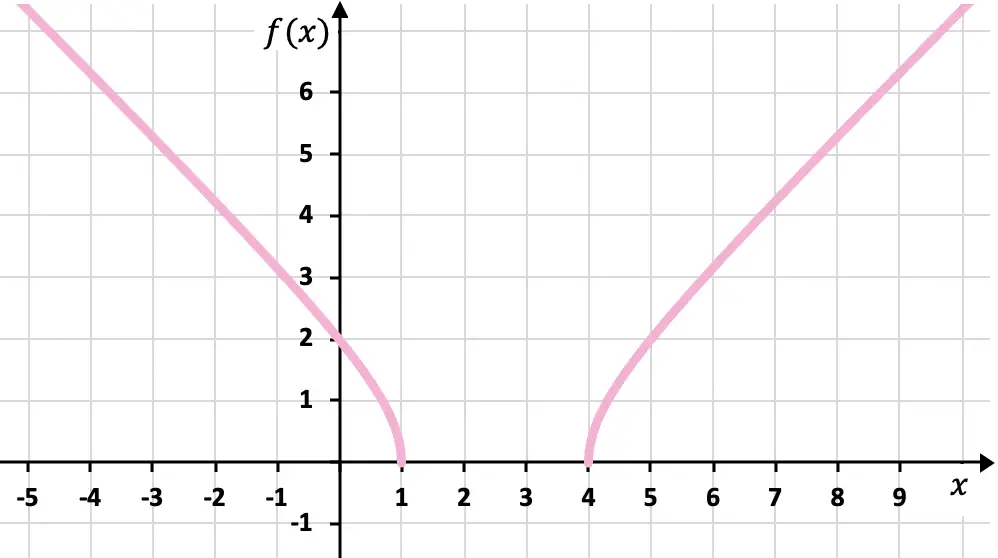
演習 7

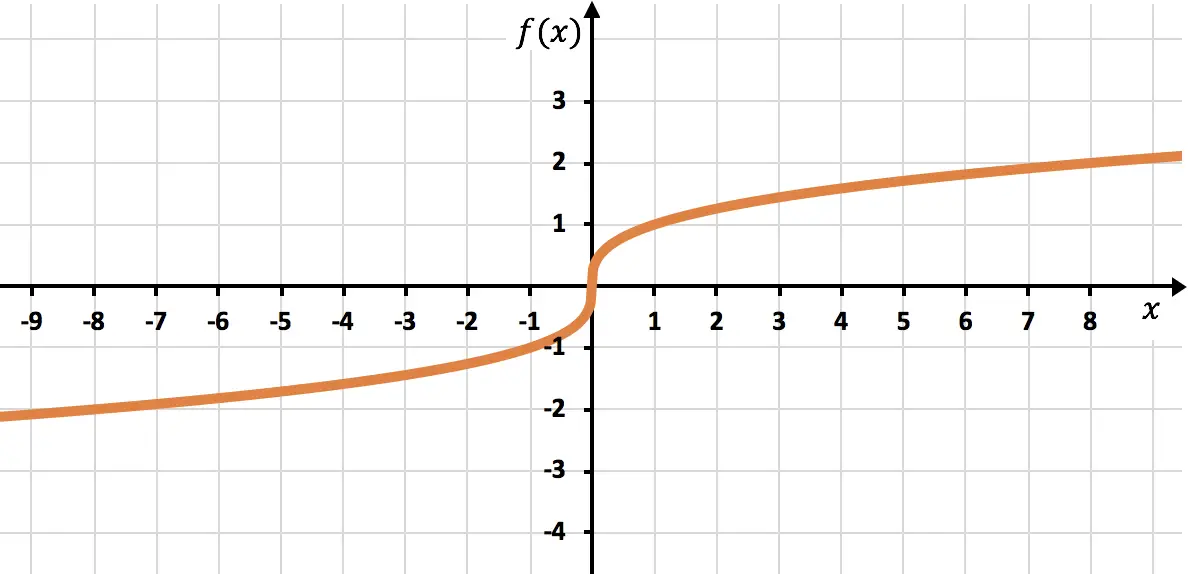
ルートによって形成される次の関数をグラフ上に表します。

$f(x)= \sqrt[3]{x}$

解決策を見る

これはルートのインデックスが奇数である無理関数であるため、関数の定義域は実数で構成されます。

$\text{Dom } f = \mathbb{R}$

したがって、任意の点を取得して値の表を作成できます。この場合、立方根であるため、多くの点を探します。

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

最後に、見つかった点をプロットし、グラフ上に関数をプロットします。

演習 8

無理数 (またはラジカル) 関数に関連する次の問題を解きます。

携帯電話のバッテリーの消費量は次の関数で求められます。

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

ここで、消費量はミリアンペア (mA) で表され、

$t$

経過時間 (分) です。

定数の値を決定する

$K$

4 分後の消費量は 35 mA になります。

解決策を見る

4 分後の消費量が 35 mA であるということは、t が 4 の場合、f(t) は 35 であることを意味します。つまり、f(4)=35 になります。

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

次に、得られた方程式を解く必要があります。よく見ると根があるので無理数です。このタイプの方程式では、最初に片側の根を分離することになります。この場合、根はすでに分離されています。分離したら、方程式の両辺を二乗する必要があります。

$\left( \sqrt{4-K} \right)^2= 35^2$

次に、ルートを単純化します。

$4-K= 35^2$

そして、次の方程式を解きます。

$4-K= 1125$

$4-1225=K$

$\bm{-1221=K}$

最後に、無理数方程式では、解を検証する必要があります。したがって、最初の方程式に K=-1221 を代入する必要があります。

$\sqrt{4-K} = 35 \ \xrightarrow{K \ = \ -1221} \ \sqrt{4-(-1221)} = 35$

$\sqrt{4+1221} = 35$

$\sqrt{1225} = 35$

$35 = 35$

等式が成り立つので、Ｋ＝－１２２１が解となる。

非合理 (またはラジカル) 関数とは何ですか?

無理関数または根関数の領域

偶数インデックスのルートを持つ関数のドメイン

奇数のインデックスのルートを持つ関数のドメイン

無理関数または根関数を表現する方法

非合理関数または急進関数に関する演習問題を解決しました。

演習 1

演習 2

演習 3

演習 4

演習 5

演習 6

演習 7

演習 8

コメントする 返信をキャンセル

コメントする返信をキャンセル