多項式因数分解とは何ですか?これは、多項式をより単純な因子または式に分解できる数学的手法です。この単純化のおかげで、いくつかの代数式間の演算をより簡単かつ快適に実行できるようになります。したがって、この記事では、多項式を因数分解するさまざまな方法と、考えられるすべての因数分解のケースについて説明します。
多項式を因数分解するにはどうすればよいですか?
独自の解構造を持つ因数分解手法が多数ありますが、最終的には同じものに依存します。さらに、多項式構成に関するさまざまなケースも見つけることができます。そのため、次のセクションでは、存在するすべてのプロシージャと、それぞれのプロシージャをいつ使用するかについて説明します。最後に実際の例に適用して概念の習得を完了します。
ルフィニの法則を使用して多項式を因数分解する
多項式の因数分解に最もよく使用される方法は、使いやすく結果がすぐに見つかるルッフィーニの法則です。通常は、この手法を使用して 2 を超える次数の多項式を因数分解するか、場合によっては 2 次の多項式を因数分解することもあります。この多項式の根を非常にグラフィカルに取得できるためです。ただし、この使用法については、このタイプの数式の根に焦点を当てた次のセクションで説明します。
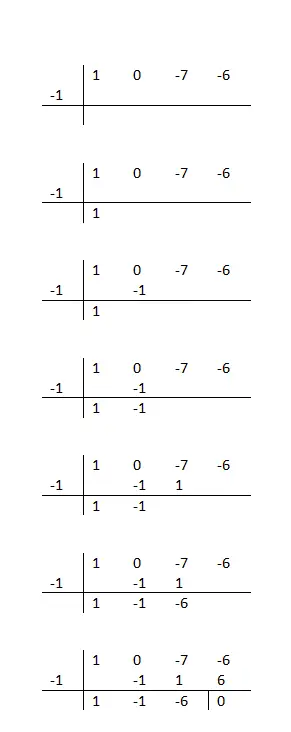
ルフィニで多項式を因数分解するにはどうすればよいですか?
基本的に、被除数の係数を水平線に、多項式の可能な根の値を横に書く必要があります。可能であると言うのは、ゼロに等しい剰余を得ることができる約数を探す必要があるからです。それ以外の場合、この番号は有効なルートではないため、試行を続ける必要があります。
ヒントとして、独立項の約数 (水平線の最後の値) のみを試すことをお勧めします。したがって、選択した数値が正しいかどうかを知るには、次の一連の計算に従うだけで済みます。
係数を減らし、テストしている根を掛けて、次の係数の下に書き込み、垂直加算を行います。これらの手順を最後まで繰り返すだけで、完了すると、この値が正しいかどうかがわかります。剰余がゼロになる数値のみが有効となるためです。
従う必要がある数学的手順がよくわからない場合は、このテキストの左側の列にある例を参照してください。また、次の多項式を因数分解してみることをお勧めします: x³ + 2x² – x – 2 (例に基づく)。最後に、演習を正しく解いたかどうかを知るために、結果を次の結果と比較できます。
- 過剰な式 = x² + 3x + 2
- 余り = 0
ここで、因数分解におけるルフィニの応用について簡単に説明します。ただし、この数学的リソースがどのように使用されるかを詳しく知りたい場合は、リンクした最後の記事にアクセスすることをお勧めします。そこではすべてが非常に詳しく説明されています。そうは言っても、ルフィニの法則を使用して多項式を因数分解する方法を説明することから始めましょう。
- グリッドを描きます。上の画像でわかるように、ルッフィーニを作るためのボックスを作成します。基本的に、式の係数を水平方向に並べて、ゼロ値を持つ係数を残さずに記述する必要があります。最終的には、画像のものと同様の表現が得られますが、多項式の値が使用されます。
- 根を計算します。構造を描画し、すべての数値が正しく書かれていることを確認したら、根の計算に進みます。このリスト (写真付き) のすぐ上で説明した計算シーケンスに従って、根を見つける必要があります。
- 根を (x – a) の形式で表現します。多項式の根がすべて得られたら、次の形式 (x – a) で表現する必要があります。 a が取得した値であることを考慮すると、たとえば、結果として x = 2、x = -2、および x = 4 を抽出した場合、(x – 2)、(x + 2)、および ( × – 4)。
- すべての因子を 1 つの式に収集します。最終的に、すべての根がすでに正しい形式で表現されている場合、それらを 1 つの代数式に収集するだけで済みます。前の例を続けると、(x – 2) · (x + 2) · (x – 4) のようになります。
多項式の根を使用して多項式を因数分解します。
多項式の根本概念については、ルフィニのセクションで半分説明しました。ただし、正確な定義は次のようになります。多項式 P(x) の根は数値 a であり、 P(a) = 0となります。したがって、これは問題の関数または多項式をキャンセルできる数です。要約すると、多項式を因子の積に分解するために使用されると言えます。
たとえば、次の式 x² − x − 2 が与えられ、ルフィニの法則を使用するか、単純に二次方程式 x² − x − 2 = 0 を解くことによって因数分解すると、2 つの x 値 = -1 と が得られます。 x = 2 なので、これらを (x – a) の形式に変更して組み合わせると、次の式に到達します: (x + 1) (x − 2)、つまり因数分解された多項式。また、式が複数の項で構成されている場合でも、これを 2 より大きい次数の多項式に適用できます。
共通因数抽出による多項式の因数分解
独立した項のない多項式、またはすべての項に共通の約数を持つ式を因数分解する場合は、この手法を使用して多項式を単純化できます。これには基本的に、式全体に分配プロパティを適用し、その繰り返しの共通因数を削除し、多項式全体を乗算して加算することが含まれます。以下に、最初に説明したケース (独立項のない多項式) の例を示します。
2×3 + 10×2 – 6x = 2x (x2 + 5x – 3)
共通因数の二重抽出
共通因子の抽出は、複数の変数を含むより複雑な因子を抽出することによっても実行できます。また、メイン式自体から派生した多項式を抽出することもできます。因数抽出の目的は代数式を可能な限り単純化することであるため、このタイプの演算を実行する場合は制限を設定しないことが重要です。
注目すべき恒等式を使用した多項式の因数分解
注目すべき製品は、多項式が一種の単純化された代数式であるため、因数分解に役立ちます。したがって、これらは、長い多項式からいくつかの項で構成される小さな式に直接変換するのに役立ちます。したがって、注目すべきアイデンティティの公式を学習し、いつ使用できるかをすぐに特定できるようにすることを強くお勧めします。したがって、Ruffini またはその他の方法を使用してファクタリングする時間を節約できます。次に、学習する必要がある 3 つのルールについて説明します。
- 二乗の差: a² – b² = (a + b) · (a – b)
- 和の二乗: a² + 2ab + b² = (a + b)²
- 減算二乗: a² – 2ab + b² = (a – b)²
グループ化による多項式の因数分解
場合によっては、 x² – ax – bx + abという構造の多項式が見つかることがあります。これは、共通因数 x (x – a) – b (x – a) を削除することで簡略化できます。そして、もう一度共通因数を取ると、(x – a) · (x – b) のようにさらに単純化できます。したがって、この多項式の根は x = a および x = b になります。ご覧のとおり、このタイプの代数式は、因数分解と使用が非常に簡単な構造になっています。
多項式因数分解の演習
最後に、多項式の因数分解を練習できる一連の演習を提供します。こうすることで、今日説明した理論をよりよく理解できるようになります。簡単に言うと、ノートブック内の演習を解いて、その結果を以下に提供する結果と比較するだけです。
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2