この記事では、関数の微分可能性、つまり関数が微分可能かどうかを研究する方法を学びます。さらに、微分可能性と関数の連続性の関係も見ていきます。そして最後に、区分関数の微分可能性を研究します。
関数の微分可能性と連続性
ある点における関数の連続性と微分可能性は次のように関係します。
- 関数がある点で微分可能である場合、その関数はその点で連続です。
- 関数がある点で連続でない場合、その点では微分可能でもありません。
ただし、この定理の逆は誤りです。関数がある点で連続であるからといって、その点で常に微分可能であるとは限りません。
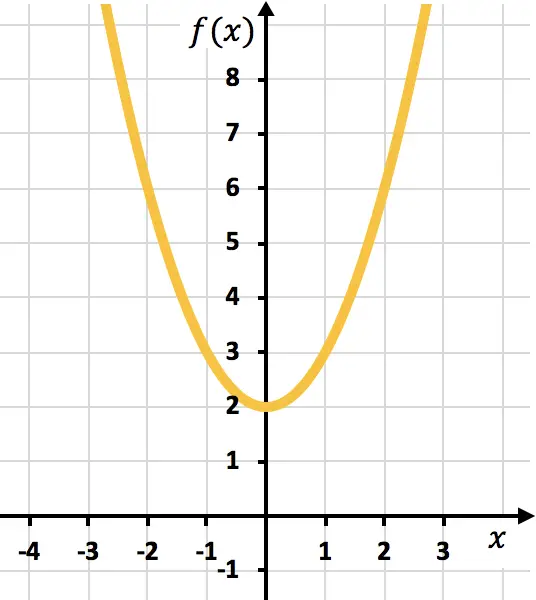
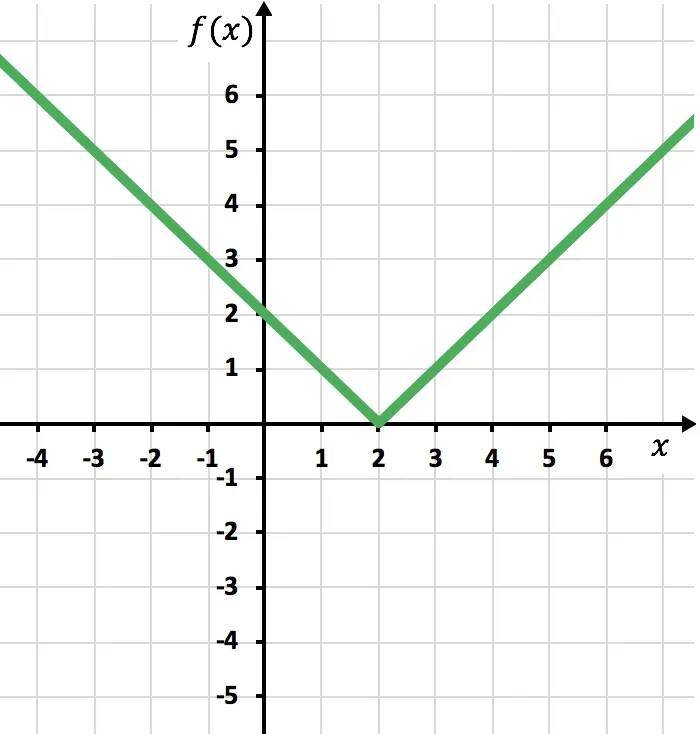
また、関数がある点で微分可能かどうかをグラフ表示から確認することもできます。
- 滑らかな点であれば、この点で関数は微分可能です。
- それが角点の場合、関数は連続ですが、この点では微分可能ではありません。
x=0 での平滑化ポイント:
この段階では連続微分可能な関数です。
x=2 の角度点:
関数は連続ですが、この段階では微分できません。
区分関数の微分可能性
関数の連続性と微分可能性の関係がわかれば、区分的に定義された関数の微分可能性を研究する方法がわかります。
区分関数がある点で微分可能かどうかは、その点での横導関数を計算することでわかります。
- ある点における横導関数が等しくない場合、その関数はその点では微分可能ではありません。
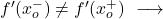
では控除対象外です
- ある点での横導関数が一致する場合、その関数はその点で微分可能です。
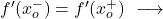
はい、微分可能です
注:ある点で関数が微分可能であるためには、その関数がその点で連続的である必要があります。したがって、横導関数を計算する前に、関数がその時点で連続であることを確認する必要があります。ある時点で連続性がどのように調査されるかわからない場合は、次のリンクでその方法を確認できます。
➤参照: ある点における関数の連続性
次に、点で区分的に定義された関数の導関数を計算する方法の例を見てみましょう。
- 点 x=2 で区分的に定義された次の関数の連続性と微分可能性を調べます。
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
2 つの部分の関数はそれぞれの区間で連続していますが、臨界点 x=2 で関数が連続しているかどうかを確認する必要があります。これを行うには、次の点で関数の横方向の制限を解決します。
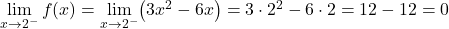
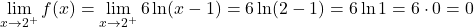
臨界点での横方向の限界でも同じ結果が得られたため、関数は点 x=2 で連続です。
関数が x=2 で連続であることがわかったら、その点での関数の微分可能性を調べます。これを行うには、分割して定義された関数の横導関数を計算します。
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
ここで、臨界点で各横導関数を評価します。
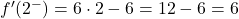
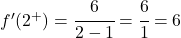
2 つの横導関数は同じ結果をもたらしたので、関数は x=2 で微分可能であり、導関数の値は 6 になります。
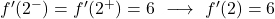
一方、横微分によって異なる結果が得られた場合、これは関数が x=2 で微分可能ではないことを意味します。言い換えれば、この時点では導関数は存在しません。
最後に、絶対値関数は区分的に定義することもできるため、この手順は絶対値関数の微分可能性を調べるのにも有効であることを覚えておいてください。絶対値関数をチャンクに変換する方法はここで確認できます。
➤参照: 絶対値を使用して関数を区分的に定義する方法
関数の微分可能性に関する解決された演習
演習 1
次の区分関数の連続性と微分可能性を調べてください。
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
2 つの部分の関数は連続ですが、関数が臨界点 x=1 で連続であるかどうかを確認する必要があります。これを行うために、次の点で関数の横方向の制限を解決します。
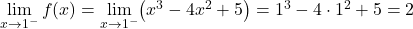
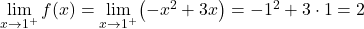
臨界点における 2 つの横方向の限界は同じ結果を与えるため、関数は x=1 で連続です。
関数が臨界点で連続であることがわかったら、同じ点で微分可能かどうかを調べます。したがって、横導関数を計算します。
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
そして、x=1 で 2 つの横導関数を評価します。
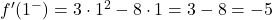
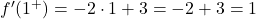
横導関数は点 x=1 では一致しないため、この点では関数は微分可能ではありません。
演習 2
セクションで定義されている次の関数の微分可能性と連続性を分析します。
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
解決策を見る
2 つのセクションの関数はその区間では連続ですが、定義 x=1 の変化の臨界点で関数が連続であるかどうかを知ることも必要です。したがって、この時点で関数の横方向の限界を定義します。
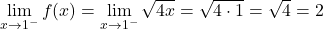
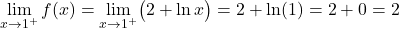
臨界点における 2 つの横方向の限界は同じ結果を与えるため、関数は x=1 で連続です。
ここで、横導関数を計算することによって、関数がこの時点で微分可能かどうかを調べます。
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
x=1 で 2 つの横導関数を評価します。
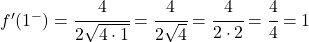
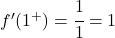
横導関数は等しいため、関数は x=1 で微分可能であり、導関数の値は 1 になります。
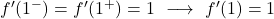
演習 3
次の区分関数が連続的であり、領域全体にわたって微分可能であるかどうかを判断します。
*** QuickLaTeX cannot compile formula:
\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2+2x+1 & \text{si} & x\leq -1 \\[2ex] 2x+2 & \text{ si} & -1<div class="wp-block-otfm-box-spoiler-start otfm-sp__wrapper otfm-sp__box js-otfm-sp-box__closed otfm-sp__E6F9EF" role="button" tabindex="0" aria- expanded="false" data-otfm-spc="#E6F9EF" style="text-align:center"><div class="otfm-sp__title"> <strong>View solution</strong></div>< /div> The functions of all three parts are continuous, but we still need to check if the function is continuous at critical points. We therefore first check the continuity of the function at the point x=-1 by solving the lateral limits at this point:
*** Error message:
Missing $ inserted.
leading text: \displaystyle
Missing { inserted.
leading text: ...="wp-block-otfm-box-spoiler-start otfm-sp__
Missing { inserted.
leading text: ...ox-spoiler-start otfm-sp__wrapper otfm-sp__
Missing { inserted.
leading text: ...m-sp__wrapper otfm-sp__box js-otfm-sp-box__
Missing { inserted.
leading text: ...fm-sp__box js-otfm-sp-box__closed otfm-sp__
You can't use `macro parameter character #' in math mode.
leading text: ...="0" aria-expanded="false" data-otfm-spc="#
Missing { inserted.
leading text: ...e="text-align:center"><div class="otfm-sp__
Please use \mathaccent for accents in math mode.
leading text: ...g></div></div> The functions of the three parts
Please use \mathaccent for accents in math mode.
leading text: ...are continuous, but we still need to see
\lim\limits_{x\to -1^-} f(x) = \lim\limits_{x\to -1^-} \bigl(x^2+2x+1\bigr) = (-1)^ 2+2(-1)+1 =0 \lim\limits_{x\to -1^+} f(x) = \lim\limits_{x\to -1^+} \bigl(2x+2\bigr ) = 2(-1)+2=0
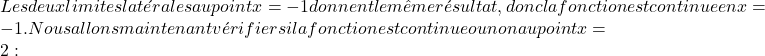
\lim\limits_{x\to 2^-} f(x) = \lim\limits_{x\to 2^-} \bigl(2x+2\bigr) = 2\cdot 2+2=4+2= 6 \lim\limits_{x\to 2^+} f(x) = \lim\limits_{x\to 2^+} \bigl( -x^2+8x\bigr) = -2^2+8\ cdot 2 = -4+16=12
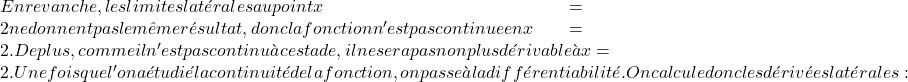
\displaystyle f'(x)= \left\{ \begin{array}{lcl} 2x+2 & \text{si} & x\leq -1 \\[2ex] 2 & \text{si} & -1
この関数が x=2 で微分可能でないことはすでにわかっているので、必要なのは関数が x=-1 で微分可能かどうかを調べることだけです。これを行うために、次の点で 2 つの横導関数を評価します。
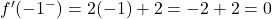
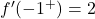
横微分は点 x=-1 で一致しないため、その点では関数は微分可能ではありません。
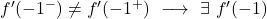
演習 4
次の区分関数が領域全体で連続かつ微分可能となるように、パラメーター a と b の値を計算します。
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
未知数の値が何であれ、関数は x=3 を除くすべての点で連続で微分可能です。x=3 では連続性と微分可能性をチェックする必要があります。
ある点で関数が連続であるためには、その点での 2 つの横方向の限界が一致する必要があります。したがって、臨界点での横方向の限界を評価します。
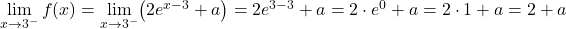
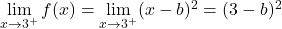
したがって、関数が連続であるためには、横方向の限界から得られる 2 つの値が等しくなければなりません。
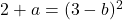
ここで、点 x=3 における微分可能性を分析します。横導関数を求めます。
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)
そして、臨界点で 2 つの横導関数を評価します。
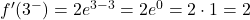
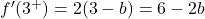
したがって、関数が x=3 で微分可能であるためには、横導関数から得られる値が等しくなければなりません。
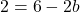
そして、この方程式を解くことで、b の値を見つけることができます。
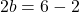
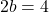
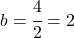
最後に、パラメーター b の値がわかったら、横方向の制限で以前に取得した方程式を解くことによって、パラメーター a の値を計算できます。
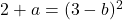
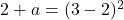
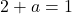
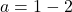
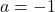
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
![]()
![]()
![]()
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
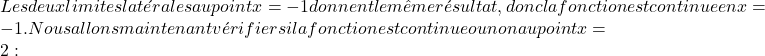
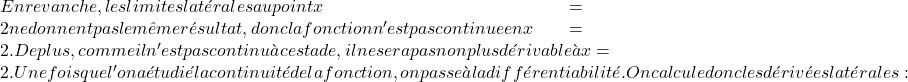
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)