この記事では、複合関数(または関数の合成)とは何かについて説明します。さらに、複合関数のいくつかの例と、このタイプの関数の定義域がどのように計算されるかを見ることができます。最後に、関数合成のプロパティといくつかのステップバイステップの演習を示します。
関数合成とは何ですか?
関数合成は、2 つ以上の関数で独立変数 (x) の同じ値を連続して評価することで構成されます。たとえば、関数 (gof)(x) を合成すると、合成関数 g[f(x)] が得られます。
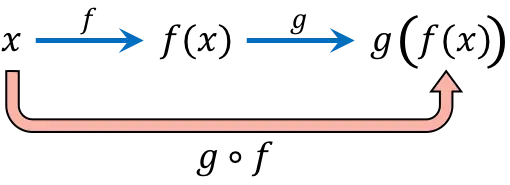
複合関数の式
![]()
「f は g で構成されている」または「f の後に g が続いている」と読みます。
関数の合成では順序が重要であることに注意してください。合成記号の右側にある関数が最初に適用されます。
![]()
次に合成記号の左側の関数
![]()
機能構成例
複合関数の定義を踏まえて、2 つの関数の合成を計算する方法の例を見てみましょう。
- 次の 2 つの異なる関数があるとします。
![]()
複合関数を計算する
![]()
そしてそれを評価します
![]()
機能の構成
![]()
これは、次の複合関数を実行する必要があることを意味します。
![]()
それを解決するには、次のように置き換えます
![]()
代数式で表すと次のようになります。
![]()
そして今、私たちは次の関数を取ります
![]()
そして次の式を入れます
![]()
どこにあるのか
![]()
![]()
このようにして、 gから構成される関数fをすでに計算しています。
![]()
最後に、複合関数を評価するには、
![]()
上記の値の関数のイメージを単純に計算します。
![]()
複合関数ドメイン
通常、関数に対して演算を実行すると、結果の関数のドメインは元の関数のドメインの共通部分になります。ただし、関数合成ではこの性質は満たされません。
関数合成の領域
![]()
関数の定義域内の x のすべての値のセットと同等です
![]()
のような
![]()
機能の領域に属します
![]()
![]()
したがって、複合関数の定義域を計算するには、まず各関数の定義域を個別に見つけてから、演算の結果として得られる関数の定義域を見つける必要があります。したがって、関数の合成領域は、前の数学的条件を満たすすべての値で構成されます。
👉 解決方法がわからない問題が発生した場合は、以下のコメント欄で質問してください。
関数合成の性質
複合関数には次の特徴があります。
- 関数の合成には結合特性があるため、次の方程式は常に真となります。
![]()
- 一般に、関数の合成は可換ではないため、演算の順序によって結果が決まります。
![]()
- 関数の合成の中立要素は恒等関数に対応します
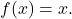
したがって、恒等関数で構成される関数は関数自体になります。
![]()
![]()
- 2 つの関数の合成の逆関数を計算することは、まず各関数の逆関数を求めてから合成関数を決定することと同じです。
![]()
- 逆関数は、関数とその逆関数の合成が恒等関数と同等であるため、複合関数の対称要素としても機能します。
![]()
- 2 つの関数の合成の導関数は、連鎖則を使用して計算されます。
![]()
➤参照: 連鎖ルールとは何ですか?
関数の構成に関する演習を解決しました
演習 1
次の 2 つの関数があるとします。
![]()
gと合成された関数fおよびfと合成された関数gの合成を計算します。
![]()
![]()
機能の構成
![]()
は、次の複合関数を計算することを意味します。
![]()
したがって、それを解決するには、次のように置き換えます
![]()
その表現について:
![]()
![]()
そして
![]()
これは、次の式で表されることを意味します。
![]()
変数を置き換える必要があります
![]()
のために
![]()
![]()
まだ:
![]()
一方、 fで構成される関数gを見つけるには、同じ手順を逆の順序で実行する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2e9be8f1bab4b7607441c7c1b7e3ad0c_l3.png)
この演習では、結果が関数が適用される順序に依存するため、複合関数が可換でないという特性も示します。
演習 2
次の 2 つの関数があるとします。
![]()
gと合成された関数fの合成を計算します。
![]()
gで構成される関数f は、次の複合関数を解くことを意味します。
![]()
したがって、関数 f(x) を次の式で置き換えます。
![]()
そして今、私たちは置き換えなければなりません
![]()
のために
![]()
関数 g(x) の式では次のようになります。
![Rendered by QuickLaTeX.com \begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bf0bb412f9088845027b57d83a91073d_l3.png)
つまり、関数合成の結果は次のようになります。
![]()
演習 3
次の 2 つの二次関数があるとします。
![]()
次の関数を組み合わせた結果を求めます。
![]()
![]()
次の複合関数を見つけることで構成されます。
![]()
したがって、複合関数を解くために、最初に計算します
![]()
![]()
![]()
したがって、
![]()
![]()
したがって、複合関数の値を見つけるには、単に計算する必要があります
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9fc21e0e44e696ed36cd6e9a535cff09_l3.png)
要約すると、関数合成問題の結果は次のようになります。
![]()
演習 4
次の 2 つの関数があるとします。
![]()
x=2 でgとfを合成した結果を求めます。
![]()
この場合、次の複合関数を計算する必要があります。
![]()
それで、最初に見つけます
![]()
![]()
![]()
それで、例えば
![]()
![]()
したがって、複合関数を解くには計算する必要があります。
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ec461a36a477af7bc703fd48bc3d4c2_l3.png)
結論として、複合関数を実行した結果は次のようになります。
![]()
演習 5
次の 3 つの関数があるとします。
![]()
次の 3 つの関数の構成を計算します。
![]()
表現
![]()
これは、次の複合関数を計算する必要があることを意味します。
![]()
したがって、最初に決定します
![]()
![Rendered by QuickLaTeX.com \begin{aligned}g\Big( f(x)\Big)&=g\Big(x+1 \Big)\\[2ex]&= 3(x+1)-5\\[2ex]&= 3x+3-5\\[2ex]&= 3x-2\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a0ab9465f2aebf9fb7c81298eab5b8ca_l3.png)
そして今計算します
![]()
。これを行うには、次から見つかった式を置き換えます。
![]()
が現れるところ
![]()
関数内で
![]()
![Rendered by QuickLaTeX.com \begin{aligned}h \bigg( g\Big(f(x)\Big) \bigg)&= h \bigg(3x-2\bigg)\\[2ex]&= \sqrt{3x-2} - 3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89fbb7189eaf2dd3c622466c7313806d_l3.png)
複合関数をこれ以上単純化することはできません。したがって、3 つの関数を合成すると、無理関数が生成されます。
![]()