逆余接の導関数

ここでは、逆余接の導関数の公式を示し、関数の逆余接を導出する方法を例とともに説明します。

逆余接微分公式

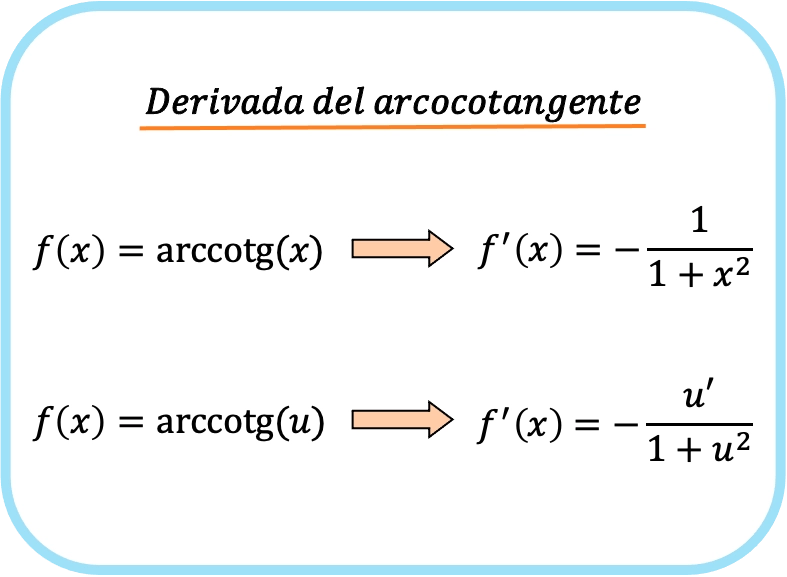
x の逆正接の導関数は、負の 1 を 1 で割った値に x の 2 乗を加えたものです。

$f(x)=\text{arccotg}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{1+x^2}$

したがって、関数の逆正接の微分値は、その関数の微分値を 1 で割った値を引いた値に 2 乗関数を加えた値に等しくなります。

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

最初と 2 番目の式は同じであることに注意してください。唯一の違いは、連鎖ルールが 2 番目の式に適用されることです。実際、u を x に置き換えると、関数 x の導関数は 1 であるため、最初の式が得られます。

逆余接は余接の逆関数ですが、それらの導関数はまったく異なります。実際、関数のコタンジェントを導出するには 3 つの方法があり、それらはすべてここで確認できます。

➤参照: コタンジェントの導関数の公式

逆余接の導関数の公式が何であるかを理解した後、このタイプの三角関数の導関数の 2 つの演習を解いていきます。また、ご質問がある場合は、以下のコメント欄に質問を残していただけます。

この例では、二次関数 x ²の逆余接の微分がどのくらいになるかを確認します。

$f(x)=\text{arccotg}(x^2)$

逆余接の引数には x 以外の関数があるため、連鎖則を使用して逆余接の導関数の公式を適用する必要があります。

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

x を 2 に累乗した導関数は 2x なので、分子に 2x を、分母に引数の 2 乗の関数を入力する必要があります。

$f(x)=\text{arccotg}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{1+(\left(x^2\right)^2}=-\cfrac{2x}{1+x^4}$

この 2 番目の例では、3 次多項式関数の逆余接を導出します。

$f(x)=\text{arccotg}(x^3-9x+2)$

逆余接導関数ルールを使用して導出を行います。

$f(x)=\text{arccotg}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{1+u^2}$

したがって、関数の逆余接の導関数は次のようになります。

$f(x)=\text{arccotg}(x^3-9x+2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{3x^2-9}{1+(x^3-9x+2)^2}$