このページでは、複素行列、共役行列、共役転置行列とは何かを説明します。現在、これらはよく似ていますが、ページの最後までにそれぞれの違いが完全に理解できることがわかります。さらに、各タイプの例とそのプロパティも見ていきます。
複素行列
共役行列と転置共役行列の説明を見る前に、複素行列の概念を確認してみましょう。
複素行列とは何ですか?
複素行列とは、要素間に特定の複素数を持つ行列です。
複素数または虚数は、文字 i で示される実数部と虚数部で構成される数であることを思い出してください。例えば:
![]()
。
複素行列の例
複雑な多次元配列の例をいくつか見てみましょう。
2×2次の複素行列の例
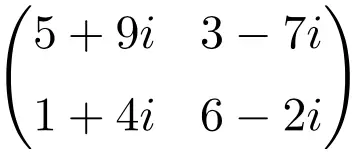
3×3 次元の複素行列の例
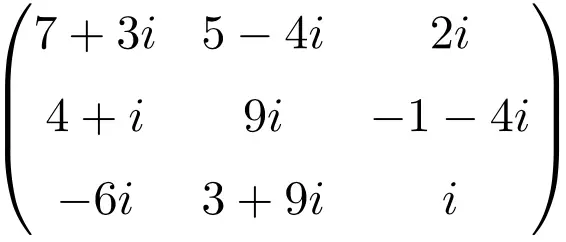
サイズ 4×4 の複素行列の例
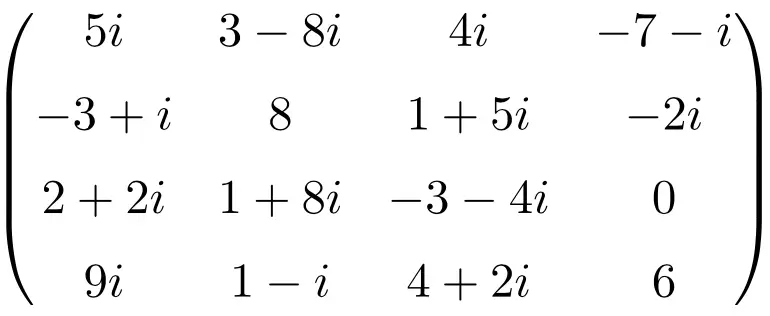
共役行列
複素行列の定義が何であるかを理解したら、共役行列と転置共役行列が何であるかを見てみましょう。
共役行列とは何ですか?
共役行列は、すべての要素が共役に置き換えられた複素行列です。つまり、すべての複素数の虚数部の符号が変更されました。
の共役行列
![]()
は上の水平バーで表されます。
![]()
。
共役行列の例
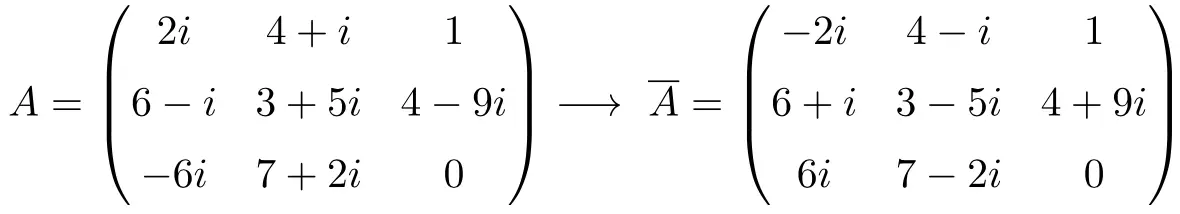
共役行列のプロパティ
このタイプのマトリックスの特徴は次のとおりです。
- 共役行列の共役は元の行列です。
![]()
- 2 つの行列を加算 (または減算) し、その結果を共役させることは、最初に 2 つの行列を別々に共役させてからそれらを加算 (または減算) することと同じです。
![]()
- 2 つの行列の共役積は、 2 つの行列を個別に共役してから行列の乗算を計算することと同じです。
![]()
- 行列にスカラーを乗算し、その結果を共役させることは、最初にスカラーと行列の共役を計算してから積を解くことと同じです。
![]()
- 行列を転置してから共役にするということは、まず行列を共役にしてから転置することを意味します。
![]()
- 行列の逆を実行してからそれを共役にすることは、行列を共役にしてからそれを反転することと同じです。
![]()
- 共役行列のランクは、同じ非共役行列のランクと同じです。
![]()
- 共役行列のトレースを計算することも、共役なしで同じ行列のトレースを計算してからその結果を共役することも関係ありません。
![]()
- 最後に、共役行列の行列式を取得すると、共役を行わずに同じ行列の行列式の結果の共役を計算することになります。
![]()
共役転置行列
最後に、行列を共役する方法を確認した後、共役転置行列の概念に移りましょう。
共役転置(または転置)行列とは何ですか?
転置された (または転置された) 共役行列は、行列を転置し、その共役を作成した後に得られる行列です。
このタイプの行列は、随伴行列または単に随伴行列とも呼ばれます。さらに、通常はアスタリスクで表されます。
![]()
と描く数学者もいますが、
![]()
どちらか
![]()
。
共役転置行列の例
以下は、行列の転置 (または共役転置) を計算する例です。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix}1+3i&2-i & -4i \\[1.1ex] 6 & 8+2i & 3-5i \\[1.1ex] 7i & 1+9i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d4fc37df446a4600709c54e8b1b78072_l3.png)
まず行列 A を転置します。
![Rendered by QuickLaTeX.com \displaystyle A^t=\begin{pmatrix}1+3i& 6 & 7i \\[1.1ex] 2-i & 8+2i & 1+9i \\[1.1ex] -4i & 3-5i & -2+i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fdc97bb655f8e2f18abbc2e6d480c02b_l3.png)
次に、転置の共役行列を計算します。つまり、すべての複素数の虚数部の符号を変更します。
![Rendered by QuickLaTeX.com \displaystyle A^*=\overline{A^t}=\begin{pmatrix}1-3i& 6 & -7i \\[1.1ex] 2+i & 8-2i & 1-9i \\[1.1ex] 4i & 3+5i & -2-i\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-209bcf07d842e6157663ddc03909d544_l3.png)
したがって、共役転置行列の計算の概要は次のようになります。
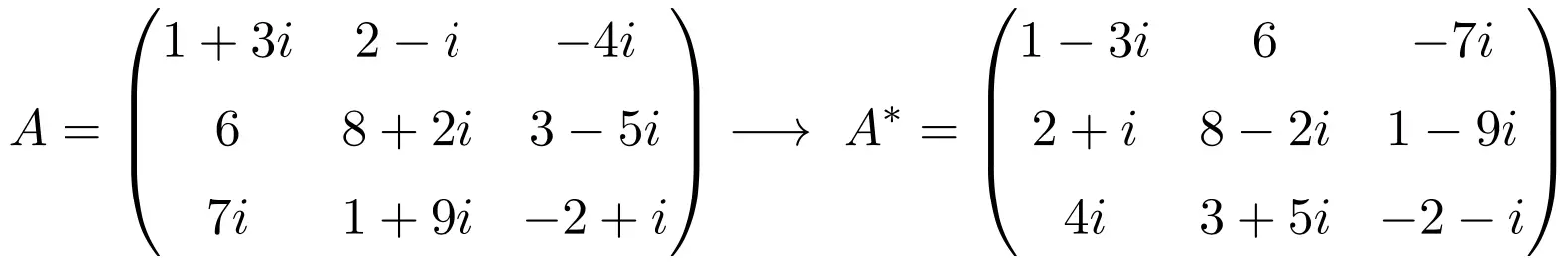
共役転置行列のプロパティ
このタイプの正方行列のプロパティは次のとおりです。
- 以前に転置および共役した行列の共役転置行列が元の行列です。
![]()
- 共役転置行列の加算特性は、2 つの行列を加算 (または減算) してその結果にこの演算を適用することは、最初に各行列の共役転置を実行してからその結果を加算 (または減算) することと同等であることを示しています。
![]()
- 2 つの行列を乗算して共役転置を行うと、共役転置行列の逆積と同じ結果が得られます。
![]()
- スカラーと行列の積の共役転置行列を計算することは、複素数を共役し、行列の共役転置を個別に求めて乗算することと同じです。
![]()
- 行列が反転可能な場合、行列の反転と共役転置演算が実行される順序は無関係です。
![]()