このページでは、行列を加算および減算する方法を説明します。また、完全に理解するのに役立つ例と、練習できるように解決された演習も用意されています。行列加算のすべてのプロパティも見つかります。
行列を加算および減算するにはどうすればよいですか?
2 つの行列の加算 (または減算) を計算するには、行列内の同じ位置を占める要素を加算 (または減算) する必要があります。
例:

2 つの行列を加算または減算するには、それらの行列の次元が同じである必要があることに注意してください。たとえば、次の行列は、最初の行列が 2×2 行列で 2 番目の行列が 3×2 行列であるため、追加できません。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 0 & 2 \end{pmatrix} + \begin{pmatrix} 5 & 6 \\[1.1ex] -2 & 4 \\[1.1ex] 7 & 1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}}](https://mathority.org/wp-content/ql-cache/quicklatex.com-082c648e15685c4ddeac2cc2da502d96_l3.png)
行列の加算と減算の演習問題を解決しました。
演習 1
次の 2×2 行列の合計を計算します。
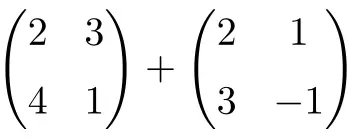
これは、次元 2×2 の 2 つの正方行列の合計です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 3 \\[1.1ex] 4 & 1 \end{pmatrix} + \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} = \begin{pmatrix} 2+2 & 3+1 \\[1.1ex] 4+3 & 1+(-1) \end{pmatrix} = \begin{pmatrix} \bm{4} & \bm{4} \\[1.1ex] \bm{7} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1d9428ad89a6bd149d5e63bc500879ac_l3.png)
演習 2
次の行列減算を実行します。
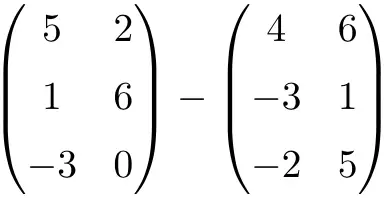
これは、次元 3×2 の 2 つの行列の減算です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 2 \\[1.1ex] 1 & 6 \\[1.1ex] -3 & 0 \end{pmatrix} - \begin{pmatrix} 4 & 6 \\[1.1ex] -3 & 1 \\[1.1ex]-2 & 5 \end{pmatrix} = \begin{pmatrix} 5-4 & 2-6 \\[1.1ex] 1-(-3) & 6-1 \\[1.1ex] -3-(-2) & 0-5 \end{pmatrix} = \begin{pmatrix} \bm{1}& \bm{-4} \\[1.1ex] \bm{4} & \bm{5} \\[1.1ex] \bm{-1} & \bm{-5} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c371e1f01df59f4b8abb018e476e66d7_l3.png)
演習 3
次の次元 3×3 の行列の合計の結果を求めます。
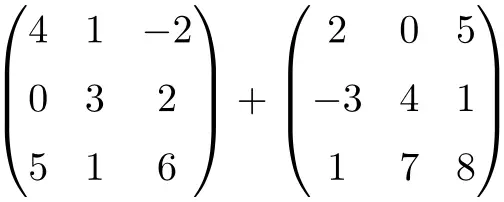
これは、次数 3×3 の 2 つの正方行列の合計です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -2 \\[1.1ex] 0 & 3 & 2 \\[1.1ex] 5 & 1 & 6 \end{pmatrix} + \begin{pmatrix} 2 & 0 & 5 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 1 & 7 & 8 \end{pmatrix} = \begin{pmatrix} 4+2 & 1+0 & -2+5 \\[1.1ex] 0+(-3) & 3+4 & 2+1 \\[1.1ex] 5+1 & 1+7 & 6+8 \end{pmatrix} = \begin{pmatrix} \bm{6}& \bm{1} & \bm{3} \\[1.1ex] \bm{-3} & \bm{7} & \bm{3} \\[1.1ex] \bm{6} & \bm{8} & \bm{14} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-280299cb0b37e1a585466c4570439ec4_l3.png)
演習 4
次の 2 次正方行列の加算と減算を計算します。
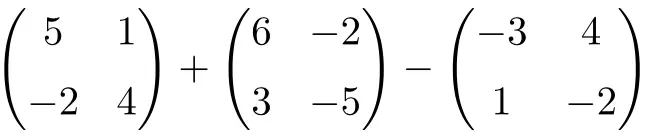
これは、次数 2 の正方行列の加算と減算を組み合わせた演算です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 4 \end{pmatrix} + \begin{pmatrix} 6 & -2 \\[1.1ex] 3 & -5 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c9fa4dba7699c0035ce5081756b4f62e_l3.png)
したがって、最初に左側の行列を追加します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 11 & -1 \\[1.1ex] 1 & -1 \end{pmatrix} -\begin{pmatrix} -3 & 4 \\[1.1ex] 1 & -2 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e1544e4da9d5ad2ea3ec2e4ad0326023_l3.png)
次に、行列の減算を計算します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{14} & \bm{-5} \\[1.1ex] \bm{0} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bd7f32fc7c9429fdfc3b5b745e85975c_l3.png)
演習 5
次の行列の加算と減算を解きます。
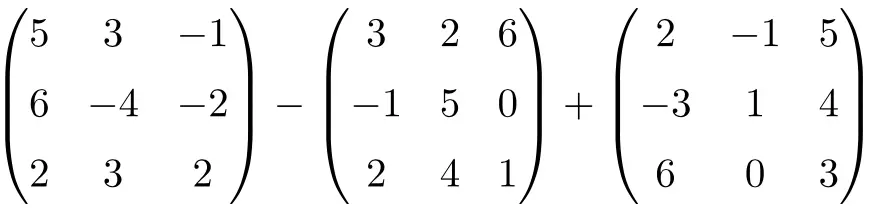
これは、次数 3 の正方行列の減算と加算を組み合わせた演算です。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}5 & 3 & -1 \\[1.1ex] 6 & -4 & -2 \\[1.1ex] 2 & 3 & 2 \end{pmatrix}-\begin{pmatrix} 3 & 2 & 6 \\[1.1ex]-1 & 5 & 0 \\[1.1ex] 2 & 4 & 1 \end{pmatrix} + \begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae66268adcd61258654056815542cf58_l3.png)
まず、行列の減算を解きます。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix}2 & 1 & -7 \\[1.1ex] 7 & -9 & -2 \\[1.1ex] 0 & -1 & 1 \end{pmatrix}+\begin{pmatrix}2 & -1 & 5 \\[1.1ex] -3 & 1 & 4 \\[1.1ex] 6 & 0 & 3 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4401b28babce2beaaa6f840c4ed8c959_l3.png)
そして最後に行列を追加します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} \bm{4} & \bm{0} & \bm{-2} \\[1.1ex] \bm{4} & \bm{-8} & \bm{2} \\[1.1ex] \bm{6} & \bm{-1} & \bm{4} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ffba1ade3d98c434960b54fc0c7ffe1f_l3.png)
行列の加算と減算の方法がわかったので、今度は行列演算の中で最も重要である行列の乗算の方法を見てみましょう。また、このサイトのすべてのページと同様に、練習できるようにステップバイステップの行列乗算の演習も提供されます。 😉
行列プロパティの追加
行列加算には次の特徴があります。
- 行列の加算には可換性の性質があります。
![]()
したがって、行列を追加する順序は同じです。これを実証するために、順序を変更して 2 つの行列を追加します。結果がどのように同じになるかがわかります。
したがって、2 つの行列を特定の順序で追加していきます。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix} + \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7eb454436dc3268ae8d6d2b62f395a7_l3.png)
行列の加算順序を逆にしても、結果は同じままであることに注意してください。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 \\[1.1ex] 5 & 2 \end{pmatrix} + \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -1 \end{pmatrix}= \begin{pmatrix} \bm{5} & \bm{4} \\[1.1ex] \bm{7} & \bm{1} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c1e9cd77bc490913ed30ff63815da355_l3.png)
- 行列加算のもう 1 つの特性は、反対の要素の特性です。
![]()
言い換えれば、行列と同じ行列を加算し、そのすべての要素の符号を変更すると、結果はゼロ行列になります。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 4 & 1 & -3 \\[1.1ex] 2 & 0 & 9 \end{pmatrix} + \begin{pmatrix} -4 & -1 & 3 \\[1.1ex] -2 & 0 & -9 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{0} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-add832e83fe554143cbd4c710315c1c0_l3.png)
- 行列の加算には、次のような中立要素のプロパティもあります。
![]()
この特性は最も明らかであり、任意の行列とゼロでいっぱいの行列が同じ行列と同等であるという事実を指します。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -3 & 4 & 9 \\[1.1ex] 1 & 12 & 6 \end{pmatrix} + \begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{1} & \bm{5} \\[1.1ex] \bm{-3} & \bm{4} & \bm{9} \\[1.1ex] \bm{1} & \bm{12} & \bm{6} \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac7b0ba246075c196188798be2c6a034_l3.png)
- 行列の加算には結合特性があります。
![]()
したがって、行列を追加する順序は同じです。次の例を見てください。異なる順序で 3 つの行列を追加しても、結果は同じです。
![Rendered by QuickLaTeX.com \displaystyle A = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} \qquad B = \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \qquad C = \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-bae8e10bca43351f3a84f83bfe50ab55_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\left( A + B \right) + C & =\left( \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} \right) + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & = \begin{pmatrix} 6 \\[1.1ex] 0 \end{pmatrix} + \begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{9} \\[1.1ex] \bm{0} \end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2cc2b7a14cacc7e403cd729cd863d309_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} A + \left( B + C \right) & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \left( \begin{pmatrix} 4 \\[1.1ex] -1 \end{pmatrix} +\begin{pmatrix} 3 \\[1.1ex] 0 \end{pmatrix} \right) \\[2ex] & = \begin{pmatrix} 2 \\[1.1ex] 1 \end{pmatrix} + \begin{pmatrix} 7 \\[1.1ex] -1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{9} \\[1.1ex] \bm{0}\end{pmatrix} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab1f88e74b139451eccb0471988c3db_l3.png)