線形回帰は、2 つの連続変数間の関係を研究するために使用される統計手法です。線形回帰の主な考え方は、データに最もよく適合する直線を見つけることです。さらに、ある変数の値を別の変数の値に基づいて予測することもできます。
この直線は「回帰」と呼ばれ、未知の値を予測したり、変数間の関係を理解したりするために使用されます。要約すると、線形回帰は 2 つの連続変数間の関係を分析およびモデル化するためのツールです。
線形回帰が重要なのはなぜですか?
線形回帰が重要なのは、2 つの連続変数間の関係をモデル化して分析できるため、将来の値を予測したり、データのパターンや傾向を特定したりするのに役立ちます。
さらに、線形回帰は、統計、および経済学、心理学、医学、工学、物理学などの科学研究および社会研究のほとんどの分野における基本的なツールです。業界やビジネスにおけるビジネス上の意思決定やプロセスの最適化にも使用されます。
要約すると、線形回帰は、研究や実践のさまざまな分野でデータと変数間の関係を分析し、より深く理解できるようにする強力で多用途のツールです。
線形回帰にはどのような種類がありますか?
線形回帰にはいくつかの種類があり、そのうちのいくつかは次のとおりです。
単純な線形回帰
単線形回帰分析は、単一の従属変数に対する独立変数の影響を研究するために広く使用されているツールであり、それらの間に線形関係があると考えられます。単純な線形回帰式を使用すると、独立変数の値に基づいて従属変数の値を推定できます。
単純な線形回帰式は次のとおりです。
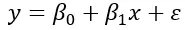
ここで、β 0は独立変数がゼロの場合の従属変数の値です。 β 1 は独立変数の単位変化当たりの従属変数の変化を表し、εは残差または誤差を表す。つまり、式の線形関係では説明できないデータの変動性です。
多重線形回帰
多重線形回帰は、調査対象の従属変数に影響を与える可能性のある独立変数が複数ある場合に使用されます。
重回帰の式は次のとおりです。
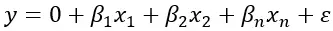
Y は従属変数を表し、 β 1 、β 2 、β nは Y の値に影響を与える可能性のある独立変数、回帰、ε は存在する可能性のある誤差を表します。この式により、独立変数の値に基づいて Y の値を推定することができます。
線形回帰式とは何ですか?
線形回帰式は次のとおりです。
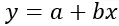
金:
y は、予測される従属変数 (または応答) です。
x は、予測を行うために使用される独立 (または予測) 変数です。
a は切片 (または、x=0 の場合に回帰直線が Y 軸と交差する点) です。
b は回帰直線の傾きです (x の各変化に対する y の変化率を示します)
a と b の値を見つけるには、観測値と回帰直線によって予測される値の間の二乗誤差の合計を最小化する最小二乗法を使用します。
式は次のとおりです。
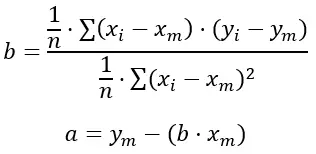
金:
n は、持っているデータセットの総数です。
x iと y iは、合計で取得する値です。
x mと y mは各変数の平均値です。
線形回帰法を適用するにはどうすればよいですか?
線形回帰法は、以下の手順に従って適用できます。
- データを収集する: 最初に行うことは、興味のあるデータを収集することです。たとえば、あるグループの給与と年齢の関係を研究したい場合は、各人の給与と年齢に関する情報を収集する必要があります。
- データをプロットする– 次に、独立変数 (この場合は年齢) が横軸に配置され、従属変数 (給与) が縦軸に配置されるデカルト平面上にデータをプロットする必要があります。
- 回帰直線を決定する: データに最もよく適合する回帰直線を決定する必要があります。この直線は、サンプル統計データを使用して計算された線形回帰式から得られます。
- 適合度の評価– 回帰直線がデータにどの程度適合しているかを評価することが重要です。これは統計的測定を使用して行うことができます。
- 予測を行う– 最後に、結果の回帰直線を使用して予測を行うことができます。たとえば、30 歳の人の給与を予測する場合は、線形回帰式を使用し、それに年齢の値を代入します。
これらの手順は、使用する線形回帰の種類と使用する統計ソフトウェアに応じて若干異なる場合があることに注意することが重要です。
線形回帰は何に使用されますか?
線形回帰は、1 つの変数が別の変数の値に影響を与える可能性がある2 つの変数間の関係を分析する場合に使用されます。したがって、線形回帰を使用すると、独立変数が従属変数にどのような影響を与えるかを理解し、独立変数に基づいて従属変数の値を予測できます。
線形回帰では、2 つの変数間の関係が線形であると仮定していることに注意することが重要です。これは、従属変数の変化が独立変数の変化に比例することを意味します。
したがって、2 つの変数間の線形関係が疑われる場合は、線形回帰を使用する必要があります。この条件が満たされない場合は、他の非線形回帰モデルまたは別の統計手法を使用する方が適切な場合があります。
線形回帰の応用にはどのようなものがありますか?
線形回帰は、統計、経済学、工学、社会科学、生物学などの分野の幅広いアプリケーションで使用されます。線形回帰の最も一般的な応用例をいくつか示します。
- 傾向分析– 過去のデータの傾向を分析し、将来の傾向を予測します。
- 予測– 1 つ以上の変数の過去の値に基づいて、変数の将来の値を予測します。
- 市場調査: 製品の需要とその価格の関係を研究すること。
- 財務分析– 企業の収益と支出の関係を調査し、将来の財務結果を予測します。
- 疫学研究: 危険因子への曝露と病気の発症確率との関係を研究します。
- 社会科学– 心理学、社会学、政治学などの分野で 2 つ以上の変数間の関係を研究します。
- オペレーションズ リサーチ– 線形回帰は、産業工学や物流などの分野で複雑なシステムをモデル化し、最適化するために使用されます。
- 環境科学– 環境要因と生態系への影響との関係を研究するために使用されます。
線形回帰の残差とは何ですか?
線形回帰の残差は、従属変数の観測値と線形回帰モデルによって予測された値との差です。言い換えれば、実際のデータ点と回帰直線の間の垂直距離です。
残差の背後にある考え方は、回帰直線がデータによく適合する場合、残差は小さくランダムになるはずであるということです。残差が大きい場合、または特定のパターンに従っている場合は、変数間の関係が線形でないこと、または線形回帰モデルがデータに適合していないことを示している可能性があります。
残差は、線形回帰モデルの精度を評価し、モデルの品質に影響を与える可能性のある外れ値や影響力のあるデータ ポイントを特定するためにも使用されます。
複数の従属変数を使用して線形回帰を実行できますか?
線形回帰では、従属変数は常に単一変数です。ただし、複数の独立変数を持つことができます。この場合、多重線形回帰について話します。
重線形回帰の目的は、単一の従属変数に対する複数の独立変数の影響を研究することです。
線形回帰の係数をどのように解釈できますか?
線形回帰では、係数は回帰直線の傾きと切片を表します。傾きは独立変数の単位変化当たりの従属変数の変化を示し、切片は独立変数がゼロに等しいときの従属変数の値を表します。
線形回帰の数値例
簡単な例は次のとおりです。
あるグループの年齢と身長の次のデータがあるとします。
| 歳) | 身長(cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| 四五 | 190 |
私たちは、これらの人々の年齢と身長の間に関係があるかどうかを判断したいと考えています。これを行うには、線形回帰を使用します。
まず、データを使用して統計グラフを描画できます (この場合、散布図の使用をお勧めします)。
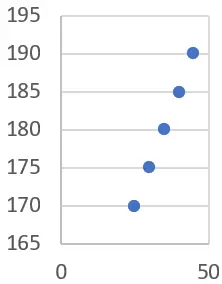
年齢が上がるにつれて身長も伸びるという明らかな傾向があることがわかります。これは、線形回帰直線を計算することで確認できます。
前に見た式を使用して線形回帰直線の係数を計算すると、次が得られます。
= 145 で
b = 1
したがって、線形回帰直線の方程式は次のようになります。
身長 = 145 + 1 年齢
この方程式を使用して、年齢に基づいて人の身長を予測できます。たとえば、ある人が 32 歳の場合、身長は次のようになると予測できます。
身長 = 145 + 1 32 = 177 cm