このページでは、線と円の間に存在するさまざまな相対位置について説明します。さらに、線と円の間の相対位置を見つける方法もわかります。
線と円の相対的な位置は何ですか?
解析幾何学では、円に対する線の相対位置は、外部、接線、または割線のみとなります。
- 外側: 線と円の中心の間の距離が半径より大きい場合。
- 接線: 線と円の中心の間の距離が半径と等しい場合。
- セカント: 線と円の中心の間の距離が半径より小さい場合。
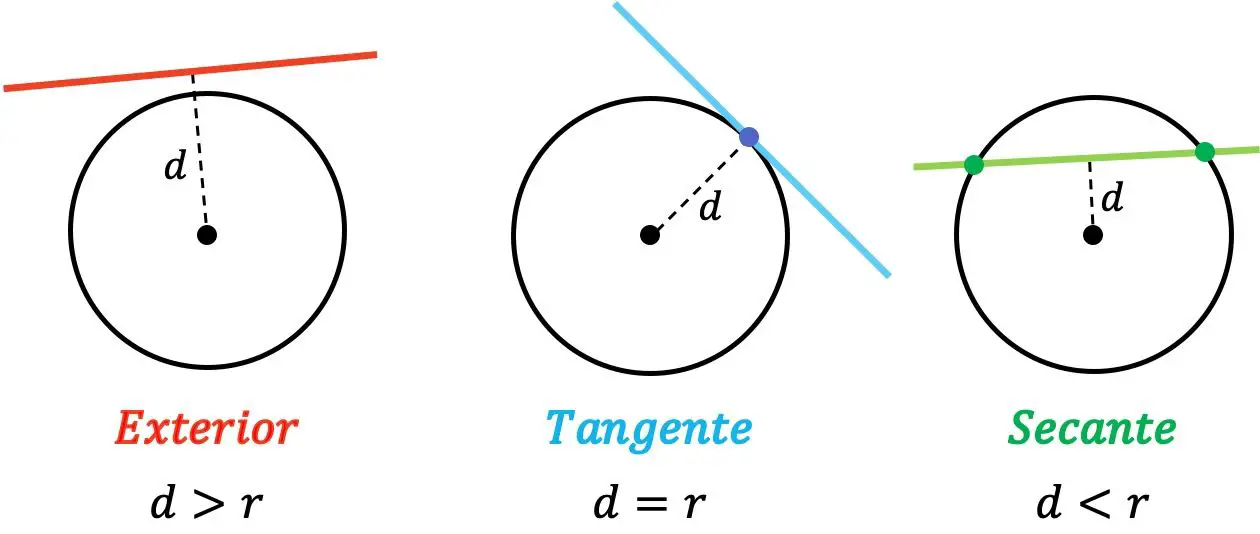
したがって、線が円の外側にある場合、その線はどの点でも円と交差しません。一方、線が円に接する場合、両者には共通点があります。そして最後に、線が 2 つの異なる点で円と交差すると、線は円に割られます。
線と円の間の相対位置を決定するにはどうすればよいですか?
平面内の円に対する線の相対位置を見つける方法は 2 つあります。1 つは線と円の中心の間の距離を計算する方法で、もう 1 つは次の方程式の複合連立方程式を解くことです。直線と円の方程式。
次に、それぞれのメソッドがどのようなものかを正確に見ていきます。
方法 1: 線と円の中心の間の距離
線と円の相対位置の概念の説明で見たように、線と円の中心との距離は、それがどのような相対位置であるかを示します。
したがって、この方法は、線と円の中心の間の距離を見つけることから構成されます。明らかに、それを行うには、点と線の間の距離を計算する方法を知っている必要があります。このページでは、その方法、例、および練習するための解決された演習を確認できます。
したがって、取得された距離の結果に応じて、次のような場合になります。
- 取得した距離が円の半径より大きい場合、線は円の外側になります。
- 得られた距離が円の半径と等しい場合、線は円に接します。
- 取得した距離が円の半径より小さい場合、線は円と交差します。
方法 2: 連立方程式を解く
円に対する線の相対位置を見つけるもう 1 つの方法は、線の方程式と円の方程式で形成される連立方程式を使用することです。明らかに、この方法を適用するには、 円周の方程式が何であるか、および直線の方程式の公式が何であるかを知る必要があります。
方程式系の解の数に応じて、次のような場合に直面することになります。
- 連立方程式に解がない場合は、直線と円に共通点がなく、直線が円の外側にあることを意味します。
- 連立方程式の解が 1 つである場合、これは直線と円が共通点を持ち、したがって直線が円に接することを意味します。
- 連立方程式に 2 つの解がある場合、これは直線と円に 2 つの共通点があることを意味するため、直線は円に割られます。