線の傾き (公式) - マソリティ

このページでは、線の傾きについて最も詳しく説明します。公式、計算例、線の傾きの概念の意味など。また、傾きを簡単に識別する方法もわかります。方程式から直線を求めることができ、さらに、段階的に解く演習で練習することができます。

線の傾きを求める公式

線の傾きは、 2 点間の垂直変位をこれらの同じ 2 点間の水平変位で割った値に等しくなります。

つまり、直線上に 2 つの点があるとします。

$P_1(x_1,y_1) \qquad P_2(x_2,y_2)$

線の傾きの公式は次のとおりです。

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

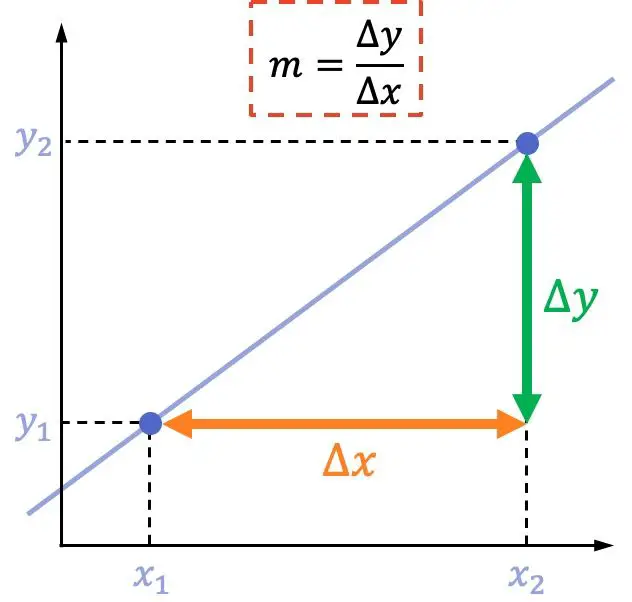
2 点から直線の傾きを計算する例

次に、次の式を使用して線の傾きを計算する例を見てみましょう。

次の 2 点を通る直線の傾きを計算します。

$P_1(3,1) \qquad P_2(5,7)$

この線の傾きを求めるには、次の公式を適用するだけです。

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}$

したがって、線の傾きは 3 に等しくなります。

方程式から直線の傾きを求める

上のセクションでは、線の傾きを数値的に決定する方法について説明しました。ただし、必ずしも計算する必要はなく、直線の方程式からその値を特定することもできます。方程式のタイプはそれぞれ異なるため、それぞれのケースを個別に分析します。

直線の方程式を明示的に指定した場合の傾き

直線の明示的な方程式は次の式に従います。

$y =\color{blue}\bm{m}\color{black}x+n$

次にパラメータ

$m$

線の傾きに相当します。

直線の点と傾き方程式から与えられた傾き

直線の点と傾きの方程式の式は次のとおりです。

$y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)$

先ほどと同様に、係数は

$m$

線の傾きに相当します。

直線の陰的な方程式を考慮した傾き

直線の暗黙的な方程式 (一般方程式またはデカルト方程式とも呼ばれます) が与えられると、次のようになります。

$Ax+By+C=0$

線の傾きは次のようにして求めることができます。

$m=-\cfrac{A}{B}$

線の方向ベクトルを考慮した傾き

線の方向ベクトルは、その方向を示すベクトルです。したがって、線の方向ベクトルが次の場合、

$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

この線の傾きは次のとおりです。

$m=\cfrac{\text{v}_2}{\text{v}_1}$

角度を指定した傾斜

最後に、線が角度を形成する場合は、

$\alpha$

横軸 (X 軸) の正の部分では、その傾きは角度の正接に等しくなります。

$m = \text{tg}(\alpha)$

線の傾きの意味

上記のすべての情報により、線の傾きを見つける方法はすでに完全にわかっています。しかし実際には…線の傾きは何を意味するのでしょうか?

線の傾きは、グラフの水平単位ごとに線が上昇する垂直単位を示します。

たとえば、次の線の表現では、傾きが 2 に等しいため、水平単位ごとに垂直方向に 2 単位進むことがわかります。

さらに、線の傾きもその急峻さを示します。

線が増加している (上昇している) 場合、その傾きは正です。
線が減少 (下降) している場合、その傾きは負になります。
線が完全に水平の場合、その傾きは 0 に等しくなります。
線が完全に垂直の場合、その傾きは無限大に等しくなります。

線の相対位置

一方、2 つの直線間の相対位置は、傾きの特性から知ることもできます。

2 つの線の傾きが異なる場合、これはそれらが交差する、つまり点で交差することを意味します。

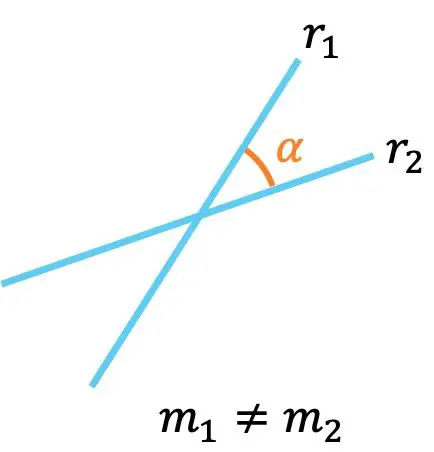
さらに、傾斜を横切る 2 本の線の間の角度は、次の式で計算できます。

$\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}$

次に、2 つの直線の傾きが同じ場合、これはそれらが平行であることを意味します。

最後に、2 本の垂直または直交する線 (90 度を形成する) の傾きは次の条件を満たします。

これは 2 つの線が互いに平行か垂直かを調べる 1 つの方法ですが、他の方法もあり、さらに高速な方法もあります。さらに詳しく知りたい場合は、線間の直角度と平行度の説明を参照してください。さらに、これらのページでは、別の線に垂直 (または平行) な線を見つける方法も説明します。

線の傾きの問題を解決しました

演習 1

次の 2 点を通る直線の傾きを求めます。

$P_1(5,6) \qquad P_2(8,3)$

解決策を参照

線の傾きを計算するには、次の式を使用する必要があります。

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}$

演習 2

次の 2 点を通る直線の傾きを計算します。

$P_1(-3,1) \qquad P_2(-2,-4)$

解決策を参照

線の傾きを見つけるには、次の公式を使用する必要があります。

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}$

演習 3

それぞれの線の傾きはどれくらいでしょうか?

$\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}$

解決策を参照

A)この直線は陰的な方程式として表現されるため、その傾きは 2 (

$x$

）。

B)直線は点と傾きの方程式によって定義されるため、その傾きは 4 (括弧の前の数字) になります。

C)この直線は暗黙的な方程式形式であるため、その傾きは次のようになります。

$m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}$

D)直線はパラメトリック方程式の形式で定義されているため、最初にその方向ベクトルを見つける必要があり、それを使用して直線の傾きを計算できます。したがって、方向ベクトルの成分は係数に付随する項です。

$t:$

$\vv{\text{v}} = (-1,2)$

そして、線の方向ベクトルがわかれば、線の傾きを決定できます。

$m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}$

演習 4

各グラフ線の傾きを決定します。

解決策を参照

青右

青い線は X ごとに Y が 1 ずつ増加するため、その傾きは 1 に等しくなります。

$m=1$

右の緑

緑の線は X ごとに Y が 3 ずつ増加するため、その傾きは 3 になります。

$m=3$

レッドライン

赤い線は X ごとに 2 Y ずつ減少するため、その傾きは -2 に等しくなります。

$m=-2$

線の傾き（公式）

線の傾きを求める公式

2 点から直線の傾きを計算する例