このページでは、線と平面の相対的な位置がわかります。直線と平面の間の相対位置を計算する方法 (2 つの方法) を説明し、さらに、例題と演習を段階的に解くことができます。
線と平面の相対位置は何ですか?
線と面の間で考えられるすべての相対位置を調べる前に、線とは何か、面とは何かを知る必要があることは明らかです。したがって、これら 2 つの概念がまだよくわからない場合は、まずリンク先のページで詳しく説明されているページを参照することをお勧めします。
したがって、解析幾何学では、線と平面の間の空間内の相対位置は 3 つだけです。
- 平面に含まれる線: 線が平面に含まれる場合、これはそれらに無限の数の共通点があることを意味します。
- 平行な線と平面: 線と平面は、共通点がない場合に平行です。
- 線と平面の交差: 線と平面が点で交差する場合、線と平面は交差します。したがって、彼らの共通点は1つだけです。
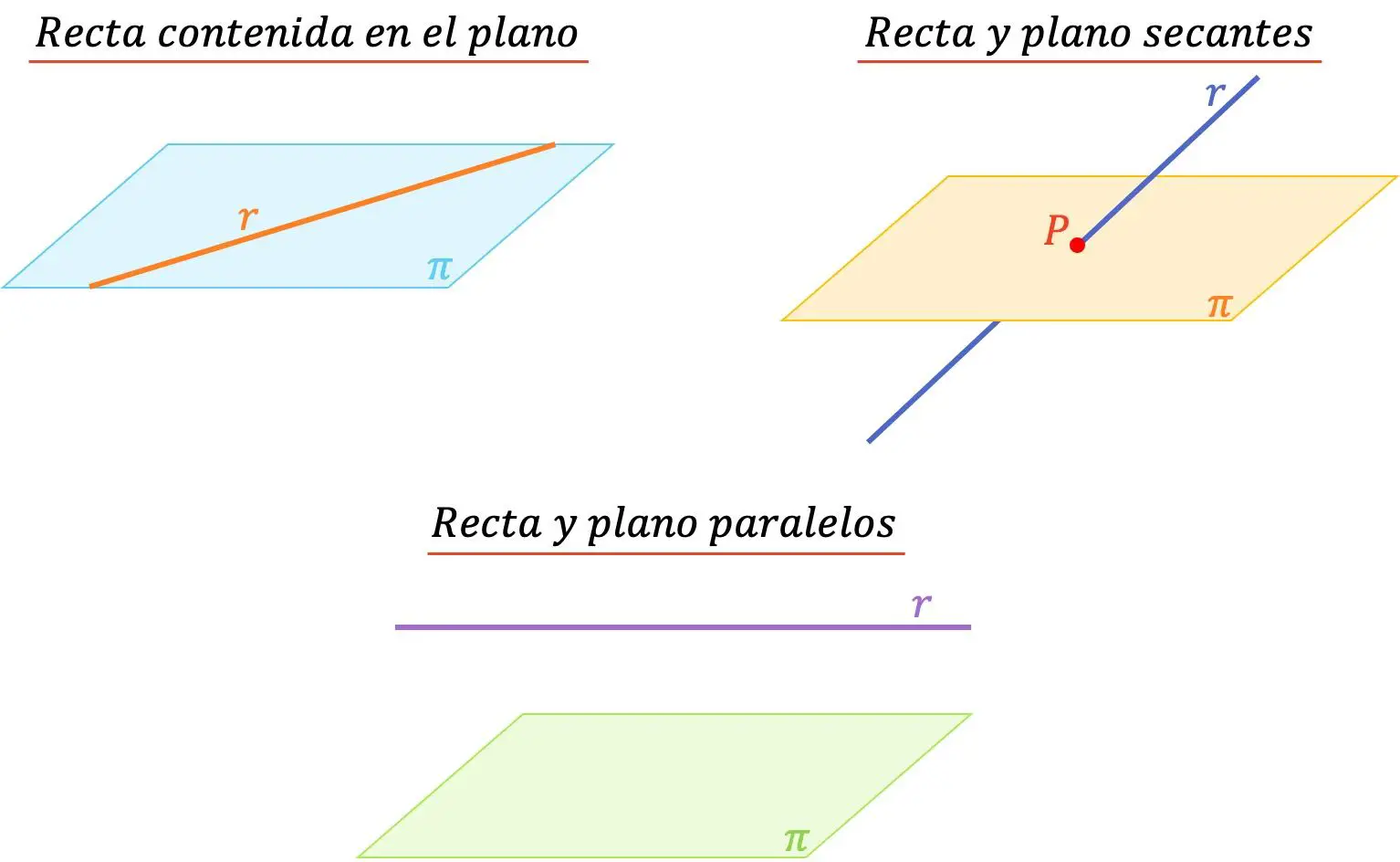
一方、線が平面内に含まれる場合、または線と線が平行である場合、線と線のなす角度は 0°になります。一方、線と平面が交差する場合、2 つの幾何学的要素間の角度は 0 度 (含まれない) から 90 度 (両端の値を含む) の範囲になります。
直線と平面の相対位置を計算するにはどうすればよいですか?
空間内の線と平面の間の相対位置を見つけるには、主に範囲による方法とベクトルによる方法の 2 つがあります。
直線が陰的な (または一般的な) 方程式として表現される場合、ランク法を使用する方が簡単です。一方、直線が別のタイプの方程式で与えられる場合、たとえば線がベクトル、パラメトリック方程式、または連続方程式の形式である場合は、ベクトル法を使用する方が高速です。
直線の方程式がどのようなものかを覚えていない場合は、 直線の方程式をすべて参照できるページを用意しておきます。ここでは、すべての直線の方程式、2 点を通る直線の方程式を素早く求める公式、段階的に解決される例題と演習が見つかります。
したがって、問題に応じていずれかの方法を使用する方が現実的です。そのため、両方の手順の実行方法を知っておくことをお勧めします。以下に両方の方法を例を挙げて説明します。
直線が暗黙的な (または一般的な) 方程式の形式である場合
線と平面の間の相対位置を決定する 1 つの方法は、2 つの行列のランクを計算することです。
直線がその暗黙的な (または一般的な) 方程式によって定義されている場合:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}A_1x+B_1y+C_1z+D_1=0 \\[2ex] A_2x+B_2y+C_2z+D_2=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-90fc7032d2804ef53ac3136f01ee9d86_l3.png)
そして、計画は一般方程式の形でも表現されます。
![]()
平面と直線の方程式の係数 A、B、C で構成される行列を A と呼びます。
![Rendered by QuickLaTeX.com \displaystyle A =\begin{pmatrix} A_1&B_1&C_1\\[1.1ex] A_2&B_2&C_2\\[1.1ex] A_3&B_3&C_3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-e697e27706489cb97d773b722c84ad37_l3.png)
そして、行列 A’ は、2 つの方程式のすべての係数を含む拡張行列になります。
![Rendered by QuickLaTeX.com \displaystyle A' =\begin{pmatrix} A_1&B_1&C_1&D_1\\[1.1ex] A_2&B_2&C_2&D_2\\[1.1ex] A_3&B_3&C_3&D_3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6c87c6559e077c5bedb08d62e386f0bb_l3.png)
次に、線と平面の間の相対位置は、次の表に従って、前の 2 つの行列の範囲の値によって決定されます。
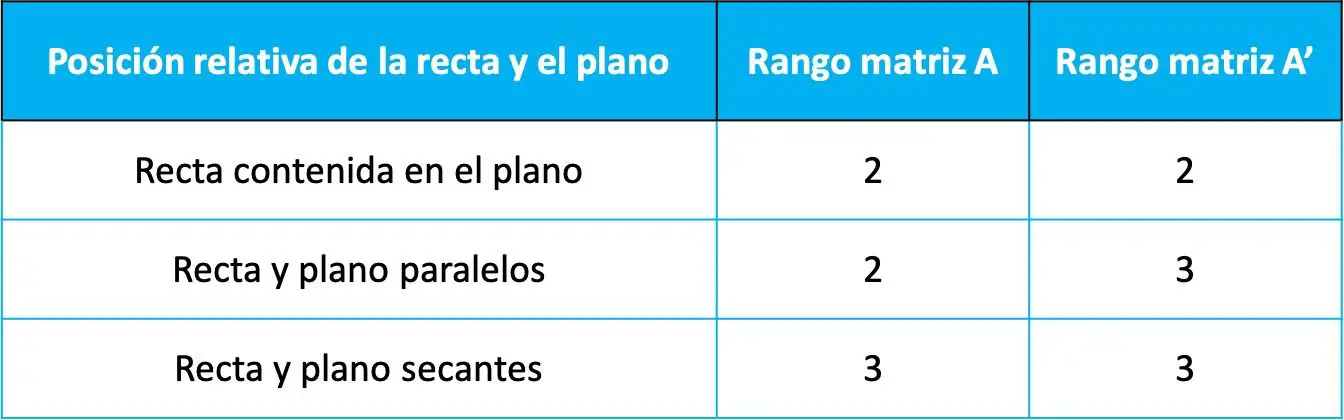
相対位置がこれら 2 つの行列のランクに依存することは、ルーシュ-フロベニウスのトーレム (連立一次方程式を解くために使用される定理) から示すことができます。ただし、このページではデモを行う必要はありません。また、あまり役に立たないため、デモは行いません。
範囲によって直線と平面の相対位置を求める方法の例
これがどのように行われるかを正確に理解できるように、例として演習を解いてみます。
- 次の線と次の平面の間の相対位置を調べます。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}2x+y+z+3=0 \\[2ex] 4x-y+5z+2=0\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-794d91d1740ca80c422936e5e06abefd_l3.png)
![]()
直線は 2 つの交差する平面によって定義され、暗黙的な方程式として表現されます。そこで、ランク法を使って線と平面の相対位置を調べます。
最初に行うことは、次の方程式の係数を使用して行列 A と拡張行列 A’ を構築することです。
![Rendered by QuickLaTeX.com \displaystyle A =\begin{pmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{pmatrix} \qquad \qquad A' =\begin{pmatrix} 2&1&1&3\\[1.1ex] 4&-1&5&2\\[1.1ex] 2&2&0&-6\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-819af000774ddbc89e11df809bcb2a28_l3.png)
次に、各行列のランクを計算する必要があります。まず行列式によって行列 A の範囲を求めます。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&1\\[1.1ex] 4&-1&5\\[1.1ex] 2&2&0\end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-997e4d9c9bd1522795a581d0fb62cfdf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1\\[1.1ex] 4&-1\end{vmatrix} =-6 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-169fab3e064b8bb744ef9cc546bfe201_l3.png)
![]()
行列 A の行列式は 0 ですが、行列式が 0 とは異なる 2×2 部分行列が含まれているため、ランク 2 の行列になります。
一方で、行列 A’ のランクも計算する必要があります。そして、拡張行列 A’ の範囲は常に行列 A の範囲と少なくとも同じになるため、ランク 3 か 2 かを確認するだけで済みます。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix} 2&1&3\\[1.1ex] 4&-1&2\\[1.1ex] 2&2&-6\end{vmatrix} =62 \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-ae375c2cd910e2e52f242facef2aecec_l3.png)
![]()
一方、拡張行列 A’ には 0 とは異なる 3×3 副行列式があるため、ランク 3 になります。
したがって、行列 A はランク 2 であり、行列 A’ はランク 3 であるため、直線と平面は平行になります。
直線が別の種類の方程式の場合
直線が陰的な方程式以外で表現される場合、それがベクトル方程式、パラメトリック方程式、連続方程式であっても、以下に説明する方法を使用することが望ましい。
したがって、直線がベクトル方程式、パラメトリック方程式、または連続方程式の形式で与えられる場合、それはその直線に属する点とその方向ベクトルがわかっていることを意味します。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{v}}_r \\[2ex] P\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a5a0fe0918b9eb196b470ffde6dffb81_l3.png)
一方、平面に対する法線 (または垂直) ベクトルが何かもわかります。
![]()
次に、2 つのベクトルと線の点から、線と平面の間の相対位置を次のように計算できます。
- 線の方向ベクトルと平面に垂直なベクトルの間のスカラー積が 0 以外の場合、これは線が平面に対して割線であることを意味します。
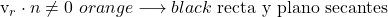
- しかし、線の方向ベクトルと平面に垂直なベクトルの間のスカラー積が 0 に等しい場合、線が平面に含まれているか、線が平行であるかの 2 つの可能性があります。そして、それがどちらの場合であるかを知るには、直線上の点の座標を平面の方程式に代入する必要があります。
- 点が平面の方程式を満たす場合、線は平面に含まれます。
- 一方、点が平面の方程式を満たさない場合、直線と平面は平行になります。
![Rendered by QuickLaTeX.com \left.\begin{array}{c} \vv{\text{v}}_r\cdot \vv{n} = 0\\[2ex]P \in \pi \end{array} \right\} \color{orange}\longrightarrow \color{black}\ \text{recta contenida en el plano}](https://mathority.org/wp-content/ql-cache/quicklatex.com-67bea80768d5723b1a1a79404b6dad60_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{array}{c} \vv{\text{v}}_r\cdot \vv{n} = 0\\[2ex] P \ \cancel{\in} \ \pi \end{array} \right\} \color{orange}\longrightarrow \color{black} \ \text{recta y plano paralelos}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1eccf7b373d59c89e835ae6c64e3d980_l3.png)
ベクトルを使用して直線と平面の相対位置を決定する例
このメソッドの理論を理解したら、今度は演習を段階的に解決してみましょう。
- 次の線と次の平面の間の相対位置を見つけます。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases}x=2-3t \\[1.7ex] y=-1+2t \\[1.7ex] z=-2t\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7df9c39f91ee48f9c11804e81a7cb57a_l3.png)
![]()
まず、直線はパラメトリック方程式として定義されるため、その方向ベクトルとそれが通過する点は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(-3,2,-2) \\[2ex] P(2,-1,0) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c38a901be64fc1a358200bc95c6cafc6_l3.png)
一方、平面に垂直なベクトルは次のようになります。
![]()
線の方向ベクトルと平面に垂直なベクトルがわかったら、その 2 つのスカラー積を計算する必要があります。
![Rendered by QuickLaTeX.com \begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (-3,2,-2) \cdot (2,1,-2) \\[2ex] & = -3 \cdot 2+2 \cdot 1 -2\cdot (-2) \\[2ex] &= -6 +2 +4 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cffc4ca748ea137ce81d1cb185c28b1b_l3.png)
内積の結果はゼロであるため、線は平面内に含まれるか、平面に平行であることのみが可能です。したがって、どちらの場合であるかを調べるために、直線上の点のデカルト座標を平面の方程式に代入します。
![]()
![]()
![]()
直線の点を平面の方程式に代入すると等式が得られます。したがって、点は平面の方程式を尊重し、その結果、直線は平面に含まれます。