このページでは、直交行列とは何か、および直交行列と逆行列との関係について説明します。また、それを完全に理解するためにいくつかの例も表示されます。さらに、直交行列をチェックする公式も教えます。これを使用すると、直交行列をすばやく見つける方法がわかります。最後に、これらの特定の行列の特性と応用、および典型的な解答済みの試験演習が見つかります。
直交行列とは何ですか?
直交行列の定義は次のとおりです。
直交行列は、転置(または転置)を乗じた正方実数行列であり、単位行列と等しくなります。つまり、次の条件が満たされます。
![]()
金
![]()
は直交行列であり、
![]()
はその転置行列を表します。
この条件を満たすには、直交行列の列と行が直交単位ベクトルである必要があります。つまり、正規直交基底を形成している必要があります。このため、一部の数学者はこれらを正規直交行列と呼ぶこともあります。
直交行列の逆行列
直交行列の概念を説明するもう 1 つの方法は、直交行列の転置 (または転置) 行列がその逆行列に等しいため、逆行列を使用することです。
この定理を完全に理解するには、逆行列の方法を知っておくことが重要です。このリンクでは、逆行列とそのすべてのプロパティの詳細な説明が見つかり、さらにステップごとに解決された練習問題も提供されます。
直交行列の逆行列は、直交行列条件と逆行列の主な特性を使用して、その転置と同等であることを簡単に示すことができます。
![Rendered by QuickLaTeX.com \left.\begin{array}{c} A \cdot A^t =I \\[2ex] A \cdot A^{-1} = I\end{array} \right\} \longrightarrow \ A^t=A^{-1}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7666e4730a6311c088c7e8d7f0f38_l3.png)
したがって、直交行列は常に可逆行列、つまり、正規行列または非縮退行列になります。
次に、直交行列の例をいくつか見て、すべての概念を理解します。
2×2直交行列の例
次の行列は 2×2 次元の直交行列です。
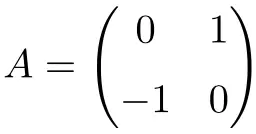
転置による積を計算することで、直交であることを確認できます。
![]()
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t= \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f7baa091c2fd963507b93e6bec5c386b_l3.png)
結果は同一行列となるため、A が直交行列であることを確認します。
3×3直交行列の例
次の行列は 3×3 次元の直交行列です。
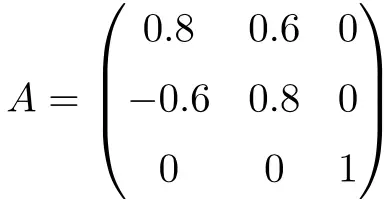
行列 A にその転置を乗算することで、それが直交であることを示すことができます。
![Rendered by QuickLaTeX.com \displaystyle A\cdot A^t = \begin{pmatrix}0.8&0.6&0\\[1.1ex] -0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}\cdot \begin{pmatrix}0.8&-0.6&0\\[1.1ex] 0.6&0.8&0\\[1.1ex] 0&0&1\end{pmatrix}= \begin{pmatrix} 1 & 0 & 0\\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-35687f56ff4ad5d1b19ea673b4ac85de_l3.png)
解はユニタリ行列であるため、A が直交行列であることを示します。
2×2直交行列を求める公式
次に、次数 2 のすべての直交行列が同じパターンに従うという証明を見ていきます。
サイズ 2×2 の一般的な行列を考えてみましょう。
![Rendered by QuickLaTeX.com \displaystyle A=\begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac19d6ab63d390a9340cbce4014b1136_l3.png)
この行列が直交するには、次の行列方程式が満たされる必要があります。
![]()
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} a & b \\[1.1ex] c & d \end{pmatrix} \cdot \begin{pmatrix} a & c \\[1.1ex] b & d \end{pmatrix} =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e108701513ef6f2118e3b7d32657cd8_l3.png)
行列の乗算を解くと、次の方程式が得られます。
![Rendered by QuickLaTeX.com \displaystyle \begin{pmatrix} a^2+b^2 & ac+bd \\[1.1ex] ac+bd & c^2+d^2 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d5435c614cb0da442fe04f65aec89637_l3.png)
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{c}a^2+b^2=1 \\[2ex] ac+bd=0 \\[2ex] c^2+d^2=1 \end{array} \qquad \begin{array}{l} (1) \\[2ex] (2) \\[2ex] (3) \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f8897132ecdbf389450e8c5fa1707226_l3.png)
よく見ると、これらの等式は基本的なピタゴラス三角関係によく似ています。
![]()
その結果、式 (1) および (3) を満たす項が得られます。
![Rendered by QuickLaTeX.com \displaystyle \begin{array}{l} a = \cos \theta \qquad \qquad \qquad c = \sin\phi \\[2ex] b = \sin \theta \qquad \qquad \qquad d = \cos \phi\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9abeb023c5050d8d7f6fbab8c52227ba_l3.png)
さらに、2 番目の方程式に値を代入すると、2 つの角度の関係が得られます。
![]()
![]()
![]()
つまり、次の 2 つの条件のいずれかを満たす必要があります。
![]()
![]()
したがって、結論として、直交行列は次の 2 つの行列のいずれかの構造を持つ必要があります。

金
![]()
は実数です。
実際、例として値を付与すると、
![]()
最初の構造を取得すると、「2×2 直交行列の例」セクションで直交であることが確認された行列が得られます。
![Rendered by QuickLaTeX.com \displaystyle M_1 \left(\theta =\frac{\pi}{2}\right)=\begin{pmatrix} \cos \cfrac{\pi}{2} &\sin \cfrac{\pi}{2} \\[4ex] -\sin \cfrac{\pi}{2} & \cos \cfrac{\pi}{2} \end{pmatrix}=\begin{pmatrix} \vphantom{\frac{\pi}{2}}0 &1 \\[2ex]\vphantom{\frac{\pi}{2}} -1 & 0 \end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1a331cab64745933f7c8a5009c799be6_l3.png)
直交行列のプロパティ
このタイプのマトリックスの特徴は次のとおりです。
- 直交行列は常に反転できるため、特異行列になることはありません。この意味で、直交行列の逆行列は別の直交行列です。
- 任意の直交行列は対角化できます。したがって、直交行列は直交対角化可能であると言います。
- すべての固有値、または直交行列の固有値は、1 に等しい係数を持ちます。
- 実数のみで構成される直交行列も正規行列です。
- 複素数環境における直交行列の類似物は、ユニタリ行列です。
- 明らかに、単位行列は直交行列です。
- n × n 次元の直交行列の集合と行列の積の演算は、直交群と呼ばれる群を形成します。つまり、2 つの直交行列の積は、別の直交行列と等しくなります。
- さらに、直交行列に転置を乗算した結果は、クロネッカー デルタで表すことができます。
![Rendered by QuickLaTeX.com \displaystyle (A\cdot A^{t})_{ij} = \delta_{ij}=\begin{cases}1 & \mbox{si }i = j, \\[2ex] 0 & \mbox{si }i \ne j\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0922008f857f33f46de7551a8ff7cc_l3.png)
- 最後に、直交行列の行列式は常に +1 または -1 です。
![]()
直交行列の解決済み演習
次に、直交行列の練習問題を解きます。
- 次の次数 3 の正方行列が与えられた場合、次の値を求めます。

そして
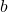
直交させるには:
![Rendered by QuickLaTeX.com \displaystyle A=\frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-892ca58ec5cd36060396cb566902d65d_l3.png)
行列の直交性が満たされるためには、行列の転置による積が恒等行列に等しくなければなりません。それで:
![]()
![Rendered by QuickLaTeX.com \displaystyle \frac{1}{3}\begin{pmatrix}a&a&1\\[1.1ex] b&1&b\\[1.1ex] 1&a&a\end{pmatrix} \cdot \frac{1}{3}\begin{pmatrix}a&b&1\\[1.1ex] a&1&a\\[1.1ex] 1&b&a\end{pmatrix}=\begin{pmatrix}1&0&0\\[1.1ex] 0&1&0\\[1.1ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c2dc9ef8c514302f183ca66626cabc1b_l3.png)
行列を乗算します。
![Rendered by QuickLaTeX.com \displaystyle \frac{1}{9}\begin{pmatrix}2a^2+1&ab+a+b&2a+a^2\\[1.5ex] ab+a+b&2b^2+1&b+a+ab\\[1.5ex] 2a+a^2&b+a+ab&1+2a^2\end{pmatrix} =\begin{pmatrix}1&0&0\\[1.5ex] 0&1&0\\[1.5ex] 0&0&1\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-18a21a22f3cc9747c310d271c3fe4c5c_l3.png)
この位置の要素は一致する必要があるため、行列の左上隅から方程式を取得できます。まだ:
![]()
方程式を解き、未知のものを排除します。
![]()
![]()
![]()
![]()
ただし、右上隅にあるものなど、正の解では成立しない方程式もあります。したがって、否定的な解決策のみが可能です。
一方、変数を計算するには、
![]()
たとえば、最初の列の 2 行目にある用語を照合できます。
![]()
![]()
の値を置き換えることにより、
![]()
方程式では次のようになります。
![]()
![]()
![]()
つまり、考えられる唯一の解決策は次のとおりです。
![]()
したがって、これらの値に対応する直交行列は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle A=\frac{1}{3}\begin{pmatrix}-2&-2&1\\[1.1ex] -2&1&-2\\[1.1ex] 1&-2&-2\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cb7e7a27658da85f7b0d16b17f1f0815_l3.png)
直交行列の応用
直交行列は通常は非常に単純な形式であるため、そうは思わないかもしれませんが、数学、特に線形代数の分野では非常に重要です。
幾何学では、直交行列は実ベクトル空間での等角変換 (距離と角度を変更しない) を表すため、直交変換と呼ばれます。さらに、これらの変換は、考慮されているベクトル空間の内部同型写像です。これらの変換には、回転、鏡面反射、反転などがあります。
最後に、このタイプのマトリックスは剛体の動きを研究できるため、物理学でも使用されます。そして、それらは特定の場の理論の定式化にも使用されます。