垂直または直交ベクトル

このページでは、垂直 (または直交) ベクトルに関するすべてが見つかります。垂直 (または直交) ベクトルとは何か、2 つのベクトルが直交する場合、もう一方のベクトルに垂直なベクトルを見つける方法、垂直ベクトルのプロパティなどです。いくつかの例と、垂直または直交ベクトルの演習問題を解決しました。

2 つの垂直または直交するベクトルとは何ですか?

数学では、2 つのベクトルが互いに直角 (90 度) を形成する場合、それらのベクトルは直交(または直交)します。

次のグラフでは、2 つの垂直ベクトルがわかります。

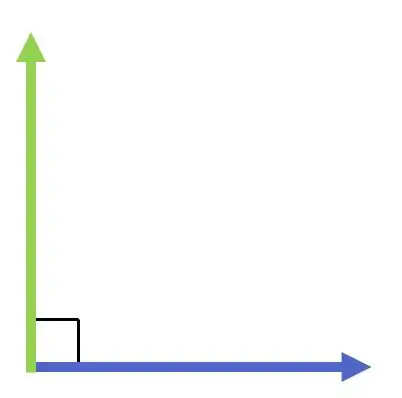
一方、2 つのベクトルの垂直性は、それらの方向にのみ依存し、モジュール (または大きさ) や明らかに方向には依存しません。つまり、2 つのベクトルは、長さが同じかどうかに関係なく、角度が 90 度であれば垂直になります。

2 つのベクトルが直交しているか垂直であるかはどのようにしてわかりますか?

これまで見てきたように、2 つのベクトルが垂直であるかどうかをグラフで確認するのは非常に簡単です。ただし、2 つのベクトルをグラフ化せずに、それらのベクトルが直交しているかどうかを判断することもできます。

数値的には、2 つのベクトルの内積がゼロ (0) の場合、それらのベクトルは直交または垂直になります。

たとえば、次の 2 つのベクトルがグラフ化せずに垂直であることを示します。

$\vv{\text{u}}=(3,2) \qquad\vv{\text{v}}=(-2,3)$

これらが垂直 (または直交) ベクトルであることを確認するには、次のスカラー積公式を適用します。

$\displaystyle \begin{aligned} \vv{\text{u}} \cdot \vv{\text{v}}&=(3,2)\cdot (-2,3) \\[1.5ex]&=3\cdot (-2) + 2 \cdot 3 \\[1.5ex] & = -6+6 \\[1.5ex] & =\bm{0} \end{aligned}$

2 つのベクトルの内積の結果は 0 であるため、これらは互いに直交 (または垂直) する 2 つのベクトルです。

$\vv{\text{u}}\bm{\perp} \vv{\text{v}}$

2 つのベクトルが垂直であることを記号で示していることに注意してください。

$\bm{\perp}}.$

したがって、2 つの垂直ベクトル間の内積はゼロになります。ただし、2 つのベクトルのベクトル積 (ベクトル間の別のタイプの乗算) では、逆の結果が得られます。つまり、他の 2 つのベクトルに垂直なベクトルになります。したがって、2 つのタイプの演算を区別する方法を知ることが重要です。外積のプロパティでそれらの違いを確認できます。

別のベクトルに垂直または直交するベクトルはどのように計算されますか?

平面 (R2) 内で別のベクトルに垂直なベクトルを計算する最も簡単な方法は、ベクトルの 2 つの座標をインターリーブし、符号を 1 に変更することです。

そして、空間 (R3) 内で別のベクトルに垂直なベクトルを取得するには、2 つの座標を相互に挿入し、そのうちの 1 つの符号を変更し、最後に座標を残り 0 に設定する必要があります。

座標が 2 つであるか 3 つであるかに応じて、ある直交ベクトルと別の直交ベクトルの計算の違いを確認できるように、ベクトルの種類ごとに演習を解いてみます。

デカルト平面で垂直または直交ベクトルを見つける

次の 2 次元ベクトルに垂直なベクトルを決定します。

$\vv{\text{v}}=(4,1)$

これは 2 つの成分のみを持つベクトルであるため、垂直ベクトルを取得するには、その成分を交互に配置し、そのうちの 1 つを否定する必要があります。

$\vv{\mathbf{u}}\bm{=(-1,4)}$

内積公式から、これらが実際に垂直ベクトルであることを確認できます。

$\vv{\text{v}} \cdot \vv{\text{u}}=(4,1)\cdot (-1,4) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

デカルト空間内の垂直または直交ベクトルを決定します。

次の 3 次元ベクトルに直交するベクトルを計算します。

$\vv{\text{v}}=(2,3,-1)$

この場合、3 つの成分のベクトルがあるため、垂直ベクトルを取得するには、その成分のうち 2 つを交互に配置し、そのうちの 1 つの符号を変更し、残りの座標を 0 に変換する必要があります。

$\vv{\mathbf{u}}\bm{=(3,-2,0)}$

スカラー積公式を使用して、これらが実際に直交ベクトルであることを確認できます。

$\vv{\text{v}} \cdot \vv{\text{u}}=(2,3,-1)\cdot (3,-2,0) =0$

$\vv{\text{v}}\bm{\perp} \vv{\text{u}}$

垂直ベクトルと直交ベクトルの性質

垂直ベクトルには次の特性があります。

対称関係: ベクトルが別のベクトルに垂直な場合、このベクトルも最初のベクトルに対して垂直になります。

$\vv{\text{u}} \bm{\perp} \vv{\text{v}} \ \longrightarrow \ \vv{\text{v}} \bm{\perp} \vv{\text{u}}$

非反射性: 明らかに、それ自体に対して垂直になるベクトルは存在しません。

$\vv{\text{v}} \ \cancel{\bm{\perp}}} \ \vv{\text{v}}$

ユークリッド幾何学 (R2) では、3 番目のベクトルに垂直なベクトルのペアは必ず平行でなければなりません。つまり、あるベクトルが別のベクトルに垂直であり、そのベクトルが 3 番目のベクトルにも垂直である場合、最初と最後のベクトルは平行になります。これはユークリッドの第 5 公準によるものです。

一方で、これらの特性のおかげでコルク抜きルールが使用できることも知っておく必要があります。この手法を使用すると、このルールがなければ解くのに長い時間がかかるようなタイプのベクトル演算を簡単に計算できます。コルク抜きルールの説明をクリックすると、これが何であるかを確認できます。