既約分数はこれ以上単純化できない分数であるため、これより小さい等価な分数はありません。言い換えれば、既約分数の分子と分母には他に公約数がないため、その gcf は 1 に等しくなります。たとえば、「5/8」という式はもはや約分できないので、それが最も単純な形である、または既約であると言います。
既約分数計算機
理論を続ける前に、任意の混合数の既約分数を求めることができる計算機を紹介します。分子と分母の値を入力し、 「分数を単純化」をクリックするだけで、結果ボックスに縮小された形式が表示されます。このツールを使用して、分数をすぐに単純化したり、分数の練習を修正したりすることをお勧めします。
既約分数とは何ですか?また、どのように計算されますか?
冒頭で説明したように、既約分数はこれ以上単純化できない分数であるため、即分数になります。このタイプの分数を求めたい場合は、 分数の単純化を使用する必要があります。この方法で、最初の分数に関して既約な等価分数を見つけることができます。この最後のリンクでは、分数の簡略化に関する詳細なガイドを見つけることができますが、次のリストでは手順を要約して説明しています。
- 共通因子を見つける:まず、分子と分母の最大公約数を見つける必要があります。このようにして、同等性を維持しながら両方の値を減らすことができる数値を取得します。
- 可約分数を gcf で割る: gcf を取得したら、分子と分母をこの公約数で割る必要があります。これにより、より単純な (またはより小さい) 等価な分子と分母が得られます。
他の方法を使用して既約分数を見つけることもできます。これについては、分数の簡略化に関する記事で説明しています。ただし、これまでに説明したこの方法論を使用すると、必要な端数を非常に簡単かつ迅速に減らすことができます。
可約分数と既約分数の例
次の画像には、約分数の 4 つの例と、さらに 4 つの既約分数の例が示されています。 2 種類の分数の違いを明確に理解するには、それぞれの分数を単純化してみることをお勧めします。
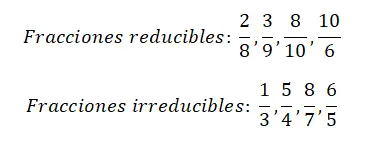
既約分数の計算例
ここでは、2 つの方法を使用して分数を簡略化する方法を段階的に説明します。最初のセクションは、前のセクションで説明した完全な手順を示しています。 2 つ目は、分子と分母を同じ値で除算し、最小の約数 (1 は数えません) から始めて、さらに増やしていく、やや異なるシステムを示しています。ただし、2 番目のシステムが複雑すぎると思われる場合は、無視しても問題ありません。
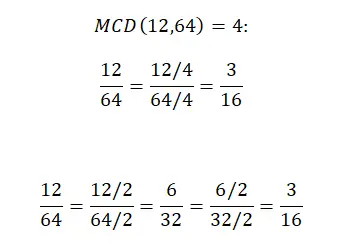
10 進数の既約分数
10 進数から得られる既約分数を母分数といいます。扱う小数の種類 (正確、純粋周期、混合周期) に応じて、異なる方法で計算されることに注意することが重要です。次の例は、この数学的概念を明確に示しています。 5/7 = 0.7142857... ご覧のとおり、7 分の 5 は、10 進数 0.7142857... に相当する既約分数です。
分数が既約かどうかはどうやってわかりますか?
分数が既約か既約かを調べるには、 2 つの方法に従います。 1 つ目は、分子と分母の最大公約数を計算することです。この値が 1 と異なる場合は、それが約分数であることを意味します。そして、その結果として 1 が得られれば、その端数は既約であることがわかります。 2 番目に、最初に示した既約分数計算ツールを使用して、これらの種類のチェックを実行できます。
既約分数の演習問題を解決しました
理論を読んだところで、既約分数の計算を練習できるように、これらの問題を解いてみることをお勧めします。さらに、帯分数の理解を深めたい場合は、これらの分数の練習問題を解いてみることをお勧めします。これにより、分数自体の概念をよりよく理解できるようになります。
演習 1
次の約分数の既約分数を計算します。分数を簡略化するには任意の方法を使用できることを覚えておいてください。演習が終了したら、結果を下の画像に示す結果と比較できます。
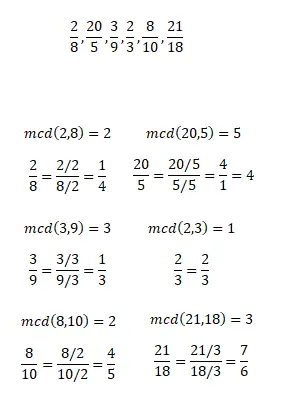
演習 2
既約分数 2/3 と 4/5 に相当する分数を特定します。このタスクを完了するには、分子と分母の数値を確認し、それらの割り切れる関係について考えることをお勧めします。おそらく、最大公約数または最小公倍数を使用して、探しているものを見つけることができます...
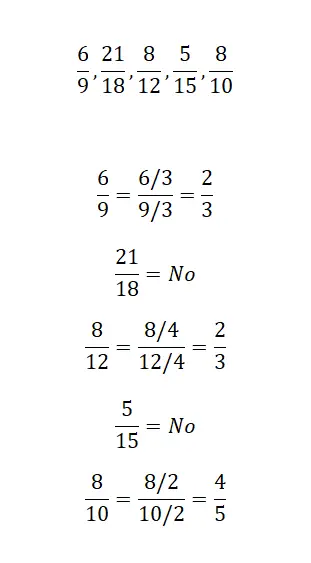
演習 3
この最後の練習では、次の 3 つの分数が同じ既約分数であるかどうかを示すだけで済みます。したがって、3 つの分数をできるだけ減らして結果を分析する必要があります。解決したら、自分のソリューションと当社のソリューションを比較できます。
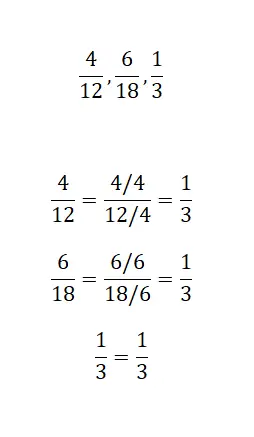
分数についてさらに詳しく
この記事が既約分数の理解に役立つことを願っています。ご質問がございましたら、お気軽に分数の説明をお読みください。そこには、分数に関するすべての情報 (定義、カテゴリ、演算、演習) があり、すべて理論と例を使用して説明されています。この記事を読めば、このトピックに関する多くの根本的な疑問が解消されることを保証します。