2 つ以上の数値の最小公倍数 (LCM) は、これらの数値に共通する最小の (ゼロ以外の) 倍数です。これは、同様の方法を使用して計算されますが、最大公約数の逆演算です。 LCM の計算方法を学びたい場合は、読み続けることをお勧めします。この記事では、一連の数値の最小公倍数を見つけるためのすべての手順 (最も単純な手順から最も複雑な手順まで) を説明します。
lcm計算機
lcm の取得方法について話し始める前に、このページには最小公倍数計算ツールがあることを知っておいてください。これを使用すると、必要なすべての数値の lcm を計算できるようになり、演習の結果を比較して、正しく解けたかどうかを確認できます。
最小公倍数を計算するにはどうすればよいですか?
2 つ以上の数値の最小公倍数を見つけるには、以下で説明する 3 つの方法のいずれかに従う必要があります。次に、選択できるそれぞれの手順を詳しく説明するときに、それぞれの長所と短所についても説明します。こうすることで、問題の LCM を簡単かつ迅速に解決するには、各状況でどれを選択すればよいかがわかります。
方法 1: 複数のリスト
1 つ目の方法は、LCM で計算する数値の倍数のリストを作成することです。次に、すべてのリストで繰り返される最小の値を見つける必要があります。これにより、最小公倍数が得られます。次に、lcm (5, 6) の例でそれを見てみましょう。
5の倍数: 5、10、15、20、25、30、35、40...
6の倍数: 6、12、18、24、30、36、42、48...
最小の共通値を探していますが、lcm はすでにあります。
lcm (5, 6) = 30
方法 2: 階乗分解
次に、数値を因数分解することを選択できます。より具体的には、この方法により、大きな数値の pcm を計算することが容易になります。大きな数の lcm を実行する場合に方法 1 に従うと、倍数の非常に長いリストを記述する必要があるため、時間がかかり退屈になる可能性があります。この 2 番目の手順は、最初は理解するのが少し複雑かもしれませんが、仕組みを理解すると、前の手順と比べて多くの利点があります。そうは言っても、従うべき手順を見てみましょう。
- 階乗分解:最初のステップは、LCM に含めるすべての数値を素因数に分解することです。 数値を階乗分解する方法がわからない場合は、この最後のリンクにアクセスすることをお勧めします。そこでは、数値を迅速かつ効率的に単純化する方法についての一流の説明が見つかります。
- 単一の数式を作成します。すべての数値を素因数で表現したら、最大の指数で累乗した共通の数値と非共通の数値を選択します。次に、それらを 1 つの数式として書き留め、最後に必要な乗算やべき乗を解きます。 lcm の数値はすでに得られています。
方法 3: 数式
最小公倍数を取得する最後の方法は、GCD と次の数式を使用することです。
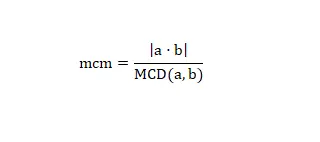
この式を使用すると、任意の数値の lcm を計算できます。実際の例を見てみましょう。 lcm (2.6) を計算したい場合は、(2 x 6) / 2 = 6 という演算を解くだけで済みます。ご覧のとおり、この計算は簡単な方法です。 GCD を持っているか、簡単に計算できる場合は高速です。
lcmを素早く計算するためのヒント
今説明した 3 つの方法をマスターしたら、これから説明する最小公倍数の性質を読むことをお勧めします。これらのおかげで、すでに説明した戦略を使用することなく、LCM を非常に迅速に計算できるいくつかの特定の状況を特定できるようになります。
- 最初の数が 2 番目の数で割り切れる: a が b を割るときの a と b の最小公倍数を計算したい場合、これら 2 つの数の ppcm が最大になります (この場合は b)。たとえば、2 と 8 の lcm を計算する場合、結果は最大となる 8 になります。
- 2 つの素数: 2 つの素数を見つける場合、最も早い方法はそれらを掛け合わせることであり、その結果が ppcm になります。最大公約数が 1 であるため、これは論理的です。つまり、数値を数値そのものよりも単純な因数に分解することはできず、したがって、それらを乗算することしかできないことになります。たとえば、3 と 5 の最小公倍数は、その積の結果、3 x 5 = 15 になります。
分数の最小公倍数を取得するにはどうすればよいですか?
分数の加算または減算を解決するには、最小公倍数を計算する必要があります。これは lcm と同じですが、分数に適用されます。基本的に、合計を 1 つの分数として表現できるように、2 つの分母の lcm を探します。最小公倍数が実分数の計算にどのように適用されるかを確認したい場合は、 このリンクを入力してください。
関数電卓の Lcm
LCM キーは関数電卓にあり、2 つの整数の最小公倍数を計算できます。 Casio 電卓の場合、従う必要がある構文または手順は次のとおりです。まず、 APHA + MCMを押します (この最後のキーには茶色のラベルが付いています)。これが完了すると、両方の数値を入力できますが、数値をカンマ ( SHIFT + , ) で区切る必要があることに注意してください。最後に、等号ボタンをクリックして最小公倍数を取得します。
LCM 演習を段階的に解決
次に、最小公倍数を段階的に解く 3 つの例を示します。このようにして、これらの問題を解決し、この記事で説明したことを少し実践してみることができます。理論を現実に適用する必要があるため、概念を理解したい場合は演習を解くことが重要です。つまり、次の演習で練習できるようにします。
4 と 6 の lcm を計算します。
4の倍数: 4、8、12、16、20、24、28、32、36 ...
6の倍数: 6、12、18、24、30、36、42、48 ...
この演習は、方法 1 (倍数のリスト) を使用して解決します。まず、2 つのリストの共通点を特定する必要があり、小さい方を選択します。したがって、4 と 6 の最小公倍数は12です。
6 と 9 の lcm を計算します。
6の倍数: 6、12、18、24、30、36、42、48 ...
9 の倍数: 9、18、27、36、45、54、63、72 ...
この 2 番目の演習は、前の演習と同じ方法を使用して解決します。まず、2 つのリストのうち最も一般的なものを特定する必要があり、小さい方を選択します。したがって、6 と 9 の最小公倍数は18です。
30 と 40 の lcm を計算します。
30 の素因数分解: 2 x 3 x 5
40 の素因数分解: 2³ x 5
この最後の練習問題を階乗分解法を使って解きます。したがって、最初に 2 つの数値を素因数で表現し、最大の指数で累乗したコモンズと非コモンズを選択する必要があります。したがって、30 と 40 の lcm は2³ x 3 x 5 = 120 となります。